2. Метод Монте-Карло

Монте-Карло! С этим словом обычно связывают игорные дома крохотного княжества Монако, расположенного где-то на юге Франции и состоящего из одного города Монте-Карло.

Почему же вдруг в последнее время слово "Монте-Карло" замелькало на страницах серьезных технических и математических журналов?

Давайте посмотрим поближе, что такое игорная рулетка. Представляет она собой круглое мелкое корытце, внутри которого имеется 100 лунок. В корытце с большой скоростью выпускается легкий шарик, который, многократно отскочив от его краев, останавливается в одной из лунок. Можно ли хоть приближенно предугадать, в какую именно лунку упадет шарик?

Конечно, можно! Если точно определить направление вылета шарика, если точно учесть малейшее дрожание руки бросающего, если точно рассчитать направление отскока при каждом соударении шарика со стенкой корытца, если... Одним словом, если точно знать все условия движения шарика, знать движение всех его молекул, то можно приближенно предсказать место его остановки.

Но совершенно ясно, что учесть точно все факторы, влияющие на движение шарика, никак не удастся. Не удастся еще и потому, что нельзя определить движение его молекул ввиду запрета, накладываемого соотношением неопределенностей, о котором мы уже говорили выше. Да, названных факторов так много и они так быстро и неуловимо меняются, что шарик с равной вероятностью может упасть в любую из лунок, даже если бы не действовало соотношение неопределенностей.

В природе, в технике, в общественной жизни тоже очень часто происходят процессы, носящие вероятностный характер: падение камня с горы, полет птицы, охотящейся за мошкарой, число людей, едущих в поездах, самолетах и трамваях, число банкротств в периоды кризисов капиталистической системы, количество выведенных мальков и количество взрослых рыб, которое сохранится в водоеме, количество детей, которые родятся через 5 или 10 лет. Подобных примеров миллионы. В каждом из них есть элемент неопределенности, в каждом есть вопрос, на который нельзя дать точный ответ. Но ведь многие вопросы такого рода требуют ответа. Например, сколько нужно выпускать самолетов, паровозов, пароходов и трамваев, сколько заводов и какой мощности необходимо строить в ближайшие годы, чтобы обеспечить потребности населения, и каковы будут эти потребности?

Для их решения и применяются вероятностные методы, методы, которые не говорят определенно сколько, но позволяют с достаточной точностью узнать, в каких пределах будет изменяться искомая величина или с какой вероятностью можно ожидать то или иное событие. Один из таких методов и назван методом Монте-Карло.

Чтобы понять сущность его, рассмотрим несложный, но наглядный пример.

Один эксперимент и его математическая модель

Пусть требуется найти площадь круга, радиус которого равен 1 сантиметру. Вычисляется она, как известно, по знакомой еще в школе формуле πr² и равна 3,14·1²=3,14, то есть числу π.

А задумывались ли вы, как, хотя бы приближенно, определить число π?

Методом Монте-Карло это сделать довольно просто. Будем много раз бросать песчинку на лист бумаги, сплошь покрытый окружностями радиусом 1 сантиметр (рис. 42). Песчинка будет падать либо в кружки, либо в пустоты между ними (например, В₁ - положение песчинки в кружке, В₂ - снаружи). Чем больше площадь, занятая кружками, тем чаще песчинка будет в них попадать. Как легко заметить, между площадью кружков и частотой попадания в них песчинки существует прямая связь.

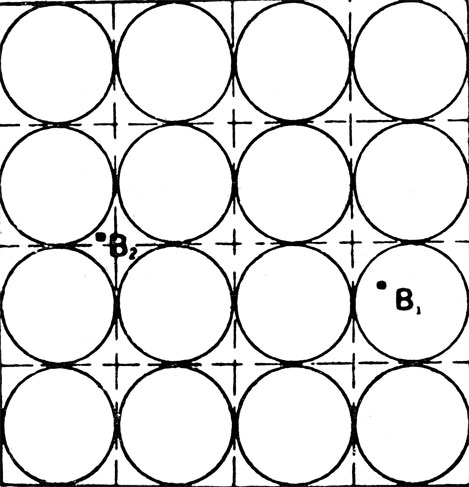
Рис. 42

Пусть вся площадь квадрата, равная 64 см², занята кружками - их будет 16, и пусть из N=1000 бросаний песчинка n=700 раз упадет в кружки и 300 раз на пустоты. Тогда естественно считать, что кружки занимают

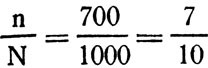
части площади, или 64·0,7=44,8 см².

Разделив полученный результат на 16, мы получим площадь одного кружка, численно равную числу π. Причем результат будет тем точнее, чем большее число раз мы будем бросать песчинку.

Как легко заметить, такой эксперимент займет довольно много времени. Давайте для ускорения работы сделаем математическую модель этого опыта. На рисунке 43 показана часть нашего поля, на которое бросалась песчинка. Ввиду симметрии всего поля вполне достаточно взять часть, равную четверти окружности. Как нетрудно видеть, все наше поле состоит из 64 таких частей. Для моделирования случайного бросания песчинки выберем случайно два числа - А и Б, каждое из которых больше нуля и меньше единицы:

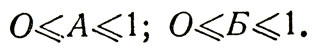
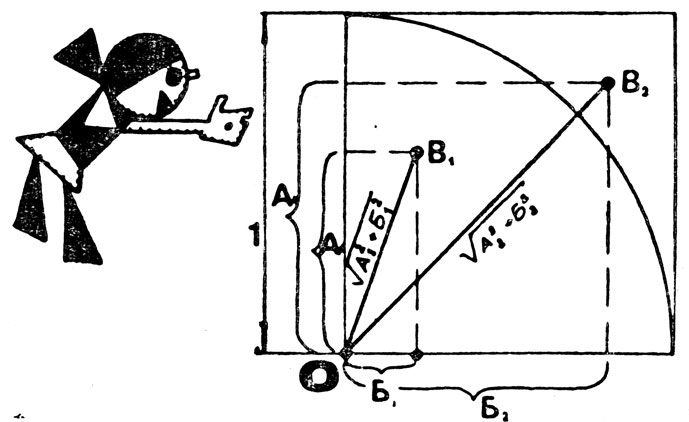
Рис. 43

Откладывая на рисунке 43 от точки О по вертикали числа А, а по горизонтали числа Б, получаем точку В на пересечении перпендикуляров. Например, числа А₁ и Б₁ определяют точку В₁, а числа А₂ и Б₂ - точку В₂. Точки В₁ и В₂ моделируют различные положения песчинки в описанном выше опыте. Если А²+Б²≤1 (меньше или равно), то песчинка расположена внутри окружности или на ней. Если А²+Б²>1 (больше) - она вне его. Таким образом, чтобы знать, попала ли точка В внутрь окружности, достаточно проверить выполнение неравенства А²+Б²≤1.

Теперь можно сопоставить основные моменты эксперимента и его математической модели.

Математическая модель эксперимента

Математическая модель эксперимента готова.

Теперь вместо проведения физического эксперимента (бросания песчинки на расчерченное поле) можно вычислить его результат. Для этого надо иметь лишь таблицу случайных чисел, карандаш и бумагу.

Следовательно, физический эксперимент можно заменить математическим экспериментом - расчетом.

Давайте взвесим возможности обоих способов определения числа π с точки зрения двух факторов: случайных помех и затрат времени на одно и то же число бросании.

Физический эксперимент, как и всякий реальный процесс, в значительной мере подвержен действию случайных помех. Эти помехи проявляются, например, в виде неточности в определении положения песчинки, в виде неровности поверхности поля, что создает определенную тенденцию - песчинки будут "предпочитать" останавливаться во впадинах этого поля. Другим источником неточности будет сам чертеж - неидеальность окружностей и т. д.

Все эти неточности отсутствуют в математическом эксперименте. Правда, говоря уж очень строго, и здесь есть помехи, как-то: ошибки расчета и округления, но их можно сделать очень малыми и пренебречь ими.

Следовательно, с точки зрения погрешностей математический эксперимент предпочтительнее физического.

Теперь о времени. Здесь пальму первенства следует отдать физическому эксперименту. Действительно, расчет на бумаге двух квадратов и их суммы всегда займет больше времени, чем бросание песчинки. Самый неловкий экспериментатор здесь всегда обгонит самого искусного вычислителя.

Но ведь существуют быстродействующие вычислительные машины, которые указанный расчет могут сделать за доли секунды!

Нельзя ли воспользоваться ими для нашего расчета? Попробуем сделать это.

Современная быстродействующая универсальная вычислительная машина без труда справится с этой задачей в кратчайшее время, но... Но для этого следует прежде всего составить программу ее работы. Как человеку-расчетчику нужно указать, что и как считать, так же и вычислительная машина должна "знать", что и как ей считать, иначе она не будет работать. Эту функцию выполняет программа.

Посмотрим, как составляется программа работы вычислительной машины.

Прежде составим программу самого эксперимента. Она показана на рисунке 44. На нем каждый прямоугольник обозначает распоряжение к действию, которое необходимо произвести. Стрелка, выходящая из прямоугольника, показывает, что следует делать при выполнении этого распоряжения. Если из прямоугольника выходят две стрелки, то должно быть указано, в каких случаях движение идет по одной, а в каких - по другой стрелке.

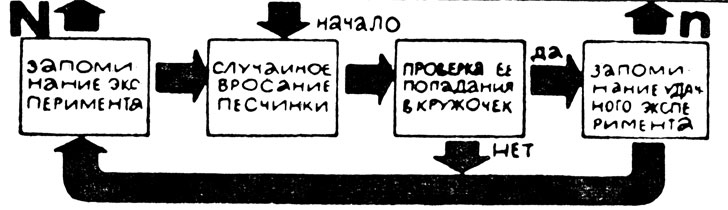
Рис. 44

В схему опыта введены две пустячные операции: запоминание числа экспериментов вообще и удачных экспериментов в частности. Эти очевидные процедуры вводятся потому, что программа должна в точности соответствовать физическому эксперименту. Ведь, бросая песчинку, мы считаем число попаданий в кружки и общее число бросаний. Если их не произвести, то весь эксперимент теряет смысл, так как числа N и n и являются той информацией, которую мы получаем в эксперименте.

Совершенно аналогично составляется программа работы вычислительной машины. Вид программы представлен на рисунке 45. Здесь операциям запоминания в физическом эксперименте соответствуют счетчики (сумматоры) чисел N и n.

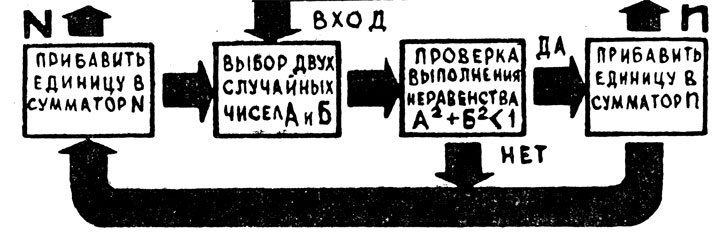
Рис. 45

Внимательно рассматривая обе схемы, мы заметим, что они очень похожи и имеют одинаковую структуру: одинаковое число прямоугольников, а также одинаковое число и направление стрелок, показывающих один и тот же характер связей. Это и неудивительно - обе схемы описывают, по существу, один и тот же информационный процесс определения чисел N и n. Значит, и результат следует ожидать одинаковый: будем ли мы бросать песчинку и определять ее место падения (действовать по программе физического эксперимента) или будем этот эксперимент рассчитывать математически (действовать в соответствии с программой его математической модели).

Таким образом, для получения результата (числа n) в нашем распоряжении имеются два средства: физический эксперимент и расчет по модели этого эксперимента на быстродействующей вычислительной машине. Давайте взвесим все "за" и "против".

Как видно, если не бояться вычислительной машины и иметь возможность обращаться к ней - а сейчас она доступна практически всем, - то преимущество, несомненно, принадлежит расчету, а не эксперименту. Следует все же твердо помнить, что предварительно должна быть составлена математическая модель эксперимента. Только в этом случае можно "разыграть" эксперимент на машине и воспользоваться ее огромным быстродействием для "проведения" большого числа проб, то есть провести математический эксперимент.

Математический эксперимент

Вот такое моделирование физических экспериментов на вычислительных машинах и называется методом Монте-Карло.

Элемент случайности здесь совершенно необходим, поскольку лишь он отражает ту случайность и неопределенность, которая всегда есть в моделируемом физическом эксперименте. В связи с этим метод Монте-Карло часто называют методом статистического (вероятностного) моделирования.

Случайность в машинах специально создается так называемыми датчиками - генераторами - случайных чисел и отражает случайные процессы, происходящие в реальном эксперименте. Такое устройство позволяет вместо громоздкого физического эксперимента строить его удобную математическую модель и многократно "разыгрывать" ее на вычислительной машине.

Моделируемая на машине случайность необходима и полезна. Она отражает вероятностный характер эксперимента и может быть как полезной, так и вредной - быть помехой. В рассмотренном выше эксперименте, позволяющем определить число n при помощи случайных бросаний, случай полезен. А в большинстве других явлений случай проявляется как помеха, которую и приходится моделировать по Монте-Карло с тем, чтобы узнать особенности его влияния и предложить способы для его подавления.

Монте-Карло и баллистические ракеты

Рассмотрим, как мог бы быть применен метод Монте-Карло для расчета точки попадания баллистических ракет.

Траектория полета и точка падения ракеты могут быть очень точно вычислены, если все параметры, влияющие на траекторию ее полета, точно известны. Нужно точно знать вес ракеты и топлива, силу и направление ветра в разных слоях атмосферы на всем пути полета, изменение плотности воздуха, температуры и давления во всех точках, которые ей предстоит пройти, и многое, многое другое.

Но на практике большинство из этих параметров никак нельзя точно определить. Они меняются, причем меняются быстро. Тщательные изучения и наблюдения дали только пределы изменений этих параметров и их статистические свойства. Как же быть?

Для определения точности попадания ракет можно поступить так, как мы поступали в эксперименте с песчинками, - составить программу вычислений траектории движения ракеты. В эту программу входят неизвестные нам параметры. Будем выбирать случайные значения каждого из них в указанных пределах и затем определять точку приземления ракеты. Для другого расчета нужно выбрать другие случайные значения неизвестных параметров, но в тех же пределах и с теми же статистическими свойствами, которые известны заранее из наблюдений, Проделав серию расчетов, получают точки встречи ракеты с землей. Они случайны, так как каждая получена в результате разыгрывания случайного эксперимента. Эти-то точки и определяют так называемый "эллипс рассеяния", который интересует ракетчиков.

Эллипс этот несет чрезвычайно ценную информацию о качестве и эффективности ракеты. По нему можно определить район, где наиболее вероятно ожидать ракету. Размеры его свидетельствуют о точности попадания и т. д.

Как видно, с помощью метода Монте-Карло можно получить весьма ценную информацию о точности попадания ракеты в цель без проведения чрезвычайно дорогих практических запусков ракет и тем самым сэкономить огромные средства.

Весьма своеобразное применение метода Монте-Карло связано с решением некоторых задач математической физики - задач распространения тепла. Поясним это на следующем простом примере.

Пьяный решает задачу

Да, да! И не просто пьяный, а пьяный в стельку, когда ему все равно, по какой пойти дороге, если он стоит на перекрестке. Именно такой, вдрызг пьяный, может помочь решить одну из сложнейших задач математической физики - задачу о распространении тепла в сплошной среде. Вы удивляетесь?

Не торопитесь! Рассмотрим задачу о нагревании пластинки, или, как говорят, плоскую задачу теплопроводности. Такие задачи приходится решать всем, кто имеет дело с оболочками различных нагревательных приборов, таких, как аппараты для сушки волос, головки баллистических ракет, корпуса плавильной печи и т. д. В них всегда очень важно определить поведение температурных напряжений, возникающих в агрегате. Они могут вызвать катастрофу, если слишком велики.

Возьмем для простоты прямоугольную пластинку, края которой находятся под определенной, известной температурой. Задача заключается в том, чтобы вычислить температуру в произвольно выбранной точке пластинки.

У читателя, по-видимому, возникнет недоумение в связи с тем, что здесь явно нет никакой случайности, в то время как выше говорилось, что метод Монте-Карло неразрывно связан со случайными экспериментами. Это недоумение, если оно появилось, совершенно неоправданно, так как законы распространения тепла определяются термодинамикой, которая самым тесным образом связана со статистическими - случайными - процессами.

Известно, что тепло распространяется не непрерывно, а отдельными небольшими порциями, или, как говорят, квантами. Можно считать, что кванты тепла движутся хаотично, в случайных направлениях. Если в выбранной нами точке "собралось" их много, то она, естественно, будет более нагретой по сравнению с той, где таких квантов меньше.

Чтобы узнать, какая в нашей точке температура, нужно определить, как часто в нее "приходят" порции энергии с разных сторон пластинки. Эти порции, начав свое случайное путешествие на одном краю пластинки, заканчивают его на другом. При этом траектория их движения по пластинке совершенно случайна. Нетрудно заметить, что через каждую точку пластинки обязательно пройдут случайные траектории, берущие свое начало на разных кромках пластинки. И температура в этой точке будет равна среднему значению принесенных температур. Например, если через точку проходят траектории, взявшие начало преимущественно на кромке с температурой 50 градусов, то температура в ней будет близка к 50 градусам. Если траектории идут от кромки в 50 градусов и от кромки в 20 градусов - и первых в два раза больше, чем вторых, то температуру точки, как нетрудно догадаться, можно определить простым вычислением:

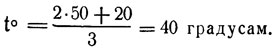
Все рассказанное допускает следующую "алкогольную" интерпретацию, с которой мы начали рассказ.

Представим себе ненадолго, что существует город алкоголиков (автор приносит свои извинения за столь вольное обращение с... представителями этой бравой команды). Пусть он имеет прямоугольную форму, подобную форме нашей пластинки, и все его винные магазины вынесены на окраины; причем каждый магазин узко специализирован и продает вина только заданной крепости. Так, магазин № 40 торгует только "Столичной", № 60 - ромом, а № 12 - сухими грузинскими винами. Допустим еще, что номера магазинов соответствуют температурам кромок той пластинки, о которой говорилось выше, то есть градусы температуры на кромке пластины, градусы крепости напитков в магазинах и номера магазинов на границе нашего выдуманного города совпадают.

Жители этого веселого города, зайдя в магазин, покупают бутылку и начинают с ней свое хмельное и, конечно, случайное путешествие по улицам. Встретившись с другими жителями, которые также запаслись своими бутылками, они делают коктейль, сливая в равных пропорциях содержимое своих бутылок. Крепость полученного коктейля будет нести информацию о том, откуда принесены бутылки и чему равна температура в точке, где этот коктейль распит. Значит, чтобы определить температуру в какой-нибудь точке пластинки, достаточно попробовать коктейль в соответствующем этой точке пункте города алкоголиков.

Однако, наблюдая поведение случайных траекторий, легко заметить, что нашему желанию выпить и определить крепость коктейля будут препятствовать по крайней мере два обстоятельства.

Первое: желая попробовать коктейль на каком-нибудь перекрестке нашего городка, нам придется иногда очень подолгу ждать очередного жителя с бутылкой, так как, бесцельно шатаясь по улицам, он не скоро попадет именно в то место, где мы его ждем.

Более того, большинство их совсем не проходит через точку, где мы ждем и температура которой нас интересует. Поэтому определение температуры подобным образом потребует массы ненужных затрат.

Очевидно, что еще дольше придется ждать, чтобы на нашем перекрестке одновременно встретились несколько жителей и начали делать коктейль (именно это событие нас больше всего интересует). Однако последнее обстоятельство можно преодолеть: не дожидаясь, когда встретятся два и более жителя, собирать дань с каждого проходящего и сливать ее в одну бутылку. Тогда, приложившись к ней, легко определить крепость "ерша" и тем самым оценить температуру в соответствующей точке пластинки.

Но как поступить, чтобы пьяницы почаще выходили на наш перекресток? Подзывать их нельзя - нарушится случайность блужданий. Так как же быть?

Для этого применяют следующий остроумный прием, основанный опять на использовании случайности. Если посмотреть на случайную траекторию, которая обрывается на краях пластинки, то невозможно сказать, где ее начало и где конец. Объясняется это тем, что случайная траектория не зависит от направления движения. Следовательно, можно рассматривать только те траектории, которые выходят из выбранной нами точки, и прослеживать их до пересечения с одной из кромок пластинки, после чего следует "обернуть" движение и считать, что все было наоборот. Тогда эта траектория "принесет" в нашу точку температуру кромки, из которой она "вышла".

А в веселом городе прием этот следует проводить так. Надо взять совсем захмелевшего случайного жителя, пометить его и выпустить из интересующей нас точки города. Продавцов всех винных магазинов при этом попросить сообщить по телефону, в каком магазине помеченный парень закончил свое путешествие. Аналогичную операцию нужно проделать и с другими любителями выпить. Теперь осталось ждать у телефона звонков из магазинов и записывать их номера. Если позвонили из магазинов № 40, 40, 60 и 20, то коктейль в интересующей нас точке имеет крепость

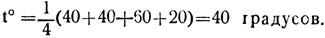
А согласно нашей аналогии такую же температуру имеет и соответствующая точка на пластинке.

Итак, поставленную задачу определения температуры в заданной точке можно решить совсем просто. Надо из этой точки провести несколько случайных траекторий и определить температуру в местах их пересечения с кромкой (напомним, что температура на кромке пластинки задана и считается известной). Тогда температура в выбранной нами точке будет равна среднему арифметическому температур концов случайных траекторий, выходящих из этой точки.

В этом и состоит сущность применения метода Монте-Карло для решения задач по определению температуры.

Где же в нашем примере сама модель явления?

Оказывается, моделировалось движение тепла по пластинке. Ведь направление движения отдельных порций тепла случайно, поэтому мы и модель выбрали такую, в которой имели место случайно перемещающиеся объекты (пьяницы со случайными траекториями движения). Моделирование методом Монте-Карло здесь позволило нам решить поставленную задачу.

Модель пьяницы

До сих пор мы говорили о случайной траектории, прокладываемой пьяным, как о само собой разумеющейся вещи. На то он и пьяный, чтобы случайно плутать по городу.

При решении поставленной задачи на вычислительной машине необходимо уметь моделировать случайные траектории, не обращаясь к услугам алкоголиков. Как это сделать?

Случайные траектории можно прокладывать, например, следующим образом. Возьмем достаточно мелкую прямоугольную сетку и будем двигаться по ее узлам. Начнем из любого узла сетки (это перекресток в городе пьяниц). Выберем одно из четырех направлений: вверх, вниз, вправо и влево - и по нему пойдем.

Поскольку траектория должна быть совершенно случайной, то все четыре возможности должны быть равновероятны. Для выбора направления движения можно воспользоваться простым приемом: бросанием одновременно двух монет. Эти монеты при каждом бросании будут давать один из четырех вариантов: ЦЦ, ЦГ, ГЦ и ГГ, где Ц означает тот факт, что монетка легла вверх цифрой, а Г - вверх гербом. Теперь осталось закодировать эти варианты. Пусть

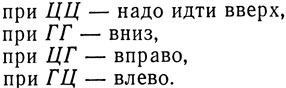
Очевидно, что подбрасывание двух монет дает совершенно случайную команду, после чего мы перемещаемся в следующий узел, совершая часть случайной траектории. Затем снова бросаем монеты, определяя следующее направление движения, и снова делаем шаг случайной траектории в новый узел и т. д. Вся полученная траектория, состоящая из кусочков прямых, параллельных осям решетки, и моделирует случайное блуждание на плоскости.

Подводя итог, заметим, что метод Монте-Карло заключается, по сути дела, в математическом моделировании физических экспериментов, в которых неизбежно присутствует элемент случайности. Многократная постановка физического эксперимента заменяется при этом составлением и многократным "проигрыванием" математической модели данного эксперимента. Значит, вся трудность заключается в составлении модели. И если вам удастся ее сделать, то решить задачу методом Монте-Карло уже не представит большого труда; надо просто запрограммировать и передать ее на быстродействующую вычислительную машину.

Поэтому метод Монте-Карло часто называют методом математического экспериментирования, или методом статистических испытаний, подчеркивая тем самым многократность решения задачи.

В заключение следует отметить, что метод Монте-Карло был создан и получил развитие лишь после того, как появились быстродействующие вычислительные машины. "Ручное" применение метода лишено всякого смысла, так как он связан с большим числом однотипных вычислений.

Как одному человеку, даже самому сильному, не под силу построить пирамиду Хеопса, так в одиночку без вычислительной машины человек не может работать методом Монте-Карло.

Монте-Карло - метод больших скоростных вычислительных машин!