Для точного определения количества информации, которое несет сообщение, К. Шеннон ввел новое понятие - энтропия. Что означает это слово?

Первую количественную меру информации ввел Р. Хартли. Но эта мера охватывала только частные случаи, когда все сообщения или их элементы встречаются одинаково часто. К. Шеннон подметил, что в большинстве случаев и биты разного качества, и буквы, и слова встречаются в сообщениях с разной вероятностью: одни чаще, другие реже. Для учета этого явления К. Шеннон ввел новое понятие - энтропия. Что означает это таинственное слово?

Предположим, вы работаете в конструкторском бюро в составе небольшой группы из четырех сотрудников и начальника. Последний для удобства вызова к себе подчиненных применил простейшую систему связи: мелодично звенит звонок, и на табло загорается одна из четырех лампочек, на которых нарисованы первые буквы фамилий сотрудников. Вот они: "И" (Иванов), "П" (Петров), "С" (Сидоров), "Д" (Добров). Пусть ваш код "Д".

Первые месяцы шла дружная коллективная работа над проектом с равным участием каждого, и шеф одинаково часто зажигал все четыре лампочки, приглашая то "И", то "П", то "С", то "Д" для консультаций. Царила отличная творческая атмосфера "равенства и братства". Так как использовались сигналы четырех качеств, то вспышка одной лампочки, как мы уже твердо знаем, несла 2 бита информации (log 4 - выбор решения из четырех возможных исходов). Вероятность вспышки вашей лампочки или любой из них (строго говоря, это не вероятность, а частота события) есть отношение

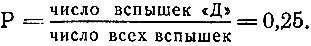
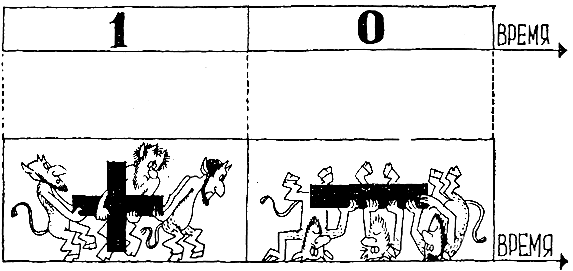
Но вот вы предложили оригинальное решение основного узла проекта. Шеф увлекся этой идеей; почти все время загоралась только лампа "Д". Как только раздавался звонок, вышли на зов, лишь изредка проверяя себя по лампочке. Учет вспышек показал, что вероятность вашего светового кода стала Р = 0,97, а три других вспыхивали с вероятностью Р = 0,01 каждая. (Сумма этих вероятностей, очевидно, всегда равна единице: 0,97 + 0,01 + 0,01 + 0,01 = 1.)

Легко видеть, что чем больше равновероятных сигналов или кодов используется, тем меньше вероятность каждого из них. Если бы в группе было 10 сотрудников и 10 лампочек, то вероятность загорания любой из них была бы уже не 0,25, а 0,1.

К. Шеннон показал, что и при равновероятных, и при неравновероятных сигналах количество информации в посылке или коде определяется вероятностью его появления. И зависимость эта. обратная: чем чаще появляется данный код, тем меньше информации он несет. Вот почему вы почти не контролировали себя по "лампочке, а сразу шли к шефу, хотя из 100 вспышек только 97 были ваши. Вспышка лампы "Д" была почти достоверной. А количество информации в ее вспышках катастрофически уменьшилось: она составила log 1/0,97 - 0,000001 бита. Но зато информация в редких посылках ламп "И", "П" и "С" резко возросла: log 1/0,01 - 3,32 бита.

Это хорошо иллюстрирует лотерея. Некто проверяет по выигрышной таблице свои билеты: один, другой, третий... десятый - все пусто. Он уже и не ждет выигрыша; каждый очередной билет несет ту же унылую информацию и не вызывает эмоций. Но вот он подпрыгнул, просиял, заметался, покрылся испариной... Это все сделал гигантский залп информационной "пушки": он выиграл автомобиль, и не какой-нибудь, а "Волгу". Если, допустим, имеется всего один такой выигрыш на миллион билетов, то, естественно, беднягу потряс мгновенный информационный удар в log 1/0,000001 = 20 бит! Говорят, что некоторые со слабыми нервами просто не выдерживают такого удара.

Но вернемся в КБ. Прошло некоторое время, и ситуация резко изменилась. Начальник решил не применять вашу находку ("Идея хорошая, но не проверена. А вдруг наткнемся на подводные камни и пойдем ко дну? У нас жесткие сроки. Я не могу рисковать. Проедем еще на старом; хуже, но надежно".) Вы начали упорствовать, искать поддержку. Это вконец испортило отношения. Постепенно вспышки "Д" замерли, старую работу вы кончили, новой не предлагали. Стало тоскливо. На лампы вы уже не смотрите, а чтобы чужие звонки не мешали грустным мыслям, ватой затыкаете уши...

И вот в такой ситуации вспышка лампы с кодом "Д", конечно, несла бы огромную информацию: "увольнение", "принятие предложения", "пас в сторону" - в другой отдел и т. д. И лампа "Д" наконец вспыхивает. Вы не замечаете. Коллеги толкают вас, вы спешите к шефу...

Как же меняется общее количество информации, которое несет табло из четырех лампочек при описанных перипетиях в нашем условном КБ?

К. Шеннон дал общий рецепт: надо вычислить информацию, сообщаемую каждым кодом (у нас каждой лампой), и усреднить по всем кодам (по всем лампам). Только усреднять надо не обычно, а по законам случайных величин: информацию, сообщаемую каждым кодом, умножать на вероятность его. появления и складывать полученные величины.

Проделав это, мы получим знаменитую формулу К. Шеннона для вычисления средней информации, сообщаемой данным набором сигналов. Эту величину К. Шеннон и назвал энтропией, и обозначил буквой Н:

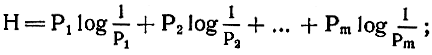
где Р₁, Р₂... Р_m - вероятности появления кодов, a m - общее число кодов.

Обозначив в нашем случае вероятности вспышек ламп Р_и (Иванов), Р_п (Петров), Р_с (Сидоров) и Р_д (Добров) для ситуации появления новой идеи, полутаем

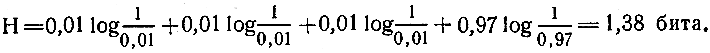
Легко видеть, что в период "равенства и братства" в КБ, когда Р_и = Р_п = Р_с = Р_д, формула К. Шеннона переходит в формулу Р. Хартли Н = J = log 4 = 2 бита.

Таким образом, неравновероятное вспыхивание лампочек привело к уменьшению информации, сообщаемой световым табло, к уменьшению энтропии.

При каком же распределении вероятностей между кодами будет передаваться максимальная информация 1 или энтропия достигнет своего максимума?

Исследование формулы К. Шеннона дает однозначный ответ - это имеет место при равной вероятности появления используемых кодов, слов, букв, вспышек.

В этом случае имеет место наибольшая неопределенность для адресата (одинаково часто загорается любая лампа), и общее количество передаваемой информации достигает максимума.

Отсюда следует важный практический вывод: наибольшая скорость передачи информации (телеграмм, команд, знаков) будет тогда, когда имеет место равновероятная ситуация.

Для приближения к ней применяют специальные преобразователи, которые выравнивают вероятности появления элементов используемого алфавита.

Далее К. Шеннон показал, что наибольшей энтропией обладают сигналы, имеющие форму... шума! Это звучит парадоксом. Ведь шум - это те самые черти, которые признают только хаос и стараются разрушить, уничтожить, искромсать любую информацию. Как же можно шум заставить нести информацию, как его запрячь в коляску битов, в коляску нулей и единиц? Ведь у шума все меняется. Амплитуда, частота и фаза одного куска шума и другого совершенно непохожи.

Но есть у этих вездесущих и непрерывно меняющихся чертей один устойчивый параметр, который даже они не в состоянии изменить - это закон их хаоса. В частности, интересующие нас шумы типа тепловых подчинены закону Гаусса. Есть и другие типы шумов, подчиненные другим законам. Как же себе представить передачу информации с помощью шума?

А вот как. Пусть канал, имеющийся в нашем распоряжении, работает двоичными сигналами, то есть по нему передается информация с помощью нулей и единиц. Записываем кусок шума (например, на магнитофонную ленту) и будем передавать его вместо 1. Для передачи О тот же образец шума (его принято называть "реализацией шума") опрокидываем вверх тормашками: эта операция соответствует его умножению на минус 1, и тоже передаем.

А как поступать на приеме; как отличить посланные шумовые сигналы от естественных шумов?

Здесь-то и помогают нам законы хаоса. Если нашу выбранную для передачи "реализацию шума" заранее "сообщить" приемнику, то он будет сравнивать приходящие шумовые нули и единицы с образцом и правильно восстанавливать передаваемую информацию.

Практически, чтобы упростить систему и исключить "перевозку" образца хаоса на прием, человек нашел способ создавать совершенно одинаковый хаос и на передаче, и на приеме.

Этот искусственный хаос уже не совсем шум, а псевдошум и вполне подвластен нам. На передаче и на приеме ставятся такие генераторы, которые генерируют одинаковый псевдошум. При передаче 1 приходящий и местный псевдошумы должны быть одинаковы, а при передаче 0 - приходящий перевернут с ног на голову.

Какой же все-таки резон заменять нашу стройную, правильно очерченную посылку-сигнал куском шума, "псевдошума", то есть десятком беснующихся чертей-помех? Ведь тогда придется при том же числе битов информации расширить в десятки раз полосу пропускания канала связи или при той же полосе в десятки раз снизить скорость передачи?

Верно. Но зато шумовой сигнал позволяет создать ряд новых удивительных систем связи. Вот один только пример.

"Набивая" все больше и больше псевдочертей в посылку, что требует все большего расширения занимаемой полосы частот, мы можем сделать их в десятки и сотни раз меньше "ростом", чем естественный шум приемника. Тем самым мы замаскируем сигнал под шумы,

Но тот приемник, который знает их реализацию, сразу распознает их, соберет всех, распыленных в гигантской полосе, воедино и восстановит передаваемую ин формацию. Этот процесс называют "сверткой шумового сигнала".

Однако не только скрытностью знамениты эти карлики - наши псевдочерти. Их так много, что безболезненно для информации можем "хирургически" удалять значительную их часть (больше половины).

Такая ампутация требуется в том случае, когда на какую-то часть карликов наваливается сильная помеха, например соседняя радиостанция. Делает ее приемник, который автоматически замечает помеху и вырезает и помеху и поврежденных карликов.

Когда мы впервые стали проверять эту удивительную живучесть псевдошума, то у многих были сомнения в пригодности метода. Гигантские помехи наседали на наших карликов то тут, то там в спектре сигнала, но их спокойно вырезали фильтры-выключатели, а информация продолжала идти без искажений.

Такие системы с шумоподобными сигналами в различных модификациях уже нашли практическое применение. В частности, они дали возможность разобраться в "каше" из ряда копий сигнала, поступающих в приемник с запаздыванием во времени (многолучевое распространение радиоволн), о которой мы говорили в начале главы.

Вот к каким интересным результатам привело нас понятие энтропии.