Расчленение нестандартного вопроса

В случае n-ричного вопроса все п возможных вариантов ответа можно заранее предусмотреть и перенумеровать числами от нуля до n-1 [нулевой вариант, первый, второй, третий и т. д. до (n-1)-го]. Поэтому в дальнейшем можно ограничиться рассмотрением только вопросов с числовыми ответами.

Пусть, например, мы имеем восьмеричный вопрос с вариантами ответа 0, 1, 2, 3, 4, 5, 6, 7. Покажем, что этот вопрос может быть заменен равносильной ему серией из трех двоичных вопросов. Для этого расположим все варианты ответа вдоль отрезка прямой линии (рис. 3). Разделим сперва весь отрезок пополам, затем каждую половину на две четверти и каждую четверть на две восьмушки. Зададим теперь один за другим три двоичных вопроса:

1) Находится ли число, изображающее нужный вариант ответа, в правой половине отрезка?

2) Находится ли оно в правой четверти только что указанной половины отрезка?

3) Находится ли оно в правой восьмушке соответствующей четверти?

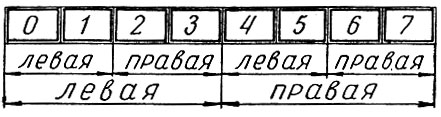
Рис. 3. Как угадать цифру по трем вопросам

Совокупность трех ответов определит нам требуемое число однозначно (например, "да, да, нет" означает число 6; "нет, да, нет"- число 2). На этом основании один восьмеричный вопрос считают эквивалентным (равноценным) трем двоичным. Если принять, что ответ на один двоичный вопрос дает единицу информации, то ответу на восьмеричный вопрос следует приписать три таких единицы.

Такой же прием оценки количества информации можно применить и в случае любого n-ричного вопроса, если n представляет собой целую степень двух:

Следовательно, двоичный ответ содержит одну единицу информации, четверичный (эквивалентный двум двоичным) - две единицы, восьмеричный - три, 16-ричный - четыре, 32-ричный - пять единиц и т. д. Как видим, количество информации q в n-ричном ответе равно показателю той степени, в которую нужно возвести два, чтобы получить n, то есть логарифму числа n при основании 2

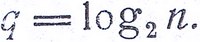
По соображениям непрерывности эта формула остается справедливой и тогда, когда п не является целой степенью двух.