В поисках лаконичной записи

Носитель можно представлять себе состоящим из множества отдельных элементарных участков, на каждом из которых может быть запечатлен тот или иной знак. На элементарном участке бумаги может быть отпечатана одна из 32 букв русского алфавита, участок фотографии может стать черным, серым или же белым, участок магнитофонной ленты может быть намагничен в той "ли иной степени.

Иногда требуется записать русский текст на перфокарте-разграфленном куске картона, в каждой клетке -которого можно только пробить (или же не пробить) стандартное круглое отверстие. Два возможных состояния каждой клетки (пробита или же не пробита) соответствуют двум вариантам двоичного ответа. Поэтому каждая клетка вмещает ровно одну единицу информации. Следовательно, для записи одной из 32 русских букв, несущей пять единиц информации (log₂ 32 = 5), требуется пять клеток. И действительно, существует как раз 32 способа пробить отверстия в группе из пяти клеток, так что каждая из комбинаций может быть сопоставлена одной из букв. На рис. 4 показано такое сопоставление, похожее на используемый в телеграфии "код Бодо" ¹.

¹ (В отличие от рис. 4 в коде Бодо буквы э, щ, й изображаются иначе (на цифровом регистре), а соответствующие комбинации отверстий используются для изображения пробела между словами и переводов регистра.)

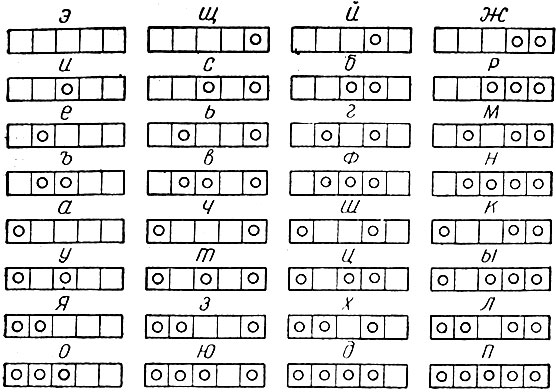
Рис. 4. Телеграфная азбука Бодо

Рассмотрим другой пример. Имеется возможность печатать на бумаге буквы русского алфавита, записать же нужно длинную последовательность цифр. Можно, конечно, изображать цифры словами, например, "восемь", "шесть", "нуль". Но это было бы крайне неэкономно. Гораздо лучше условно обозначить каждую цифру буквой, скажем, единицу - А, двойку - Б и т. д. Но и этот способ - не самый выгодный, так как из всего многообразия букв используется лишь десять.

Из 32 букв можно составить 1024 (т. е. 32²) двубуквенных сочетания, а каждому из них сопоставить одно из тысячи трехзначных чисел от нуля до 999. Сделать это можно, например, так:

Таким образом, разумно используя многообразие алфавита, можно с помощью одной пары букв изображать три цифры, расходуя в среднем две трети буквы для записи одной цифры. По сравнению с предыдущим способом это дает экономию места при записи в полтора раза. При этом естественная емкость носителя используется почти полностью, так как остаются без употребления только 23 двубуквенных сочетания, которым соответствуют числовые значения больше 999 (в нашей таблице такие сочетания взяты в скобки). Дальнейшее усовершенствование методов записи (например, использование многобуквенных сочетаний) существенной экономии дать не может.

Но можно ли указать общий рецепт, который позволял бы находить такие наивыгоднейшие способы записи во всех случаях, не требуя каждый раз особенного остроумия и догадки? Оказывается, такой рецепт есть, но чтобы понять его, нужно на время вообразить себя учеником третьего класса, изучающим основы нумерации.