Нумерация и хранение информации

Какое же отношение имеют различные системы нумерации к проблемам хранения информации? А самое непосредственное! Ведь каждое сообщение слагается из элементов, а каждый элемент имеет п вариантов (если элемент- буква, то n=32, если же цифра, то n=10, а если точка телевизионного кадра, то n = 8). Все варианты каждого элемента сообщения можно перенумеровать целыми числами от 0 до n-1. При хранении информации вместо самих элементов сообщения достаточно записать соответствующие номера, так что все сообщение в целом будет заменено некоторой последовательностью цифр, каждая: из которых может иметь любое значение от нуля до n-1 Но ведь это - не что иное, как запись некоторого многозначного числа К в n-ричной системе нумерации!

Предположим, что система хранения информации такова, что каждый элемент носителя может находиться в m различных состояниях (то есть на каждом элементе носителя мы можем нанести любой из т определенных "знаков"). Если m совпадает с n, то проблема записи очень проста: каждый вариант элемента сообщения изображается одним из вариантов знака. Если же m отличается от n, то число К, соответствующее сообщению, нужно предварительно преобразовать из n-ричной системы нумерации в m-ричную, после чего запись его посредством m состояний носителя трудностей не представляет.

Обозначая трехзначные числа парами русских букв, мы, по сути дела, записывали их в 32-ричной системе нумерации (только начертание "цифр" было не совсем обычным: нуль - А, единица - Б и т. д.).

Если отверстие в перфокарте рассматривать как обозначение единицы, а отсутствие отверстия - как нуль, то приведенный ранее код Бодо ставит в соответствие каждой букве русского алфавита некоторое число от 0 до 31, выраженное в двоичной системе. Такое же соответствие между буквами и цифрами используется при осуществлении автоматического перевода литературы на электронных вычислительных машинах.

Переход от одной системы нумерации к другой позволяет приспособить информацию для записи на любом носителе любыми знаками. Всего выгоднее тот способ записи, который позволяет зафиксировать на данном носителе наибольшее количество информации. Один знак-буква вмещает в пять раз больше информации, чем один знак-отверстие. Но отверстие (или точка) занимает на носителе во много раз меньше места, чем буква. Если за единицу площади принять самый маленький квадратик, на которОхМ только можно записать четко воспринимаемую точку, то для изображения буквы потребуется занять - в среднем - десятка два таких квадратиков (рис. 5). А для обозначения той же буквы в двоичной системе достаточно пяти квадратиков!

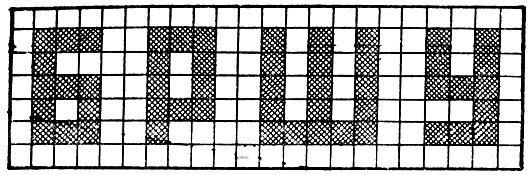
Рис. 5. Обычные буквы неэкономны

Это только один из многочисленных примеров, иллюстрирующих экономичность двоичной записи. В качестве второго примера сравним двоичную нумерацию с десятичной. Попробуем "записывать" цифры десятичной системы на перфокарте: единицу - одним отверстием, двойку - двумя отверстиями, тройку - тремя и т. д. Тогда для записи каждой цифры многозначного десятичного числа нужно предусмотреть девять клеток (ведь эта, заранее неизвестная, цифра может оказаться девяткой!). Тогда для записи любого трехзначного числа нужно располагать 27 клетками. При двоичной же записи любое число от 0 до 1023 может быть обозначено двоичным десятиразрядным числом (число 1024=2¹⁰ представляет собой уже единицу одиннадцатого разряда). Так как любая двоичная цифра (0 или 1) может быть записана в одной клетке, для двоичной записи любого числа от 0 до 1023 достаточно десяти клеток. Как видим, это почти втрое экономичнее, чем при десятичной нумерации. Сдру. гими преимуществами двоичной нумерации мы еще встретимся в дальнейшем.