4.1. Комбинации высказываний

Два любых высказывания можно объединить в одно с помощью двух основных операций: конъюнкции - логического И, обозначаемого AND, и дизъюнкции - логического ИЛИ, обозначаемого OR. Так, например, высказывания "Вчера было пасмурно" и "Сегодня утром шел снег" можно связать конъюнкцией и получить высказывание "Вчера было пасмурно и сегодня утром шел снег". Из тех же высказываний с помощью дизъюнкции можно получить следующее: "Вчера было пасмурно или сегодня утром шел снег". Высказывание, полученное с помощью конъюнкции, принимает значение истина только тогда, когда значения обоих входящих в него высказываний истинны. Во всех остальных случаях конъюнкция ложна. Дизъюнкция принимает значение лжи только тогда, когда оба входящих в нее высказывания ложны. В остальных случаях дизъюнкция равна истине.

В логике используется также другая операция, напоминающая дизъюнкцию, которая называется ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR). Высказывание, получаемое с помощью данной операции, принимает значение истина при условии, что одно, и только одно, из входящих в него высказываний имеет значение истины. В разговорной речи такие высказывания часто объединяются конструкцией "или ..., или ...", например: "Или я пойду на футбольный матч, или будут смотреть его прямую трансляцию по телевизору". Очевидно, что истинность одной составляющей исключает истинность другой.

Другая важная операция, используемая в логике,- это отрицание, логическое НЕ, обозначаемое NOT. Например, из высказывания "Сегодня идет снег" можно с помощью отрицания получить "Сегодня не идет снег". Представление значений сложных высказываний для каждой возможной комбинации значений их составляющих осуществляется с помощью так называемых таблиц истинности. Например, в табл. 4.1 одновременно представлены четыре таблицы истинности для операций И (AND), ИЛИ (OR), исключающее ИЛИ (XOR) и НЕ (NOT). В данной таблице буквами Р и Q обозначаются любые два логических высказывания.

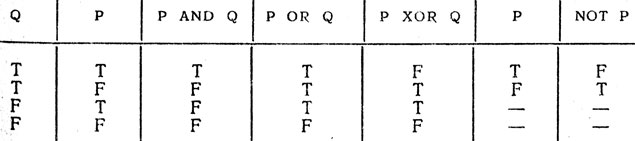
Таблица 4.1

Рассмотрим логические функции, представленные в табл. 4.2.

Таблица 4.2

Как видно из табл. 4.2, высказывание Р AND NOT P (Р И НЕ Р) всегда принимает значение ложь, тогда как высказывание Р OR NOT Р (Р ИЛИ НЕ Р), наоборот, всегда имеет значение истина. Высказывание, всегда имеющее значение истина, называется тавтологией. Высказывание с постоянным значением ложь называется противоречием. Читатель может самостоятельно проверить, что высказывание, составленное с помощью операции XOR из высказываний Р и NOT P, представляет собой тавтологию. Другим не менее полезным упражнением будет сравнение таблиц истинности для высказываний Р XOR Q и Р AND NOT Q OR NOT P AND Q. Заметим, что следует учитывать приоритеты логических операций: сначала выполняется отрицание (NOT), затем конъюнкция (AND) и, наконец, дизъюнкция (OR). Изменить порядок выполнения операций можно с помощью скобок: действия в скобках производятся в первую очередь. В том, что результат зависит от порядка выполнения операций, можно убедиться, сравнив, например, таблицы истинности для высказываний NOT P AND Q и NOT (P AND Q).

В заключение данного раздела еще раз напомним, что хотя все логические высказывания - это обычные предложения есте- o ственного разговорного языка, обратное не всегда верно, т. е. не все предложения естественного языка могут служить логическими высказываниями. Приведем еще один пример. О фразе "Это предложение ложно" нельзя сказать, что она имеет значение истина или ложь. Следовательно, данная фраза не является логическим высказыванием.