4.3. Логическое следование (импликация)

Рассмотрим высказывания типа "Если Р, то Q". Частным случаем высказывания данного типа служит, например, следующее: "Если дождь идет, то трава растет". В приведенном примере Р - "идет дождь", a Q - "трава растет". Следует отметить, что таблица истинности для этого высказывания должна включать в себя его значения для всех комбинаций значений составляющих. Т. е. истинность высказывания типа "Если Р, то Q" зависит от того, как интерпретируются значения Р и Q. Например, можно обнаружить, что значение всего высказывания - ложь, когда значение Р равно истине, a Q - лжи, что для приведенного выше примера соответствует тому факту, что при дожде трава не растет.

Итак, мы имеем три логические величины: само высказывание и две его составляющие. Каждая из этих величин может произвольно принимать значение истина или ложь. Дождь может идти и не идти, трава может расти и не расти и, наконец, истина или ложь может заключаться в суждении, что если идет дождь, то непременно растет трава. В логике нет ничего, что могло бы нас убедить в истинности высказываний типа "Если Р, то Q". Проверить его истинность можно только на практике, исходя из сведений о реальном мире. Мы можем, например, обнаружить, что данное высказывание принимает значение ложь при условии, что Р истинно, a Q ложно. Для приведенного примера это соответствует ложности суждения, что когда идет дождь, трава не вырастет. Можно убедиться, что для всех других комбинаций значений Р и Q приведенное высказывание имеет значение истина.

Для начинающих изучение логики очень важно понять, что ее цель не столько проверка правильности произвольных суждений о реальном мире, сколько дедуктивный вывод значения одних высказываний из других. По высказыванию "Если Р, то Q" в случае, когда Р ложно, нельзя судить об истинности Q. В приведенном примере этот случай соответствует тому, что если дождь не идет, трава может расти и не расти - и то, и другое может быть истиной. Поэтому для рассмотренного случая, т. е. при условии, что Р принимает значение ложь и при любом значении Q, все высказывание остается истинным. Однако, если данное высказывание истинно, то из истинности Р необходимо следует истинность Q.

Операция, соответствующая высказываниям типа "Если Р, то Q", называется логическим следованием, или импликацией, и обозначается Р IMPLIES Q.

В логике есть другая операция, напоминающая импликацию и задаваемая высказываниями "Р тогда и только тогда, когда Q" или "Для Р необходимо и достаточно Q". Эта операция называется логическим тождеством и обозначается IFF.

Таблицы истинности для обеих рассмотренных операций представлены в табл. 4.4.

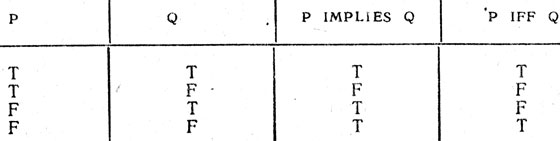
Таблица 4.4