4.11. Пролог и цифровые логические устройства
Для того чтобы разобраться в описываемом ниже применении Пролога для построения электронных схем, реализующих логические функции, не нужно быть специалистом в электронике. Достаточно знать, что логические схемы представляют собой разновидность электронных схем, имеющих один или несколько входов и один выход. Сигналы на выходе схемы зависят от различных комбинаций электрических потенциалов двух уровней, подаваемых на ее вход. Логические уровни, которые раньше задавались с помощью значений истина и ложь, определяются в логических схемах как уровни электрических потенциалов на входах и выходах этих схем.
Схемы, в которых более высокий уровень напряжения соответствует логической единице (истине), а низкий - логическому нулю (лжи), называют положительными логическими схемами. На выходе элементарной логической схемы (вентиля) устанавливается сигнал, соответствующий значению истина или ложь в зависимости от комбинации логических сигналов на входе. Из элементарных схем строятся более сложные. Примеры таких элехментарных схем, реализующих функции AND, OR, NOT, NAND и NOR, представлены на рис. 4.1.
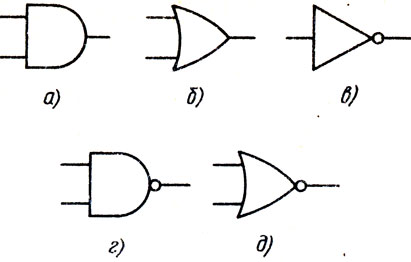
Рис. 4.1. Символические обозначения логических элементов: а - AND, б - OR, и - NOT, г - NAND, д - NOR
Все эти вентили, кроме одновходового инвертора (схема NOT), имеют по два входа. В программе 4.9 используется отношение fn, моделирующее работу схем NOT и AND. Преимущество предлагаемого метода заключается в простоте представления сложных схем. Чтобы обозначения вентилей отличались от имен встроенных отношений Пролога, в программе для отношений, моделирующих элементы схем, используются имена, состоящие из первой большой буквы и остальных малых, например And, Not и т. д.
(Not 0) fn 1
(Not 1) fn 0
(And 0 | X) fn 0
(And 1) fn 1
(And 1 | X) fn Y if
(And | X) fn Y
Ниже приводится пример работш этой программы:
all (xyz: (And xy) fn z)
0 X 0
1 0 0
1 1 1
No (more) answers
Работа трехвходового элемента And моделируется с помощью запроса
Результат всегда помещается в последнем столбце.
Упражнение 4.7
Написать программу, моделирующую работу вентиля Оr, а затем с помощью отношения Not, а также отношений And и Оr определить отношения Nand и Nor.
Приведенная ниже программа 4.10, построенная с помощью отношений tab и b, позволяет выводить на экран таблицы, описывающие зависимости выходных сигналов от входных для произвольных логических схем. Отношение tab выводит списки уровней входных и выходных сигналов, тогда как отношение b обеспечивает генерацию всех двоичных последовательностей, имеющих длину, соответствующую числу входных сигналов.
(X) b 1 if
X ON (∅1)
X b Y if
1 LESS Y and
SUM(1 Z Y)and
x b 1 and
у b Z and
APPEND (x у X)
tab(X Y Z x)if
Z b X and
fn((Y|Z)x)
В отношении tab переменная Y обозначает название схемы, X - число входов, Z - комбинацию нулей и единиц, обозначающих уровни входных сигналов, ах - уровень выходного сигнала. Например, для получения таблицы зависимости выходного сигнала от входов схемы Nand (с помощью отношения из ответа к упражнению 4.7) необходим следующий запрос:
all (х у): tab (3 Nand x у)
(0 0 0) 1
(0 0 1) 1
... и т. д.
(1 1 1) 0
Теперь определим отношение, позволяющее анализировать работу сложной логической схемы. На рис. 4.2 представлена Довольно простая логическая схема, имеющая два уровня, на первом из которых расположены два входных элемента: первый - And с двумя входами, другой - Or с тремя. На втором, выходном уровне размещен один элемент NancL Ниже приводится определение отношения com, позволяющего описывать работу таких схем:
(X Y Z х у) com z if
tab (X Z X1 Y1) and
tab (Y x Z1 x1) and
APPEND (x1 z1 y1) and
(y Y1 X1) fn z1 and
APPEND (y1 (z1) z)
В приведенном выше фрагменте программы таблицы уровней входных и выходных сигналов получаются с помощью отношения tab. Затем совокупность сигналов первого уровня используется для моделирования работы второго уровня схемы с помощью отношения fn и списка значений входных сигналов z. Окончательный ответ обеспечивается оператором Пролога APPEND. Так, для схемы, показанной на рис. 4.2, таблица может быть получена следующим образом:
all (X: (2 3 And Or Nand) com x)
(000001)
(000011)
... и т. д.
(11110 0)
(111110)
No (more) answers
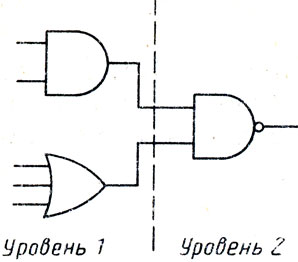
Рис. 4.2. Двухуровневая логическая схема
Отметим, что первые две переменные используются для обозначения числа входов двух элементов первого уровня. Элемент второго уровня был уже описан ранее и имеет два входа.
Упражнение 4.8
Напишите запросы, позволяющие получать таблицы истинности логических схем, имеющих структуру:
а) два двухвходовых элемента Nand, соединенные на выходе с Nor;
б) два двухвходовых элемента And, соединенные на выходе с таким же And;
в) два инвертора (Not), соединенные с элементом Nand.
Упражнение 4.9
а. Сравните результаты выполнения упражнений 4.8, а и б.
б. С помощью отношения fn получите таблицу истинности для двухвходового элемента Or и сравните результат с ответом в упражнении 4.8, в.
|
ПОИСК:
|
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'