4.12. Использование логических элементов для доказательства теорем
Упражнения 4.8 и 4.9 должны были подготовить читателя к изучению материала данного раздела. Отношения, описанные выше, могут быть использованы для доказательства теорем логики и булевой алгебры. Например, рассмотрим два частных случая применения одного из правил де Моргана:
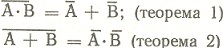
Для проверки теоремы 1 воспользуемся следующими двумя запросами:
all (х у : tab (2 Nand x у))
all (х: (1 1 Not Not Or) com x)
Сравнив приведенные ниже ответы Пролог-системы, убедимся в том, что анализируемые функции из левой и правой частей формулировки теоремы 1 идентичны:
(0 0) 1 (0 0 1)
(0 1) 1 (0 1 1)
(1 0) 1 (1 0 1)
(1 1) 0 (1 1 0)
Аналогичным способом можно доказать правильность теоремы 2. Рассмотренная программа может быть усовершенствована с помощью дополнительного отношения, которое позволяет проверять эквивалентность двух логических выражений. Это отношение называется equiv и имеет следующий вид:
(X Y | Z) equiv (X Y | x) if
(forall ((X Y | x) com у then (X У | Z) com y)
Эта запись означает, что две логические схемы эквивалентны, если они формируют одинаковые выходные сигналы для каждой комбинации входных сигналов. В том случае, когда требуется проверить эквивалентность некоторой сложной схемы и элементарной, состоящей из одного элемента, удобно пользоваться фиктивным элементом - проводником Link, непосредственно соединяющим вход первого уровня со входом второго. Для этого дополним отношение
(Link 0) fn 0
(Link 1) fn 1
Программа Link соответствует элементу, повторяющему на выходе свой же входной сигнал. Теперь можно воспользоваться отношением equiv, например, следующим образом:
is ((1 1 Link Link Nand) equiv (1 1 Not Not Or)
YES
&.
Утвердительный ответ подтверждает правильность формулировки теоремы 1. Очевидно, что такой способ доказательства эквивалентности логических схем удобнее, чем рассмотренный раньше, при котором приходилось вручную сравнивать таблицы истинности. На рис. 4.3 показаны логические схемы, иллюстрирующие теоремы 1 и 2.
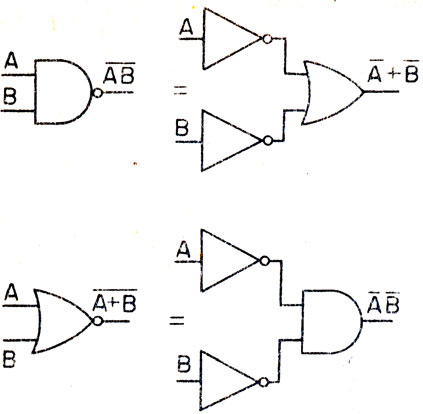
Рис. 4.3. Иллюстрации к теоремам 1 и 2
Упражнение 4.10
а. Проверьте теорему 2 с помощью отношения equiv.
б. С помощью отношения tab или com получить таблицы истинности левой и правой частей теоремы 2 и убедиться, что они совпадают.
Мы использовали программу 4.10 для того, чтобы подтвердить или отвергнуть какую-либо гипотезу о равенстве одних логических схем другим. Следующим шагом будет получение отношения, которое способно генерировать новые логические схемы, эквивалентные исходным. Такое отношение (isequiv), представленное в программе 4.11, включает в себя все отношения, использованные ранее при анализе логических схем. В рассматриваемой программе отношение igate предназначено для получения логических схем, построенных на элементах с инвертированным выходом Nor, Nand и Not, которые были бы эквивалентны исходным схемам, содержащим только элементы без инвертирования Ог, And и Link. Если нужно получить все эквивалентные схемы, то отношение igate следует переписать, дополнив соответствующий список так, чтобы он содержал все элементы, включая Link.
(Link ∅) fn ∅
(Linkl)fn 1
(Not ∅) fn 1
(Not 1) fn ∅
(And ∅|X) fn ∅
(And 1 1) fn 1
(And 1|X) fn Y if
(And |X) fn Y
(Or ∅∅) fn ∅
(Or ∅|X) fn Y if
(Or |X) fn Y
(Or 1|X) fn 1
(Nand |X) fn Y if
(And |X) fn Z and
(Not Z)fn Y
(Nor X)fn Y if
(Or X)fn Z and
(Not Z)fn Y
(X) b 1 if
X ON (0 1)
X b Y if
1 LESS Y and
SUM(1 Z Y)and
x b 1 and
у b Z and
APPEND (x у X)
tab(X Y Z x)if
Z b X and
(Y Z)fn x
(X Y Z x y) com z if
tab (XZ X1 Y1) and
tab(Y x Z1 x1)and
APPEND(X1 Z1 y1) and
(y Y1 x1) fn z1 and
APPEND (y1(z1)z)
(X Y Z x y) isequiv (X Y z XI Yl) if
igate Z and
igate x and
igate у and
(X Y Z x y) equiv (X Y z X1 Y1)
(XY|Z) equiv (XY|x) if
(forall (X Y| x) com у then (X Y|Z) com y)
igate X if
X ON (Not Nor Nand)
Приведем пример иепользования программы 4.11:
all (x : х isequiv (2 2 And And And)
(2 2 Nand Nand Nor)
No (more) answers
&.
Результат, полученный Пролог-системой после анализа соответствующих таблиц истинности, подтверждает истинность еле дующего равенства:
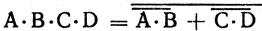
Доказательство теорем, а также генерация формулировок новых теорем входят в ряд наиболее распространенных задач математической логики и искусственного интеллекта. Каждому изучающему программирование на Прологе будет полезно написать программу, аналогичную рассмотренной в данном разделе, но для такой предметной области, которая больше соответствует его профессиональным интересам. Для читателей, специализирующихся в области электроники, можно порекомендовать в качестве такого упражнения усовершенствовать программу 4.11, дополнив ее отношениями, позволяющими описывать элементы последовательного действия, такие, как триггеры, счетчики и регистры сдвига. Полученная в результате программа должна строить логическую схему по описанию ее работы, представленному в виде спецификаций.
Упражнение 4.11
С помощью программы 4.11 проверить следующие равенства:
|
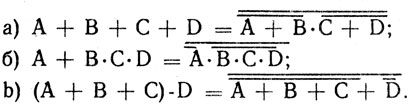
ПОИСК:
|
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'