Задачи и дополнения
1. Весом вектора u (обозначается ω(u)) называют число его ненулевых координат. Понятно, что расстояние Хемминга между двумя векторами u1 и u2 равно весу их разности ω(u1 - u2). Это позволяет упростить отыскание кодового расстояния линейного кода. Именно, справедливо следующее утверждение:
Кодовое расстояние линейного кода равно минимальному весу его ненулевых кодовых слов:
d(V) = min ω(υ). υ∈V υ≠0
Предоставляем читателю доказать это утверждение.
2. Пусть двоичный линейный код V содержит хотя бы одно слово нечетного веса. Доказать, что число всех таких слов составляет тогда ровно половину от общего числа кодовых слов.
Указание. Убедиться, что множество всех кодовых слов четного веса есть подпространство и найти смежные классы кода V по этому подпространству.
3. Рассмотрим матрицу порядка qk × n, в качестве строк которой взяты все кодовые векторы личного линейного (n, k)-кода. Будем предполагать, что ни один столбец этой матрицы не является нулевым (иначе, вычеркнув нулевой столбец, мы получили бы код с тем же кодовым расстоянием, но меньшей длины). Показать, что в каждом столбце этой матрицы каждый из элементов поля встречается ровно qk-1 раз. Пользуясь этим, убедиться, что суммарный вес всех кодовых слов равен n(q-1)qk-1.
Указание. Проверить, что множество всех кодовых слов, содержащих 0 в некоторой фиксированной позиции, есть подпространство, и найти разложение кода в смежные классы по этому подпространству.
4. Предположим, что кодовый вектор υ = (x1, х2, ..., хn) имеет вес, равный ω, xk1, хk2, ..., хkω - его ненулевые координаты. Из проверочных соотношений (1) получаем тогда:
b1k1xk1 + b1k2xk2 + ... + b1kωxkω = 0,
. . . . . . . . . . . . . . . . . . . . . .
bmk1xk1 + bmk2xk2 + ... + bmkωxkω = 0.
Это означает, что столбцы проверочной матрицы с номерами k1, k2, ..., kω линейно зависимы. Следовательно, каждому кодовому вектору веса до соответствует до линейно зависимых столбцов проверочной матрицы. Верно и обратное утверждение.
Отсюда вытекает, что кодовое расстояние линейного кода равно d тогда и только тогда, когда в проверочной матрице найдется d линейно зависимых столбцов, а всякая система из меньшего числа столбцов линейно независима.
5. Доказать, что двоичный линейный код исправляет любые одиночные ошибки тогда и только тогда, когда все столбцы его проверочной матрицы ненулевые и различные. Верно ли это для любого линейного кода?
6. Как изменится кодовое расстояние двоичного линейного кода при добавлении ко всем его словам одного проверочного символа, задающего общую проверку на четность?
7. Двоичный (8,4)-код задан порождающей матрицей

Найти его проверочную матрицу и кодовое расстояние.
То же задание для троичного (6,3)-кода с порождающей матрицей

8. Два кода V1 и V2 называются эквивалентными, если кодовые слова одного кода получаются из кодовых слов другого некоторой перестановкой символов (одной и той же для всех кодовых слов). Поскольку при этом веса кодовых слов остаются без изменений, то кодовые расстояния двух эквивалентных кодов совпадают, поэтому одинаковы также их возможности исправлять или обнаруживать ошибки. Ясно, что если порождающие матрицы кодов получаются одна из другой путем перестановки столбцов, то коды эквивалентны.
Эквивалентными являются, например, коды V1 и V2 со следующими порождающими матрицами:


Однако связь между матрицами эквивалентных кодов может быть и более сложной. Причина заключается в том, что порождающая матрица данного кода определена неоднозначно.
9. В предыдущем примере код V1 эквивалентен систематическому коду V2. Это не исключение, а правило, поскольку справедливо следующее утверждение:
Всякий линейный код эквивалентен систематическому коду.
Доказательство, которое рекомендуется продумать читателю, основывается, в сущности, на известном современному школьнику методе Гаусса исключения неизвестных.
Последовательность действий, приводящих произвольный код к систематическому, продемонстрируем на примере матрицы (11) (задача 7).
Вычитая из четвертой строки матрицы (11) первую, получим:

далее, вычитая из первой строки вторую, приходим к матрице

Получающиеся при этих преобразованиях матрицы также порождают исходный код. Осуществим теперь перестановку столбцов, чтобы слева лучить единичную матрицу - пятый столбец поставим на место второго восьмой - на место третьего, седьмой - на место четвертого столбца В итоге получим порождающую матрицу систематического кода

10. Показать, используя соотношения (7), что для систематического кода с порождающей матрицей (9) в качестве проверочной можно взять следующую матрицу:

11. Пусть V - произвольный линейный (n, k)-код. Рассмотрим множество V' всех векторов пространства Ln, ортогональных каждому из кодовых векторов υ ∈ V. Нетрудно проверить, что V' является под пространством в Ln и, следовательно, может рассматриваться как линейный код. Код V называется дуальным к исходному коду V.
Убедиться, что если G и Н - порождающая и проверочная матрицы кода V, то они служат соответственно проверочной и порождающей матрицей дуального кода V'.
Простейший пример кодов, дуальных друг к другу, - это код с повторением и код с общей проверкой на четность.
12. Одним из способов получения кодов, обладающих большим кодовым расстоянием, а значит, и высокой корректирующей способностью, является комбинирование двух или нескольких кодов. Примером такого комбинирования является рассматриваемая здесь конструкция. Она дает код, который является обобщением матричного кода из § 8 с проверками на четность по строкам и столбцам.
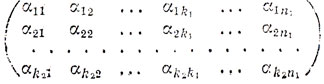
Пусть дано слово, содержащее k = k1k2 информационных символов. Разобьем множество этих символов на k2 блоков по k1 символов в каждом и запишем результат в виде квадратной матрицы порядка k2 × k1:

В первой строке этой матрицы выписаны по порядку символы первого блока, во второй - символы второго и т. д.
Рассмотрим теперь произвольный систематический линейный код V1 длины n1 с k1 информационными символами и с тем же самым кодовым алфавитом. Строки матрицы (12) закодируем указанным кодом. Для этого к каждой строке припишем n1-k1 проверочных символов таким образом, чтобы выполнялись проверочные соотношения кода V1.
Далее каждый столбец получившейся матрицы порядка k2 × n1,
закодируем точно таким же способом с помощью линейного (n2, k2) кода V2.
В результате получим матрицу порядка n2 × n1:
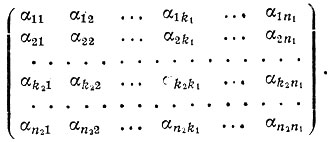
Выписывая элементы этой матрицы "по строкам", мы и составим кодовое слово, отвечающее исходному слову. Оно, очевидно, однозначно определяется матрицей (12).
Построенный код называется произведением кодов V1 и V2 и обозначается V1 ⊗ V2.
Пусть теперь k, k1, k2 - числа информационных символов кодов V1 ⊗ V2, V1 ⊗ V2, а n, n1, n2 - длины этих кодов. Из построения кода V1 ⊗ V2 сразу же вытекает, что
k = k1k2 и n = n1n2.
Менее очевидно аналогичное соотношение между кодовыми расстояниями d, d1, d2 тех же кодов: d = d1 · d2. Доказательство этого факта предоставляем читателю.
Предлагаем читателю также выяснить, какова связь между количеством ошибок, исправляемых кодами V1, V2 и V1 ⊗ V2.
Проиллюстрируем сказанное примером. Пусть k = 8, k1 = 4, k2 = 2. В качестве кода V1 возьмем (7,4)-код Хемминга, записав предварительно его порождающую матрицу в систематической форме:

в качестве V2 - (3,2)-код с общей проверкой на четность. Составим кодовое слово кода V1 ⊗ V2, соответствующее исходному слову 00101110 с восемью информационными символами. Запишем его в виде матрицы порядка 2 × 4:
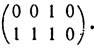
В результате кодирования строк (7,4)-кодом Хемминга (см. правило (6)) получим матрицу порядка 2 × 7:

Кодирование столбцов этой матрицы сводится к добавлению в каждом столбце символа общей проверки на четность. Получившейся в итоге матрице порядка 3 × 7

соответствует следующее кодовое слово кода V1 ⊗ V2:
001001111100001100011.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'