11. Линейные или групповые коды

Большинство рассмотренных выше кодов обладало следующим свойством: сумма (и разность) двух кодовых слов также являлась кодовым словом. Для кода с повторением это свойство очевидно. Ясно оно и для кода с общей проверкой на четность, потому что сумма двух слов с четным числом единиц есть также слово с четным числом единиц.

В § 9 был рассмотрен код Хемминга с системой проверочных соотношений (5). Обобщим теперь этот пример, выбрав в качестве кодового алфавита некоторое конечное поле F. Каждое слово x₁x₂ ... x_n этого алфавита будем отождествлять с вектором (x₁, x₂, ..., x_n) n-мерного пространства L_n (в котором координаты векторов являются элементами F). Вектор, соответствующий кодовому слову, будем называть кодовым. Систему проверочных соотношений запишем в виде системы уравнений:

с коэффициентами b_ij из F. Код, состоящий из всех слов х₁х₂ ... x_n, для которых справедливы соотношения (1), называют кодом с проверками на четность.

Для такого кода выполняется следующее свойство: если векторы (a₁, а₂, ..., а_n) и (b₁, b₂, ..., b_n) являются кодовыми, а значит, решениями системы (1), то и их сумма (а₁ + b₁, а₂ + b₂, ..., а_n + b_n) также является решением этой системы и потому кодовым вектором. Справедливо и другое свойство решений системы (1): если, α - элемент поля F и (a₁, а₂, ..., а_n) - решение системы (1), то и вектор (αa₁, αа₂, ..., αа_n) также является решением системы (1). Оба отмеченных свойства проверяются непосредственной подстановкой в систему (1) векторов

Вместе эти свойства означают, что код с проверками на четность образует линейное подпространство в пространстве L_n всех n-буквениых слов. По этой причине коды с проверками на четность называют линейными кодами (двоичные линейные коды называют также групповыми). Если кодовое подпространство в пространстве L_n имеет размерность k, то употребляют для большей определенности термин линейный (n, k)-код.

Имеется очень много причин, по которым линейные коды являются важнейшими в теории кодирования. Одна из них связана с удобствами в обнаружении и исправлении ошибок, как это видно из примера, рассмотренного в § 9. Другая причина - это возможность компактного задания кода. Действительно, в случае линейного кода нет необходимости указывать полный список кодовых слов, ведь код вполне определен системой линейных уравнений (1) или матрицей этой системы (проверочной матрицей):

В дальнейшем мы будем предполагать, что строки этой матрицы линейно независимы.

К числу других достоинств линейных кодов, которые связаны с предыдущими, относятся простые алгоритмы кодирования и декодирования, легко реализуемые электронными переключательными схемами. Вообще, можно сказать, что бурное развитие теории кодирования, которое происходило в последние десятилетия, объясняется главным образом тем, что к линейным кодам приложим хорошо развитый аппарат линейной алгебры и теории конечных полей.

Возвращаясь к рассмотренным ранее кодам, легко найдем их проверочные матрицы. Так, для кода с общей проверкой на четность имеем одно проверочное соотношение x₁ + x₂ + ... + x_n = 0; соответственно этому проверочная матрица состоит из одной строки и имеет вид

Из проверочных соотношений для кода с повторением

получаем следующую проверочную матрицу:

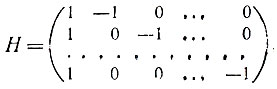
Наконец, проверочная матрица двоичного кода Хемминга длины 7, как это следует из соотношений (5) § 9, выглядит так:

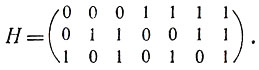
Имеется и другой способ матричного задания линейного кода. Он основан на том, что во всяком подпространстве линейного пространства можно выбрать базис, т. е. такую линейно независимую систему векторов, через которые линейно выражаются все вообще векторы подпространства. Пусть

- базисные векторы линейного кода. Тогда всевозможные кодовые векторы исчерпываются линейными комбинациями

где коэффициенты α_i - любые элементы исходного поля. Таким образом, система базисных векторов (3) полностью определяет линейный (n, k)-код. Матрица G, составленная из них,

называется порождающей матрицей кода.

Заметим, что базис можно выбрать не единственным образом, поэтому порождающая матрица G определена неоднозначно. Последнее, впрочем, верно и в отношении проверочной матрицы H.

Легко указать порождающую матрицу кода с повторением; она имеет вид:

В качестве базисных векторов двоичного кода с общей проверкой на четность могут быть взяты, например, следующие n-1 векторов:

Поэтому матрица

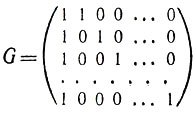
является порождающей матрицей этого кода.

При использовании линейного кода для передачи сообщений полезно знать и порождающую, и проверочную матрицу. С помощью порождающей матрицы удобно кодировать сообщения. Поскольку линейный (n, k)-код с порождающей матрицей (5) имеет q^k кодовых слов (любой из k коэффициентов в (4) можно выбрать q способами), он позволяет закодировать все сообщения длины k в алфавите из q символов. Если А = α₁α₂ ..., α_k - такое сообщение (α_i - информационные символы), то самое удобное - сопоставить ему кодовый вектор я, совпадающий с линейной комбинацией (4) строк порождающей матрицы. Вектор а нетрудно записать в матричном виде, используя правило умножения матриц:

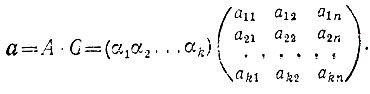
Пример. Пусть дана порождающая матрица двоичного линейного кода:

Этот код содержит 2⁴ = 16 кодовых слов, которыми можно закодировать все двоичные сообщения длины 4. Если, например, А = (0101), то для соответствующего кодового вектора имеем:

О роли проверочной матрицы мы скажем в дальнейшем - она используется в основном при декодировании полученных сообщений и для исправления ошибок.

Выясним, как связаны порождающая и проверочная матрицы, и как по одной из них найти другую. Обратимся к соотношениям (1). Всякая строка порождающей матрицы, являясь кодовым вектором, удовлетворяет каждому из соотношений (1), т. е. для любых i и j

Другими словами, любая строка порождающей и любая строка проверочной матриц ортогональны друг другу. Матричная запись равенств (7) выглядит так:

(0 означает здесь нулевую матрицу).

Заметим также, что из соотношений (1) вытекает равенство

справедливое для каждого кодового вектора υ.

Для отыскания порождающей матрицы нужно фактически найти k = n - m линейно независимых решений системы (1). Эти решения как раз и будут строками порождающей матрицы.

Пример. Найдем порождающую матрицу кода Хемминга длины 7 с проверочной матрицей (2). В данном случае требуется найти 4 независимых решения следующей системы:

Разрешаем систему относительно неизвестных x₁, х₂, x₄:

Неизвестным x₃, х₅, x₆, х₇ можно придавать любые значения; тогда из равенств (8) могут быть определены оставшиеся неизвестные х₁, x₂, х₄. Придавая поочередно одному из неизвестных x₃, х₅, x₆, х₇ значение 1, а остальным - 0, получим 4 решения:

которые, как читатель может убедиться, линейно независимы. Составленная из этих решений матрица

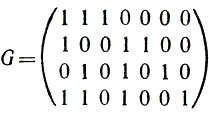
и является искомой порождающей матрицей.

По поводу сказанного в этом параграфе возникает множество вопросов. Например, как, зная порождающую и проверочную матрицы, выяснить корректирующие способности данного кода; как реализовать эти способности (т. е. каким должен быть алгоритм декодирования, исправляющий или обнаруживающий ошибки); как, наконец, после исправления ошибок выделить информационные символы?

Остановимся вначале на последнем вопросе. Пусть, исправив ошибки, мы получили некоторый кодовый вектор а = (а₁, а₂, ..., а_n). Тогда соответствующие ему информационные символы α₁, α₂, ..., α_k определяются из равенства (6). Иными словами, вектор (α₁, α₂, ..., α_k) есть решение (как можно показать, - единственное) системы линейных уравнений:

Хотя задача отыскания этого решения и не содержит принципиальных трудностей, она может потребовать громоздких вычислений. Однако выделение информационных символов предельно упрощается, если использовать для кодирования так называемые систематические линейные коды.

Линейный (n, k)-код называется систематическим, если его порождающая матрица имеет вид

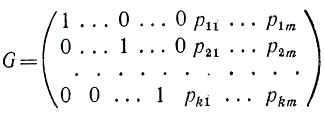
или вид

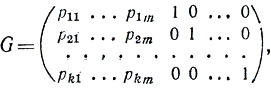
т. е. если она получается приписыванием к единичной матрице порядка k некоторой матрицы из k строк и m = n - k столбцов (иначе говоря, матрицы порядка k × m).

В случае (9) равенство (6) принимает вид:

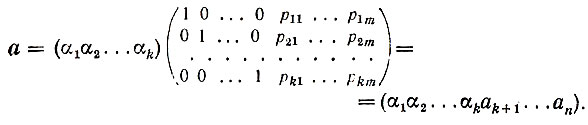
Таким образом, первые k символов любого кодового слова как раз и оказываются информационными, а остальные (они являются проверочными) связаны с информационными символами соотношениями:

Равенства (10), очевидно, образуют систему проверочных соотношений систематического линейного кода. Очень важно, что всякий линейный код в некотором смысле эквивалентен систематическому (см. дополнение 9).

Дальнейшее прольет свет и на другие вопросы, поставленные выше.