Задачи и дополнения
1. Убедиться, что не существует кода длины 20, содержащего 1000 кодовых слов и исправляющего любые комбинации из трех и менее ошибок.
2. Использовать верхнюю оценку Хемминга для доказательства следующего утверждения:
Для всякого q-ичного линейного (n, k)-кодa с кодовым расстоянием d = 2t + 1 величина logqVt служит нижней границей для числа m проверочных символов:
m ≥ logqVt.
3. Для оценки "качества" линейного кода можно пользоваться так называемой границей Варшамова - Гильберта. Применительно к двоичным кодам указанная оценка основывается на следующем утверждении:
Если выполняется неравенство
1 + С1n-1 + С2n-1 + ... + Cd-2n-1 < 2m, (4)
то существует линейный (n, k)-код с кодовым расстоянием, не меньшим d, имеющий не более m проверочных символов.
Для доказательства доетаточно построить матрицу Н порядка m × n, в которой любые d-1 столбцов линейно независимы; она и будет служить проверочной матрицей искомого кода (см. § 11, дополнение 4). В качестве первого столбца Н можно взять любой ненулевой вектор длины m. Пусть уже выбрано i < n столбцов, любые d-1 из которых линейно независимы. Всевозможных линейных комбинаций этих i столбцов, содержащих ровно j слагаемых, имеется не более Сji, и, следовательно, число всех линейных комбинаций, содержащих d-2 или меньше столбцов, не превосходит числа
C1i + C2i + ... + Cd-2i.
Но в силу (4) это число меньше величины 2m-1, т. е. общего количества ненулевых столбцов. Поэтому мы можем добавить по крайней мере еще один столбец, не равный ни одной из указанных линейных комбинаций. В получившейся при этом системе из i + 1 векторов любые d-1 векторов по-прежнему будут линейно независимы. Продолжая эту процедуру присоединения столбцов, мы и построим искомую матрицу Н.
4. Утверждение, доказанное в дополнении 3, обобщается на случай линейного кода над произвольным полем из q элементов; неравенство (4) заменяется при этом на следующее неравенство:
∑d-2i=0 Cin-1 (q - 1)i < qm.
5. Можно указать еще одну простую оценку для кодового расстояния. Поскольку суммарный вес ненулевых кодовых слов q-ичного линейного (n, k)-кода есть nqk-1(q - 1) (см. § 11, дополнение 3), то средний вес ненулевых кодовых слов равен nqk-1(q - 1) / (qk - 1). Ясно, что он не может быть меньше минимального веса, совпадающего с кодовым расстоянием d. Таким образом,
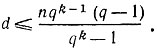
Мы получили границу, называемую верхней границей Плоткина.
Оценка (5) обобщается на случай произвольного личного кода длины и, содержащего М кодовых слов. В этом случае
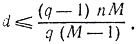
6. Из оценки Хемминга (1) также можно получить границу для кодового расстояния. Пусть код длины n, исправляющий t и меньшее число ошибок, содержит М кодовых слов. В силу определения
М (n, 2t + 1) и оценки (1) М ≤ М (n, 2t + 1) ≤ qn/Vt. Отсюда получаем:
1 + C1n + ... + Ctn ≤ qn / M. (7)
Неравенство (7) дает верхнюю границу для t, а значит, и для кодового расстояния d = 2t + 1.
Граница Хемминга точнее границы Плоткина для кодов, избыточность которых не слишком велика (отношение числа проверочных символов к общему числу символов не превосходит 0,6). В остальных случаях точнее граница Плоткина.
Например, для двоичного (16,5)-кода оценка (5) дает d ≤ 8, а из оценки (7) получается t ≤ 4, т. е. d ≤ 9.
7. Имеются и нелинейные совершенные коды, но их также немного. Во всяком случае известно, что любой нетривиальный совершенный код над любым полем должен иметь те же самые параметры (длину, кодовое расстояние и число кодовых слов), что и один из кодов Хемминга или Голея. Все же полное описание нелинейных совершенных кодов, исправляющих одиночные ошибки, пока не получено (см. по этому поводу [12], задача 6.6).
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'