16. Кодирует и декодирует ЭВМ

Заголовок этого параграфа не следует понимать буквально. Вряд ли было бы целесообразно привлекать универсальные ЭВМ для кодирования и декодирования с помощью линейных и циклических кодов. Однако устройства или схемы, предназначенные для этих целей, состоят из тех же элементов, что и любая ЭВМ, так что такие схемы, если угодно, можно рассматривать как специализированные мини-ЭВМ. В случае двоичных кодов применяются элементы двух основных типов:

16. Кодирует и декодирует ЭВМ

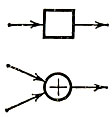
Ячейка памяти (или триггер), которая может находиться в двух состояниях: одно из них соответствует символу 0, другое - символу 1. Ячейка памяти имеет один вход и один выход.

Двоичный сумматор, осуществляющий сложение по модулю 2. Сумматор имеет два входа и один выход.

Устройства, составленные из этих элементов, позволяют легко перемножать и делить двоичные многочлены, а это как раз те операции, которые приходится выполнять при использовании циклических кодов.

В качестве первого примера рассмотрим схему, осуществляющую умножение произвольного двоичного многочлена /(X) на многочлен 1 + X² + X³. Эта схема представлена на рис. 14 и состоит всего из трех ячеек памяти и двух сумматоров. Поясним принцип ее работы.

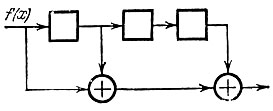
Рис. 14

Первоначально все ячейки памяти содержат нули, а на од поступают коэффициенты многочлена f(X) = a_nXⁿ + а_n-1Х^n-1 + ... + а₀, начиная с коэффициентов при старших степенях. Коэффициент а_n без изменений передается на выход и запоминается в первой ячейке памяти (рис. 15, а).

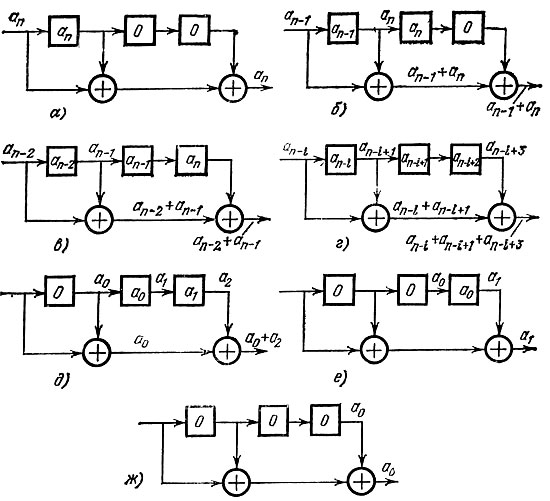
Рис. 15

В следующем такте работы (рис. 15, б) в первую ячейку памяти попадет коэффициент а_n-1, а коэффициент а_n сдвигается в следующую ячейку памяти. При этом на входах первого сумматора окажутся значения а_n и а_n-1, а на выходе - их сумма по модулю 2.

В третьем такте (рис. 15, в) произойдет дальнейший сдвиг коэффициентов в ячейках памяти, а на выходе первого сумматора и всей схемы появится сумма а_n-2 + а_n-1.

На рис. 15, г показано состояние схемы на i-м такте, когда на вход подан коэффициент а_n-i(i ≤ n).

Последние три такта отражены на рис. 15, д-ж.

Итак, на выходе схемы появится следующая последовательность из n + 3 коэффициентов:

Эта последовательность соответствует многочлену

Непосредственно проверяется, что этот многочлен как раз и есть нужное нам произведение

Аналогично устроена схема умножения на произвольный многочлен

над любым полем (рис. 16). В этой схеме ячейки памяти хранят элементы поля F, так что число различных состояний ячеек должно совпадать с числом элементов в F. Ячейки памяти, как это видно из предыдущего описания, не только "запоминают", но и "сдвигают" поступающие в них коэффициенты (играют роль сдвигающего регистра). Сумматоры осуществляют сложение по правилам сложения в поле F. Кроме того, в схему введены добавочные устройства, производящие умножение на элемент g_i ∈ F (на рис. 16 эти устройства показаны кружками, помеченными соответствующими множителями). В двоичном случае особых устройств для этого не требуется: если g_i = 1, то в соответствующем месте схемы имеется "вертикальное" соединение и двоичный сумматор, в противном случае они отсутствуют.

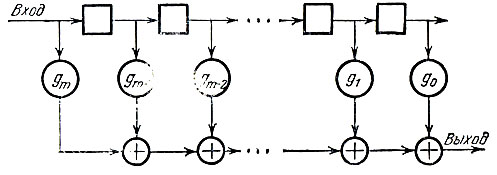
Рис. 16

Столь же просты схемы деления многочлена на многочлен с остатком. Вот, например, как устроена схема деления на многочлен 1 + Х² + Х³ (рис. 17).

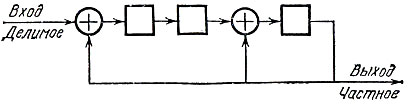
Рис. 17

На вход поступают коэффициенты делимого, начиная со старших степеней, на выходе последовательно появляются коэффициенты частного. После окончания деления в ячейках памяти слева направо оказываются записанными коэффициенты остатка, начиная с младших степеней. Проследим последовательность работы схемы при делении на Х³ + Х² + 1 многочлена X⁵ + X⁴ + X³ + X + 1. Деление углом дает:

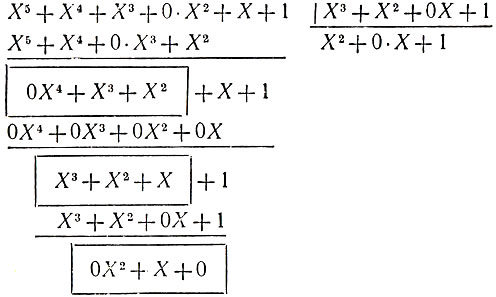
(рамочками выделены последовательные частичные остатки).

В первые три такта работы схемы старшие коэффициенты делимого сдвигаются по ячейкам памяти. При этом старший коэффициент (при X⁵) окажется в крайней правой ячейке (рис. 18, а). Все это время на "нижних" входах сумматоров сохраняются нулевые элементы, не влияющие на работу схемы. В следующем такте (рис. 18, б) старший коэффициент сдвигается на выход схемы, одновременно попадая на нижние входы сумматоров. На вход схемы поступает нулевой коэффициент при X². В первую ячейку записывается выход первого сумматора, равный 1 + 0 = 1, во вторую - содержимое первой ячейки в предыдущем такте (т. е. 1), а в третью - выход второго сумматора, равный 1 + 1 = 0. В итоге в ячейках памяти сдвигающего регистра оказываются записанными коэффициенты первого из обведенных рамочкой остатков.

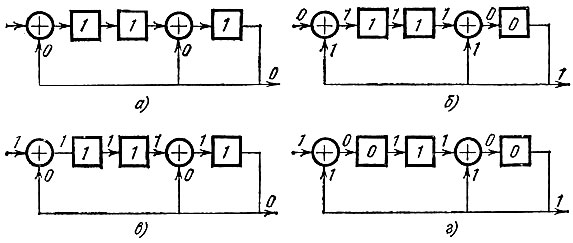
Рис. 18

На рис. 18, в показано состояние схемы после еще одного такта ее работы. Теперь уже содержимое ячеек - коэффициенты второго из заключенных в рамочку остатков.

Еще один такт работы схемы переводит ее в конечное состояние (рис. 18, г). В ячейках памяти получены коэффициенты остатка, а последовательность символов 1, 0, 1 на выходе - это коэффициенты частного.

Приведем без комментариев схему, осуществляющую деление с остатком на произвольный многочлен g(X) (рис. 19), предоставляя читателю самому разобраться в принципе ее действия.

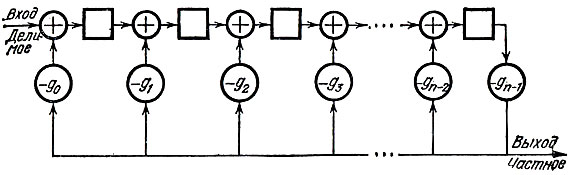
Рис. 19

Схемы умножения и деления многочленов, рассмотренные нами, - это, по существу, уже готовые кодирующие устройства (или, как их называют, кодеры) для циклических кодов. В самом деле, вспомним правило кодирования линейным (n, k)-кодом. Если А = α₀ ... α_k-1 - произвольное сообщение длины k, то ему сопоставляется кодовый вектор

где G - порождающая матрица линейного кода.

Разумеется, правило остается в силе и для любого циклического кода, но на языке многочленов ему можно придать теперь иную, гораздо более удобную форму.

Если а(х) - многочлен, соответствующий вектору а, и

- многочлен, соответствующий сообщению A, то равенство (1) перейдет в равенство многочленов

где g(x) - порождающий многочлен циклического кода.

Для того чтобы убедиться в этом, достаточно подставить (1) матрицу G из формулы (9) § 11 и проверить, что координаты получающегося вектора служат коэффициентами многочлена A(x)g(x).

Итак, операция кодирования сводится к умножению многочленов. При этом можно считать, что речь идет об обычном умножении многочленов, поскольку степень g(x) равна m, а степень А(х) меньше n-m, так что сумма степеней этих многочленов меньше n. Но схемы, которые мы здесь рассмотрели (рис. 14 и 16), как раз и вычисляют обычное произведение многочленов. Первая из них может служить кодером для циклического (7,4)-кода с порождающим многочленом x³ + x² + 1, а вторая - для произвольного циклического кода с порождающим многочленом g(x). Если на вход последней поступают информационные символы α₀, α₁, ... α_n-1 (коэффициенты многочлена А(х)), то на выходе согласно (2) будем иметь коэффициенты кодового многочлена а(х).

На основе схем деления чрезвычайно удобно строить кодеры для систематических циклических кодов, в которых информационные символы отделены от проверочных (см. дополнение 4 к этому параграфу).

Даже наше беглое знакомство с устройствами кодирования показывает, что все они имеют унифицированную структуру. Как видно из рис. 16, путем определенных видоизменений схемы, предназначенной для одного кода, можно получить схему кодирования для другого кода. Поэтому в ряде случаев целесообразно использовать не конкретные схемы для каждого кода, а достаточно разветвленное устройство с большим набором стандартных элементов, работу которого можно было бы перестраивать, вводя в него ту или иную программу. Такое устройство, в сущности, и есть специализированная мини-ЭВМ с программным управлением.

В задачу декодирования входит исправление и обнаружение ошибок, и эта процедура много более сложная, чем кодирование. Но устройства, подобные рассмотренным "мини-ЭВМ", позволяют решить и эту задачу. В отличие от кодеров, которые выглядят более или менее стандартно для всех циклических кодов, декодирующие устройства (или декодеры) отличаются большим разнообразием, и то как они устроены, зависит и от типа кода, и в особенности, от способа декодирования.

Кроме синдромного декодирования, о котором мы рассказывали в § 12, существуют еще ряд других методов, так или иначе связанных с вычислением синдрома. Для любого из них принципиальная схема декодера выглядит так, как показано на рис. 20.

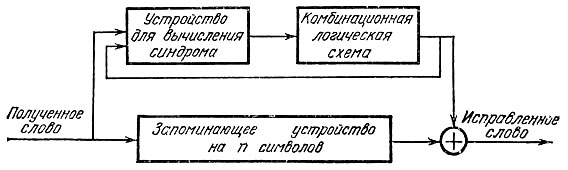
Рис. 20

Наиболее сложной частью такого декодера является комбинационная логическая схема, которая по вычисленному синдрому находит положение ошибочных символов. Устройство этой логической схемы целиком определяется алгоритмом декодирования, а многообразием логических схем в свою очередь определяется большое разнообразие декодеров. Сложность практической реализации декодера всецело зависит от характера логической схемы. Комбинационная схема исключительно проста, как мы увидим, в случае декодеров, только обнаруживающих ошибки или исправляющих лишь одиночные ошибки, но существенно сложнее для декодеров, исправляющих кратные ошибки. В следующих двух параграфах мы познакомимся с методами так называемого мажоритарного декодирования, которые позволяют значительно упростить комбинационную логическую схему.

Что же касается устройств для вычисления синдрома, то здесь особой проблемы нет: они реализуются по тому же принципу, что и кодеры циклических кодов. Для этой цели, оказывается, могут быть использованы схемы деления многочленов.

Чтобы убедиться в этом, рассмотрим матрицу H, по столбцам которой стоят коэффициенты остатков r_i(х) от деления многочленов xⁱ(i = 0, 1, ..., n-1) на порождающий многочлен g(x). Запишем ее условно в виде:

Можно показать, что матрица Н является проверочной для рассматриваемого кода (см. дополнение 2 к этому параграфу).

Если u = (u₀, u₁, ..., u_n-1) - принятый вектор, то его синдром uН^T будет равен

Выражение (3) совпадает с остатком от деления многочлена

на порождающий многочлен g(x). Таким образом, любая хема деления, вычисляющая остаток, - например, схема, представленная на рис. 19, - может быть использована как уставная часть декодера для получения синдрома.

На рис. 21 приведена схема декодера, предназначенного только для обнаружения ошибок.

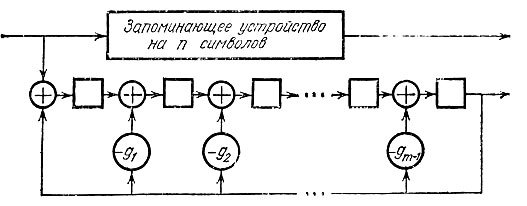
Рис. 21

Полученное слово одновременно вводится в запоминающее устройство и в схему деления. К моменту заполнения запоминающего устройства в ячейках схемы деления будет получен остаток от деления на g(x), который равен синдрому. Если синдром равен нулю, то слово передается адресату, в противном случае прием прекращается и передающей стороне посылается запрос на повторную передачу.

Не намного сложнее схема декодера для кодов Лемминга, исправляющих одиночные ошибки. В качестве примера рассмотрим декодер для (7,4)-кода с порождающим многочленом 1 + х² + х³. Его схема представлена на рис. 22. Она включает в себя наряду со схемой деления и запоминающим устройством также и логическую схему. Последняя устроена так, что на ее выходе появляется 1, только если на вход из ячеек памяти подается комбинация 011, равная последнему столбцу проверочной матрицы

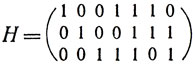
(которая построена указанным выше способом из остатков от деления многочленов хⁱ на порождающий многочлен 1 + х² + х³).

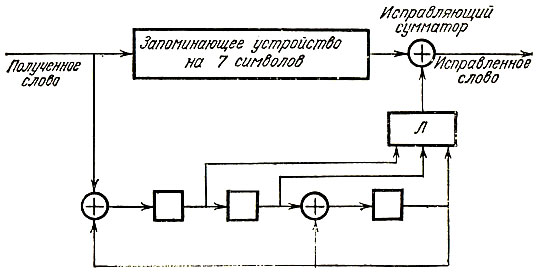
Рис. 22

Предположим теперь для примера, что ошибка в слове u₀ u₁ u₂ u₃ u₄ u₅ u₆ произошла в символе u₃ - четвертом по порядку. Как мы знаем, синдром в этом случае будет совпадать с четвертым столбцом матрицы H, т. е. будет равен вектору (1 0 1). Следовательно, после семи тактов работы в запоминающем устройстве окажется слово u₀ u₁ u₂ u₃ u₄ u₅ u₆, а в трех последовательных ячейках схемы деления - комбинация 1 0 1, На восьмом такте из запоминающего устройства на исправляющий сумматор поступит символ u₆, на вход логической схемы сдвинется комбинация 1 0 1, на ее выходе окажется 0, и символ u₆ без изменений поступит на выход всей схемы. При этом, как нетрудно проверить, в ячейках схемы деления окажется комбинация 1 1 1 (на вход всей схемы, начиная с восьмого такта поступают нули). В следующих трех тактах из запоминающего устройства будут последовательно поступать символы u₅, u₄, u₃, а вход логической схемы - комбинации 111, 110, 011, а на ее выходе получатся поочередно 0, 0 и 1. Поэтому символы u₅ и u₄ поступят на выход неисправленными, а ошибочный символ u₃ исправится. Проследив дальнейшие три такта, можно убедиться, что символы u₂, u₁ и u₀ исправляться не будут. В результате на выходе схемы окажется слово, в котором будет исправлен только ошибочный символ u₃.

Совершенно аналогично происходит исправление ошибки в любой другой позиции.