1. Сравнения и классы вычетов
Исходным материалом для нас остаются пока все же числа. Два целых числа а и b называют сравнимыми по модулю n (n - натуральное), если их разность а - b делится на n без остатка *). Это выражают следующей записью:
а ≡ b (mod n). (1)
*) (Понятие сравнимости впервые было введено великим немецким математиком Карлом Фридрихом Гауссом (1777-1855) в его трактате "Арифметические исследования" и является одним из основных понятий теории чисел.)
Число n называют модулем сравнения (1). Например, 35 ≡ 2 (mod 11), так как разность 35 - 2 = 33 делится на 11; аналогично, 25 ≡ -11 (mod 9), так как 25 - (-11) = 36 делится на 9.
Запись a ≡ 0 (mod n) означает тогда, что само число а делится на n, т. е. a = k · n.
Если зафиксировать некоторый модуль сравнения n, то всякое натуральное число с можно единственным образом представить в виде
c = kn + r, (2)
где k - частное от деления на n, а r - остаток, совпадающий с одним из чисел
0, 1, 2, ..., n-1. (3)
Остаток r называют также вычетом числа с по модулю n. Заметим, что запись вида (2), где 0 ≤ r ≤ n-1, допускают не только натуральные, но и любые целые числа. Очевидно, из равенства (2) следует, что с ≡ r(mod n), т. е. всякое число сравнимо со своим остатком (вычетом) по модулю n. Пусть теперь а и b - два произвольных числа, записанные в виде (2):
a = k1n + r1, b = k2n + r2.
Каждый из остатков r1 и r2 - это одно из чисел (3), поэтому их разность может делиться на n лишь в одном случае, когда r1 = r2. Но тогда и разность а - b = (k1 - k2)n + r1 - r2 может делиться на n тогда и только тогда, когда r1 = r2. Отсюда следует, что а ≡ b (mod n) тогда и только тогда, когда числа а и b имеют одинаковые остатки при делении на n.
В теории чисел (см., например, [5]) доказывается ряд свойств сравнений, во многом аналогичных свойствам обычных равенств. Подобно тому, как мы это делаем с равенствами, сравнения по одинаковому модулю можно складывать, перемножать и т. д. (так, перемножив сравнения 17 ≡ 5 (mod 4) и 7 ≡ 3 (mod 4), получим, как нетрудно убедиться, верное сравнение 119 ≡ 15 (mod 4). Вообще, если a1 ≡ b1, а2 ≡ b2, то a1 + a2 ≡ b1 + b2, a1a2 ≡ b1b2.
Значение этих свойств заключается в том, что при рассмотрении вопросов делимости чисел и различных числовых арифметических выражений мы можем входящие в эти выражения числа заменять на другие, сравнимые с ними по данному модулю n; в частности, каждое число может быть заменено своим вычетом. Проиллюстрируем сказанное следующей задачей.
Доказать, что число (1981)k + (1982)k при любом нечетном натуральном k делится на 3.
Замечаем, что 1981 ≡ 1 (mod 3), 1982 ≡ 2 (mod 3). Заменяя в исходном выражении числа 1981, 1982 их вычетами по модулю 3, получаем
(1981)k + (1982)k ≡ 1 + 2k (mod 3).
Следовательно, левая часть сравнения делится на 3 тогда и только тогда, когда на 3 делится сумма 1 + 2k. Для степеней двойки имеем: 22 ≡ 1, 23 ≡ 2, 24 ≡ 1, 25 ≡ 2 и т. д. Вообще, применяя индукцию по k убеждаемся, что 2k ≡ 1 при k четном и 2k ≡ 2 при k нечетном, Таким образом, при нечетном k
1 + 2k ≡ 1 + 2 ≡ 0 (mod 3),
т. е. если k нечетно, то исходное выражение делится на 3.
В разобранной задаче числа 1981 и 1982 могли быть заменены любыми числами а и b, дающими при делении на 3 остатки соответственно 1 и 2. Ни утверждение задачи, ни способ его доказательства от 1 этого не изменились бы. Таким образом, в некоторых вопросах все числа, имеющие один и тот же вычет r по модулю n, и, следовательно, сравнимые между собой по этому модулю, оказываются взаимозаменяемыми. Объединим все их в один класс, обозначаемый r‾:
r‾ = {с | c ≡ r (mod n)}. (4)
Иными словами, класс r‾ состоит из всех тех целых чисел, которые записываются в виде (2). Класс, определяемый равенством (4), называют классом вычетов. Каждому вычету 0, 1, 2, ..., n-1 отвечает свой класс вычетов, так что имеется ровно n различных классов
0‾, 1‾, 2‾, ..., n-1‾. (5)
Ясно, что эти классы попарно не пересекаются и каждое целое число попадает ровно в один класс.
Мы обнаруживаем, далее, что используя операции сложения и умножения чисел, можно производить аналогичные операции и над классами вычетов.
В самом деле, пусть r‾1 и r‾2 - два класса вычетов. Выберем любые два числа из этих классов: a1 ∈ r‾1, a2 ∈ r‾2. Пусть оказалось, что сумма a1 + a2 имеет вычет r, а произведение a1a2 - вычет s:
a1 + a1 ∈ r‾, a1a2 ∈ s‾.
Тогда будем считать, что "сумма" классов r‾1 и r‾2 равна r‾, а их "произведение" равно s‾:
r‾1 + r‾2 = r‾, r‾1 · r‾2 = s‾.
Законность этого определения обосновывается тем, что класс, которому принадлежит сумма а1 + а2 (соответственно произведение а1а2) не зависит от выбора элементов а1 и а2 в классах r‾1 и r‾2.
Поясним данное определение на примере, взяв за модуль сравнения число п-2. В этом случае имеем два класса вычетов - 0‾ и 1‾, а операции над ними выглядят так:
0‾ + 0‾ = 0‾; 0‾ + 1‾ = 1‾ + 0‾ = 1‾ 1‾ + 1‾ = 0‾;
0‾ · 0‾ = 0‾; 0‾ · 1‾ = 1‾ · 0‾ = 0‾ 1‾ · 1‾ = 1‾.
Часто, когда это не вызывает путаницы, в обозначениях классов вычетов опускают черту, записывая их как обычные натуральные числа. В основном тексте книги это делается без специальных оговорок. Выпишем, например, таблицы сложения и умножения классов по модулю 4 в этих упрощенных обозначениях:

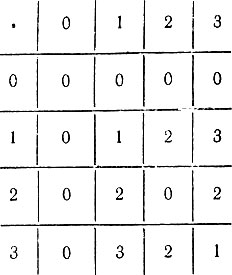
Эти таблицы можно понимать и буквально, считая, что они определяют две операции на множестве {0, 1, 2, 3} - сложение и умножение по модулю 4.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'