3. Кольца и поля

Часто приходится рассматривать множества, на которых определены две операции, например, различные числовые множества, множества многочленов, множества классов вычетов с определенными на них операциями сложения и умножения. Выделяя некоторые свойства этих операций, общие для всех указанных множеств, мы приходим к еще одному важному алгебраическому понятию - понятию кольца.

Кольцом называется (непустое) множество K, на котором определены две операции (сложение и умножение), обладающие следующими свойствами:

1) множество K относительно сложения образует коммутативную группу;

2) умножение ассоциативно: для любых а, b, с ∈ K

3) сложение и умножение подчиняются дистрибутивному закону:

для любых а, b, с ∈ K.

При этом множество K, рассматриваемое лишь относительно операции сложения, называется аддитивной группой кольца.

Приведем некоторые примеры колец.

1. Множество целых чисел с операциями сложения и умножения - кольцо целых чисел Z.

2. Множество многочленов от одного неизвестного с действительными коэффициентами с операциями сложения и умножения многочленов - кольцо многочленов R[X].

3. Множество классов вычетов по модулю n с операциями сложения и умножения классов - кольцо классов вычетов Z_n.

Читателю предлагается проверить выполнимость аксиом кольца в каждом из примеров. Остановимся подробнее на примере 3.

Поскольку операции над классами вычетов сводятся к операциям над числами из этих классов, то свойства ассоциативности и коммутативности этих операций вытекают из аналогичных свойств числового сложения и умножения. То же замечание относится к свойству дистрибутивности. Роль нулевого элемента при сложении играет класс 0‾. Противоположным элементом для класса вычетов r‾ ≠ 0‾ является класс n-r‾. Из определения сложения классов следует, что

В общем определении кольца не содержится требование коммутативности умножения. В том случае, если умножение обладает этим дополнительным свойством, кольцо называется коммутативным. В примерах 1-3 мы имеем как раз коммутативные кольца, а позднее (в приложении 5) познакомимся с важным примером некоммутативного кольца.

Умножение в кольце, как и в группе, является ассоциативной операцией, но другие свойства группового умножения в кольце могут не выполняться. Правда, большинство важных колец содержат единичный элемент относительно умножения (скажем, кольца из примеров 1-3), но и такие кольца заведомо содержат элементы, для которых не существует обратного (необратимые элементы). В любом кольце необратим элемент 0 - нулевой элемент относительно сложения, так как доказывается, что он отличен от единичного и что для любого a ∈ K имеет место:

Как показывают примера 1 и 2, необратимыми могут быть и ненулевые элементы. Так, в кольце целых чисел обратимы лишь 1 и -1, всякое другое n ≠ 0 в кольце Z не имеет обратного, так как 1/n ∉ Z.

Рассмотрим таблицы умножения ненулевых элементов в кольцах вычетов Z₄ и Z₅.

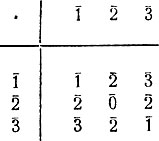
Таблица 19

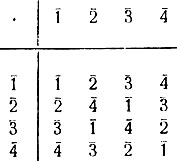
Таблица 20

Таблица 19 показывает, что в кольце могут существовать ненулевые элементы, произведение которых равно нулю: в Z₄ 2‾ · 2‾ = 0‾. Из этой же таблицы видно, что класс 2‾ необратим. Вообще, можно доказать, что ненулевые элементы, произведение которых равно нулю (называемые делителями нуля), всегда необратимы. С другой стороны, таблица 20 показывает, что в кольце Z₅ всякий ненулевой элемент обратим. Кольца с этим свойством имеют особое значение. Примем такое определение.

Коммутативное кольцо с единицей, в котором всякий ненулевой элемент обратим, называется полем.

Множество ненулевых элементов поля относительно умножения образует в силу определения поля коммутативную группу, которая называется мультипликативной группой поля.

Простейшими примерами числовых полей являются поле рациональных чисел Q и поле действительных чисел R (разумеется, относительно операций сложения и умножения чисел). Полем, как ясно из предыдущего, является и кольцо Z₅. Вообще, можно доказать, что при любом простом р (и только в этом случае) кольцо вычетов Z_p является полем. Оно называется полем вычетов по модулю р. В таблице 21 указаны элементы, обратные к ненулевым элементам поля вычетов Z₇.

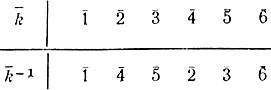
Таблица 21

Поля вычетов Z_р являются простейшими примерами конечных полей. В алгебре доказывается, что в произвольном конечном поле число элементов q всегда есть степень простого числа: q = pⁿ. Справедливо и обратное утверждение: для любого q, являющегося степенью простого числа, существует поле с q элементами.

Конечные поля часто называют полями Галуа (их обозначают GF(g)); важное их свойство, используемое, в частности, и в теории кодирования, состоит в следующем:

Мультипликативная группа поля Галуа является циклической группой порядка q-1.

Образующий элемент мультипликативной группы поля Галуа называют примитивным элементом. Так, в поле Z₇ примитивным элементом является класс вычетов 3‾. Действительно, его степени

исчерпывают все ненулевые элементы поля.

Заметим, что класс 2 не является примитивным элементом в Z₇, так как среди его степеней нет, например, класса В. В то же время имеется очень много простых чисел р, для которых элемент ‾2 примитивен в Z_р. Так обстоит дело в полях Z₃, Z₅, Z₁₁ и т. д. В теории чисел известна следующая до сих пор не решенная задача:

Бесконечно ли множество тех простых чисел р, для которых ‾2 является примитивным элементом в Z_p?

Интересно, что с ответом на этот вопрос связано решение некоторых проблем теории кодирования.

В заключение определим еще одно важное понятие, связанное с кольцом, - понятие идеала.

Подмножество I кольца K называется его (двусторонним) идеалом, если оно само является кольцом относительно операций на K и если для любых элементов а ∈ K и b ∈ I оба произведения аb и bа принадлежат I.

Так, множество четных чисел есть идеал кольца Z. Читатель легко проверит, что и вообще всякое множество чисел, кратных какому-нибудь числу k, является идеалом кольца Z.

Рекомендуем читателю найти идеалы колец вычетов Z₅, Z₆, Z₈ и кольца многочленов R[X].