Математика

Во времена молодости авторов этой книги - в 30-е годы - была популярной "Неаполитанская тарантелла". В летние месяцы из открытых окон слышались звуки грампластинок, проигрывавшихся на модных тогда патефонах, и при этом часто раздавались слова песенки: "Человеку знать не надо, что такое человек ...".- Далекое, милое прошлое. Ныне человек очень хочет знать: что же такое он есть, что есть жизнь, что есть мысль, что есть разум? И бросает на добывание этого знания мощный арсенал современной науки. И в том числе - математику.

Громадное место математики в человеческом познании отмечалось многими мыслителями. "В каждом знании столько истины, сколько есть математики", говорил И. Кант. "Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой" (Леонардо да Винчи). "Книга природы написана на языке математики" (Г. Галилей). "Зрелость науки обычно измеряется тем, в какой мере она использует математику" (Л. Стивене). "Если вы в состоянии измерить и выразить то, о чем вы говорите, то вы кое-что об этом знаете; но если вы не можете измерить это и выразить в числах, ваши знания скудны и неудовлетворительны" (лорд Кельвин). "Цивилизация насыщена идеями числа и измерения. Даже явления повседневной жизни неразрывно связаны с ними" (Ю.Кендал).

Одно из решающих достоинств математики, благодаря которому математизация знания прогрессивна, неизбежна и желательна, - это способность математики служить источником моделей для отношений, процессов и событий, наблюдающихся в окружающем нас мире. Разумеется, полного соответствия между математическими моделями и эмпирическими "переменными" реальности не бывает; для моделирования одних явлений математика пригодна лучше, для других - хуже, для третьих надо создавать какие-то новые математические теории, для четвертых - и создавать нечего: для них математика может быть лишь сугубо вспомогательным орудием. Но здесь для нас важен один фундаментальный тезис: человек не "изобретает" - не навязывает природе - математику; природа "математична" потому, что, как заметили английские астрофизики Дж. Джине и А. Эддингтон, человек создает математику "под природу": "математическое одеяние скрывает под собой мир".

Однако степень добротности математического отражения тех или иных феноменов действительности различна. В известном труде Д. Гильберта и П. Бернайса подчеркивается, что "в науке - если не всегда, то по преимуществу - мы имеем дело с такими теориями, которые отнюдь не полностью воспроизводят действительное положение вещей, а являются лишь упрощающей идеализацией этого положения, в чем и состоит их значение" [17, с. 25]. Не всегда эта "упрощающая идеализация" имеет, так сказать, знак "плюс"; подчас - и "минус". По сути дела упрощение - это цена формализации.

Понятие формализации нуждается в особом разъяснении. В самом общем смысле формализация есть уточнение содержания посредством фиксации его формы, понимаемой в самом широком смысле. Например, к формализации в такой ее трактовке можно отнести выработанные в античной скульптуре каноны пропорций обнаженного человеческого тела или современные знаки регулирования дорожного движения. Однако, говоря о формализации, в кибернетике имеют в виду такую фиксацию формы, которая происходит средствами математики и логики. Подобная формализация - будем называть ее математической формализацией - может происходить на двух разных уровнях, различающихся степенью полноты, глубины, исчерпанности уточняемого содержания. Менее глубокий уровень связан с использованием математики как таковой. Формализация на этом уровне производится обычными математическими методами, без строгого "препарирования" самого математического языка. На более глубоком - наиболее строгом - уровне формализации язык (и система понятий) математики используется в его формальном виде, обычно связанном с использованием столь же строго построенной (формализованной) логики. Формализация в этом смысле - это представление соответствующей содержательной области в виде формальной системы - алгоритмической схемы или исчисления как системы правил порождения формальных объектов. В последующем изложении, говоря о формализации, мы будем иметь в виду главным образом математическую формализацию, хотя в ряде случаев будут приниматься во внимание и другие смыслы этого термина. Это объясняется тем, что многие теоретические оценки данного познавательного приема справедливы для всех отмеченных выше смысловых оттенков.

Далеко не всякую содержательную область даже ценой существенных усилий можно формализовать таким образом, что упрощение - как цена, выплаченная за формализацию, - не окажется чрезмерным, иначе говоря, таким, что вся работа по построению математической модели (алгоритмического описания изучаемого процесса, формальной системы, выражающей данную содержательную область и пр.) не утратит смысл.

Имея в виду формализацию в ее наиболее глубоком виде, известный специалист по математической логике и основаниям математики С. К. Клини говорил: "Если рассматривать картину полностью, то имеются три отдельные и отличные друг от друга "теории": (а) содержательная (informal) теория, формализацией которой служит формальная система, (b) формальная система или предметная теория и (с) метатеория, в которой описывается и изучается эта формальная система" [18, с. 63]. Формальные системы, изучаемые в метатеории, обычно выбираются так, что они служат моделями для частей содержательной дисциплины (теории) и получаются из этих частей путем формализации. "Формализация сводит развитие теории к форме и правилу. Она устраняет всякую неопределенность в отношении того, что такое предложение теории или что такое доказательство в ней. И вопрос о том, не приводят ли к противоречию те методы, которые были формализованы, а также другие вопросы о действии этих методов должны изучаться в метатеории посредством методов, не подверженных тем же сомнениям, что и методы первоначальной теории " [там же, с. 62].

В математике, если в ней используется строгая формализация теории, предполагается - на чисто знаковом, или синтаксическом, уровне таковой - полная абстракция от смысла. Это имеет огромное значение для цикла дисциплин, объединяемых термином "кибернетика"; требования машинной реализации как раз обусловливают элиминацию смыслов выражений формализованного языка соответствующей математической (кибернетической) модели; современная машина, в отличие от человека, ничего не понимает, и неформальное оперирование со смыслами для нее недоступно.

Пытаясь провести границу между тем, что кибернетика может, и тем, что она не может, нередко ссылаются на известные результаты математической логики и теории алгоритмов, говорящие о внутренней ограниченности формализации. Речь, прежде всего, идет о знаменитой теореме К. Гёделя о неполноте формализованной арифметики (1931 г.). Согласно этой теореме, любая непротиворечивая формальная логико-математическая система, оперирующая конструктивными объектами (об этом понятии ниже), в которой выразима арифметика натуральных чисел, содержит в числе своих предложений такие формулы, которые в ней не могут быть доказаны (и не могут быть опровергнуты), - содержит неразрешимые предложения. Ссылаются и на другой математико-логический результат - на теорему А. Чёрча (1936 г.) о том, что для логики предикатов принципиально невозможно построить общий метод, позволяющий распознавать, доказуема ли произвольная формула этой логики или нет.

Методологическое значение этих результатов состоит в том, что они обнаружили существование так называемых неразрешимых массовых проблем. В логике и теории алгоритмов под массовой проблемой понимают бесконечный класс научных задач, характеризуемый единым условием, для которого ставится вопрос о построении регулярного предписания (алгоритма), задающего общий метод решения конкретных задач этого класса. Теоремы Гёделя, Чёрча, многочисленные другие результаты, полученные в логике и математике, показали, что существуют такие массовые проблемы, для которых построение такого рода алгоритмов в принципе невозможно.

Открытие феномена алгоритмической неразрешимости, теоремы Гёделя и Чёрча свидетельствовали о том, что формализация и алгоритмизация внутренне ограничены. Об этом говорили также такие результаты, как обоснование тем же Гёделем невозможности доказательства непротиворечивости формальной логико-математической системы средствами, формализуемыми в той же системе, и доказательство А. Тарским того, что понятие истинности, применяемое к предложениям формальной системы, невыразимо средствами самой этой системы.

Из этих результатов следует, что математика в целом не может быть формализована. А это означает, что завершенная формализация и алгоритмизация не "проходят" для любой науки, использующей математический аппарат (во всяком случае, аппарат, содержащий арифметику натуральных чисел) . А какая наука не предполагает арифметики?!

Следует, однако, иметь в виду, что обнаруженная ограниченность есть ограниченность формализации и алгоритмизации как неких "универсальных", "глобальных" методов. Она никоим образом не бросает тень на значение формализации и алгоритмизации в конкретных областях и проблемах. Более того, сами упомянутые результаты не следует переоценивать в плане их ограничивающей силы. Ведь, например, если данная массовая проблема алгоритмически неразрешима, может оказаться разрешимой более узкая проблема, получающаяся из данной введением дополнительного условия.

Гносеологическим источником рассматриваемой ограниченности является неизбежное огрубление, "остановка движения", присущие всякой формализации и алгоритмизации. Дело в том, что содержание любой области, подлежащей формализации и алгоритмизации, должно быть обработано так, чтобы оно могло быть представлено так называемыми конструктивными объектами, каковыми являются элементы алгоритмов и исчислений. Конструктивные объекты - это объекты, изменениями которых мы можем пренебречь, считая их абсолютно "жесткими", однозначно различаемыми и отождествляемыми. Формализация и алгоритмизация - эти процедуры обычно тесно связаны между собой - возможны и плодотворны лишь в той мере, в какой представление содержания некоторой области с помощью конструктивных объектов является действительно возможным и оправдывается целями исследования или практической деятельности.

Ясно, однако, что выражение содержания с помощью конструктивных объектов есть огрубление. Оно-то и обусловливает ограниченность метода построения формальных систем и алгоритмов. "Остановка" движения, или, лучше сказать, втискивание его в жесткие рамки, - вот в чем источник того своеобразия "формальных процедур", которое выражается в теоремах Геделя, Чёрча и других подобных результатах.

Но ведь в реальном мире движение ничем не ограничено. В природе нет особого царства "формальных процедур", отделенных от движения материи и процессов мышления. Правда, в ней есть процессы, в которых более, чем в других, выражена "формальная" сторона. Если брать мир живого, то таким процессом можно считать передачу наследственной информации: "язык наследственности" в некотором роде похож на формализованные языки и алгоритмы науки. Во всяком случае, его нетрудно представить формальными средствами, выразить в виде некоторого научного языка. Но, конечно, сам-то он не формален: элементы этого "языка" - материальные носители наследследственной информации - взаимодействуют друг с другом, с ними происходят случайные изменения (мутации), они играют активную роль в эмбриогенезе и т.д. Тем более неформальны другие процессы и превращения в мире живого. На живые организмы неверно смотреть как на некие "реализации" каких-то формальных систем и алгоритмических процедур (хотя некоторые структуры и функции живого с определенным приближением допускают такое представление). В этом смысле они резко отличаются от создаваемых ныне человеком цифровых машин и автоматов: ведь эти машины предназначаются именно для реализации формальных процедур.

Но не только природа "неформальна". Неформально и человеческое познание, взятое в целом. Неформальны многие процессы познания, его стороны и т. п. Нельзя чрезмерно сближать (как это делает С. Л ем в своей книге [19]) любые "теоретические структуры" науки, т. е. любое научное построение, любой процесс научного познания, с формальными системами, с построением исчислений, с "формализмами" и алгоритмизацией. На деле "теоретические структуры" в большинстве случаев вовсе не являются "формальными структурами".

Следует различать содержательный и формальный аспекты знания. Наука развивается прежде всего как содержательное знание. Содержательное знание - это знание неформализованное, неалгоритмизованное, использующее данные экспериментов и наблюдений, выдвигающее, обосновавшующее и опровергающее естественно-научные гипотезы, пользующиеся догадками и апеллирующие к научной интуиции. Построение различных формальных систем, исчислений и т. п. есть лишь одна из сторон развития знания. При этом, если отдельно взятая формальная система или алгоритм - формальны, то построение этой системы или алгоритма, переход от одной формальной системы или алгоритма к другой системе или другому алгоритму и т. д.-это, как правило, неформальные процессы. Такой подход очень важен: обычно если определенная часть содержания, подлежащего формализации, не "втискивается" в данную формальную систему, то может быть разработана другая система: такая, в которой будет уже более полно выражаться изучаемое содержание. Например, те индивидуальные задачи, к решению которых не дает доступа некоторая массовая проблема, могут алгоритмически решаться в рамках более узкой или попросту иначе поставленной массовой проблемы.

Человеческое знание в целом - не формально, и для него не просто не действуют (сказать так - было бы неверно), а не имеют смысла те ограничения, о которых говорит дедуктивная логика и теория алгоритмов. Причина этого состоит в том, что знание в его целом является развивающимся знанием и что оно способно отображать не только "жесткое", но и изменчивое, текучее, подвижное, не только "вещи", но и "процессы". Конечно, познание "текучего", отображение движения происходит всегда путем его "остановки", но эта остановка снимается в ходе развития знания, в частности - но не только! - в ходе перехода от одних формализации к другим, более адекватно отображающим содержание.

После всего сказанного мы можем получить ответ на вопрос, подвержены ли ограничениям, установленным в логике и теории алгоритмов для формальных систем и алгоритмических процедур, кибернетические системы. Да, подвержены, если кибернетические системы (например, реализованные в виде цифровых автоматов) моделируют сложившееся знание, представленное или представимое в виде исчислений и алгоритмов. Нет, - а точнее, "не совсем" - подвержены, если такие системы наделены способностью получать новое знание, причем получать его не только "дедуктивным" путем, но и путем некоторого аналога человеческой интуиции и обобщения. Подвержены, если рассматриваются кибернетические системы с "жесткими" программами. Могут быть не подвержены ("не совсем" подвержены), если речь идет об "эволюционизирующих" автоматах, т. е. об автоматах, погруженных в некоторую "среду" и способных изменять программы своей работы в "нужном" направлении в результате взаимодействия с этой средой.

Самоорганизующиеся и обучающиеся системы, доступ к исследованию и конструированию которых упорно ищут в кибернетике, не обязательно должны "страдать" от ограничений, которые действуют для формальных систем. Все зависит от того, насколько успешной будет передача этому (пока еще гипотетическому) "виду" "теоретических машин" (как назвал их Лем) способности развивать знание. Но это - вопрос реализации, а не принципиальной возможности или невозможности, правда, такой вопрос - и к этому мы еще вернемся, - который сам может носить принципиальный характер. В принципе такой "вид" будет столь же мало подвержен ограничениям формальных систем и алгоритмов, как и природные процессы, как реальное развивающееся человеческое знание. Это следует из результатов теоретической кибернетики, доказавших возможность построения самоорганизующихся и самообучающихся кибернетических систем и "размножающихся" автоматов. Функционирующий мозг (о котором можно сказать, что это "орган движения" человеческой жизни: в прошлое нас уводит память, в будущее - надежда) создает "модели" действительности, данные человеку в его внутреннем мире. Они реализуются в виде сложной мозаичной системы связей между множествами активных элементов мозга - нейронов; последние сами представляют собой сложнейшие системы, организация которых необходимо участвует в общей нейродинамике. Однако когда человек обнаружил, что не все модели действительности могут быть непосредственно "воссозданы" в его внутреннем мире, он стал материализовать их во внешнем материале. Такое "продолжение" мозга в огромной степени расширило возможности человека, о чем мы еще будем говорить.

Для построения "вещественных" (внешних) моделей необходимо произвести в данной содержательной области формализацию. Если отойти от строгого толкования этого понятия (как это делается в математической логике), очерченного нами выше, и подойти к нему более просто (и поэтому менее формально), то можно сказать, что цель формализации - получение ответов на содержательные вопросы без привлечения сложных мыслительных актов; иначе говоря, в какой-то степени замена размышлений вычислениями ("когда описание открывает путь для измерений, дискуссия вполне заменяется вычислениями", сказал А. Стивене).

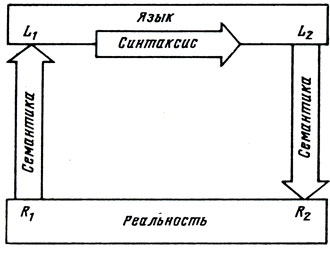
Рис.2

Пусть, например, в языковой модели (рис. 2) элемент реальности R₁ кодируется языковым объектом L₁. Преобразование L₁ в L₂ производится в виде вывода следствия L₂ из основания L₁. Можно считать, что L₂ декодируется B L₁. Совокупность преобразований R_j → L_j (i = 1, 2, 3,...) и обратных преобразований составляет семантику языка (семантика -смысловая сторона языковой системы, ее слов и выражений), а совокупность преобразований L_i → L_j (i, j = 1, 2, 3,...) - его синтаксис (под синтаксисом обычно понимают систему правил сочетания слов и построения предложений данного языка) . В математической теории - ее языке - синтаксис считается полностью формализованным в том случае, когда построено исчисление либо алгоритм (алгоритмическая схема), скажем "машина Тьюринга", производящий преобразование L_i → L_j; вместо "машины Тьюринга" может быть использована любая другая алгоритмическая схема или исчисление, например, нормальные алгорифмы Маркова [13] или аппарат формальных нейронов Мак-Каллока - Питтса; (см. [20]). Язык считается неполностью формализованным, если преобразования вида L_i → L_j производятся человеком; за счет четкой стандартизации языка, в предположении абстракции потенциальной (принципиальной) осуществимости "научить" этим преобразованиям можно и машину. Важно тольг ко - и в этом состоит строгость формализации, - чтобы не возникало сомнений относительно правильности преобразований: чтобы они были полностью "принимаемы" машиной. В проверке формализации на строгость состоит назначение метатеории (метатеорией математики, или метаматематикой, Д. Гильберт называл теорию, изучающую формализованные доказательства математики).

Переход от теории к метатеории (а от нее - к метаметатеории и т. п.) можно сравнить с подъемом по ступеням лестницы. Неграмотному человеку невозможно объяснить, скажем, в чем заключается теория относительности: надо начинать с обучения чтению и письму и с арифметики, а затем, поднимаясь со ступеньки на ступеньку, дойти до желаемого предмета. Точно так же невозможно "голыми руками" построить ракету: необходимо создать орудия труда и пройти длинный путь технического прогресса. Примерно та же картина начинает ныне складываться в научных теориях, структуры которых образуют иерархические системы понятий; формализованные языки служат материальным телом ступенек упомянутой "научной лестницы".

Принято считать, что средствами математики исследователи во всех случаях получают более точные данные там, где раньше они довольствовались весьма приблизительными результатами. Однако в действительности так бывает далеко не всегда. Как верно подчеркнул Ю. А. Шрейдер, "точность доказательства должна соответствовать точности утверждения" [21]. Это значит, что точными рассуждениями и методами нельзя вывести либо обосновать истины, имеющие чрезмерно общий и расплывчатый характер. Для выражения такого рода истин (хотя бы в какой-то его части) в последние годы, главным образом в работах Л. Заде [22 - 24] и его последователей, начал разрабатываться аппарат, получивший название теории расплывчатых (размытых, нечетких) множеств. Так эта теория названа потому,что центральным ее понятием является понятие расплывчатого множества. Отличие расплывчатого множества (класса, объема понятия) от обычного "жесткого" множества состоит в том, что в то время как произвольный элемент х рассматриваемой предметной области X может либо (вполне) принадлежать данному "жесткому" множеству М (т. е. имеет место х ∈ М, либо (всецело) не принадлежать ему (х ∉ М), расплывчатое множество М_распл допускает принадлежность элементов множеству различной степени, оцениваемой на бесконечной шкале действительных (или рациональных) чисел от 0, означающего полную непринадлежность, до 1, выражающей полную принадлежность (разумеется, оценка может производиться и на части чисел интервала [0, 1], в том числе и на конечной). Если, скажем, М_распл есть множество смелых людей (X - люди), то высказывание "NN смелый человек" может утверждать отнесение человека NN к расплывчатому множеству "смелых людей" с оценкой, скажем, 0,73. Такие высказывания по Заде можно записать как μх (х ∈ М), где и играет роль "оператора расплывания"; этот оператор представляет собой функцию, значения которой берутся из области [0, 1]. Обозначив класс "смелых людей" через Cμ_распл, мы будем иметь: μ х (х ∈ С_распл) = 0,73.

По мысли Л. Заде, теория расплывчатых множеств при анализе систем, в которых существенная роль принадлежит суждениям и решениям человека (такие системы данный автор назвал "гуманистическими"), может оказаться гораздо эффективнее, нежели классическая математика с ее идеей математической непрерывности или даже конечная математика, непосредственно "переводимая" на цифровой язык ЭВМ.

К гуманистическим относятся не только правовые, административные, экономические и т. п. структуры, но и мыслительные процессы и вообще все те системы и процессы, на поведение которых сильное влияние оказывают действия, решения, суждения, эмоции людей. Согласно замыслу Л. Заде и его школы, нечеткие множества и соответствующая им логика могут найти полезное применение при количественном анализе особо сложных систем, к которым, несомненно, относятся гуманистические: "Жертвуя точностью перед лицом ошеломляющей сложности, естественно изучить возможность использования так называемых лингвистических переменных, т. е. переменных, значениями которых являются не числа, а слова или предложения в естественном или формальном языке" [23, с. 10].

Л. Заде с большой силой провозгласил принцип, названный им принципом несовместимости: высокая точность невозможна для систем большой сложности (впрочем, этот принцип, не называя его таким образом, сформулировал уже такой "первопроходец" кибернетики, как Дж. фон Нейман). Теория лингвистических переменных, по замыслу ее автора, и должна служить средством учета этого принципа при формализации "больших" структур и сложных процессов принятия решений. Разработчики теории нечетких множеств утверждают, что благодаря заложенному в данной теории обобщающему потенциалу (нечеткое множество представляет собой более общее понятие, чем четкое, так как последнее выступает в качестве частного случая первого, а именно, такого случая, когда интервал [0, 1] сводится к двучленному множеству { 0, 1} ) большая часть математического аппарата,используемого ныне для анализа и синтеза сложных систем управления и принятия решений, может быть приспособлена для оперирования с лингвистическими переменными. Энтузиасты новой теории считают, что "нечеткостный" лингвистический аппарат может найти применение при описании многих явлений, которые настолько сложны, что не поддаются привычному "точному" выражению.

Лингвистическая переменная описывается набором (х, Т(х), U, G, M), где х - название переменной; Т(х) - совокупность ее лингвистических значений (так называемый терм-множество переменной х); U - универсальное множество (предметная область) ; G ~ синтаксическое правило, порождающее термы множества Т(х); М- семантическое правило, которое каждому синтаксическому значению переменной х ставит в соответствие его смысл М (А) , причем М (х) обозначает нечеткое подмножество множества U. Например, "возраст" - лингвистическая переменная, если она принимает значения "молодой", "не молодой", "очень молодой", "старый", "не очень старый" и т.п. Значения лингвистической переменной графически изображаются в виде площадки с нечетко очерченными границами. При этом числовая переменная с тем же названием ("возраст", принимающая числовые значения 1, 2, 3, ... , 100; эти числовые значения обозначают число лет; рассматриваются люди не старше 100 лет) называется базовой переменной лингвистической переменной "возраст". Тогда значение лингвистической переменной "молодой" можно истолковать как название некоторого нечеткого ограничения на значения базовой переменной. Его можно охарактеризовать функцией совместимости, которая каждому значению базовой переменной ставит в соответствие число из интервала [0, l], символизирующее совместимость этого значения с нечетким ограничением. На рис. 3 показан пример графика функции совместимости лингвистического значения "молодой" относительно базовой переменной "возраст". Как видно из рисунка, для численных значений переменной "возраст" 20, 25 и 35 с нечетким ограничением "молодой" функция совместимости принимает значения: 1; 0,9 и 0,6, соответственно.

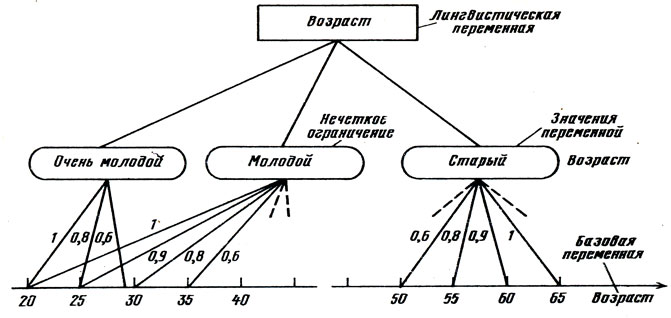
Рис.3

Было бы неверно думать, что теория нечетких множеств положила начало математическому описанию неопределенных образований и нежестких (нечетких, расплывчатых) объектов. Не говоря уже о теории вероятностей, научный аппарат, необходимый для такого описания, задолго до соответствующих работ Заде возник в математической логике (теория многозначных и бесконечнозначных логических систем) и алгебре (теория алгебраических систем). Но теория нечетких множеств ввела исследование нечеткостей различного рода в более широкий теоретический и прикладной контекст и придала им резко выраженную кибернетическую направленность. В настоящее время помимо теории нечетких классов (множеств) в той или иной степени разработаны соответствующая нечеткая логика, включая нечеткие отношения, лингвистические вероятности, теорию игр в нечетко определенной обстановке, теорию распознавания нечетких образов; развиваются теория расплывчатых алгоритмов и теория нечетких автоматов и тл. Математическая логика составляет для этих исследований надежную базу и - во многих случаях - доставляет более совершенный математический аппарат, нежели тот, которым пользуется Л. Заде и представители его школы.

В качестве упрощенной иллюстрации того, как можно определить новое нечеткое понятие с помощью более простых или более знакомых расплывчатых понятий, Л. Заде в работе [23] рассматривает пример нечеткого подмножества множества людей (см. блок-схему на рис. 4). Заде полагает, что, модифицируя нечеткие множества, входящие в определение соответствующего понятия, при помощи таких неопределенностей, как "очень", "более или менее", "чрезвычайно" и т. п., и допуская ответы типа да/μ или нет/μ, где μ - оценка ответов "да" и "нет" числами из интервала [0, 1], а косая черта означает соответствие оценки ответу, можно получить определение понятия, точнее выражающее его содержание.

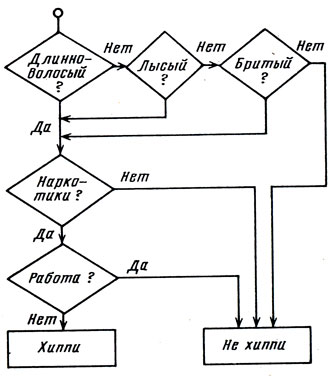
Рис.4

Разумеется, перспективы описанного "нечеткостно-лингвистического" подхода к анализу и синтезу сложных систем во многом еще не ясны. Его создатели считают, что "он вполне может оказаться шагом в нужном направлении, т. е. в направлении меньшего увлечения точным количественным анализом и большего допущения важной роли неточности в мышлении и восприятиях человека. Мы убеждены в том, что, приняв это направление, мы сможем больше продвинуться в понимании поведения гуманистических систем, чем это возможно в рамках традиционных методов" [23, с. 146].

Однако теория нечетких объектов - только один из путей изучения "гуманистических" систем на новых путях. В качестве других возможных направлений можно назвать использование вероятностной и индуктивной математической логики, "байесовский" подход к языку, идею которого выдвинул В. В. Налимов [25], теорию тезаурусов, оплодотворенную понятием семантической информации по Ю. А. Шрейдеру [26, 27], особенно если ее сочетать с той или иной теорией расплывчатости или неопределенности (ср. идеи, высказанные в книге [28] и др.). Не останавливаясь на этом подробнее, мы отсылаем читателя к соответствующей литературе.