Общие требования к алгоритму

При разработке программы следует учитывать, что во время ее выполнения не должны быть превышены допустимый объем памяти ЭВМ и допустимое время решения задачи. Поэтому к алгоритму можно, по-видимому, предъявить четыре основных требования.

1. Выделение информации первостепенной важности. Об этом уже было сказано выше, что соответствует рекомендациям К. Шеннона, сделанным еще в 1949 г. Если программе не дано отличать существенное от несущественного, если, например, из всей массы имеющихся на данный момент возможных ходов шахматная программа ЭВМ не может выделить ходы первостепенной важности или, иначе говоря, ходы, имеющие смысл, то остается только один неэкономичный путь - перебор всех ходов.

Мне приходилось слышать мнение некоторых специалистов по этому вопросу, что, де мол, ничего плохого в этом нет. Правда, признают они, человек мыслит, выделяя информацию первостепенной важности, но означает ли это, что ЭВМ должна слепо подражать человеку? Человек - это человек, а ЭВМ - это ЭВМ, и она может перерабатывать информацию по-своему. Автор готов был бы поверить в искренность этих рассуждений, если бы человек перебирал всю информацию, а эти специалисты в своих программах для ЭВМ нашли бы хитрый способ выделения важной информации. Но так как дело обстоит наоборот и в этих программах используется примитивный метод, сокращающий лишь длину вариантов в дереве полного перебора, то теорию об особом методе мышления ЭВМ следует рассматривать как попытку оклеветать ни в чем неповинную ЭВМ, которая, увы, себя защитить пока не может. Рекомендация Шеннона на сей счет представляется безукоризненной.

Добавим, что способность программы выделять информацию первостепенной важности, вероятно, находится в прямой зависимости от правильно выбранной цели игры.

2. Ограничение длины вариантов перебора. Против этого требования уже никто не может возражать. ЭВМ, как и любое другое устройство по переработке информации, в том числе и мозг человека, имеет ограниченные быстродействие и объем памяти. Между тем решение должно быть принято в ограниченный срок и с имеющейся ограниченной памятью ЭВМ. Единственный способ принять решение в этих условиях состоит в ограничении длины вариантов перебора. Этот метод применяется во всех играющих шахматных программах.

Здесь еще раз отметим важность первого требования о выделении информации первостепенной важности. Есть надежда, что перебор информации, лишь имеющей смысл, приведет к экономии и времени и памяти, т. е. ограничение длины вариантов перебора станет слабее. Конечно, это будет лишь в случае, если отбор важной информации не потребует существенного расхода времени и памяти.

Надо полагать, что и здесь успех зависит от выбранной цели игры.

3. Выделение и экономное исполнение повторяющихся операций. В каждой задаче кроме ситуаций оригинальных неизбежно встречаются ситуации повторяющиеся. Например, в шахматах после того, как четыре с половиной столетия назад окончательно сложились правила игры, повторяющейся операцией является передвижение данной фигуры с одного поля на другое поле свободной от фигур доски. Из партии в партию эта стандартная операция в течение веков переходит в одном и том же застывшем состоянии. Ясно, что эта стандартная операция должна выделяться и исполнение ее программой должно происходить наиболее экономно.

Более или менее очевидно, что программа должна выделять эти повторяющиеся стандартные операции и исполнять их простейшим и скорейшим образом. Это будет способствовать экономному расходованию и времени и памяти ЭВМ, т. е. в конечном итоге более глубокому решению задачи. И здесь успех находится в прямой связи с выбранной целью игры. Если цель игры не обеспечивает выделения стандартных операций и их простейшего исполнения, значит цель выбрана неудачно.

4. Не пересчитывать уже сосчитанного (если достаточен объем памяти) ... Действительно, пусть специалист пришел к выводу, что только сложный, хитроумный алгоритм обеспечит хорошее решение задачи; пусть также до этого действовали сравнительно простые программы, с помощью которых достигались, правда, слабые результаты, но все же какие-то результаты. Естественно, новый сложный алгоритм встречается в штыки и со всех сторон неизбежны возражения: алгоритм сложен, программа будет работать медленно и никакой памяти не хватит, ибо получение решения потребует большого объема работы ЭВМ.

Между тем, это требование в ряде случаев позволяет избежать указанных недостатков. Программа должна отделять информацию, которая меняется, от информации, которая осталась неизменной. Если программа эту измененную информацию способна выделять, то опасаться сложной программы нечего.

Есть надежда, что при этой программе потребуются время и объем памяти, соизмеримые с простой программой (когда неизменяемая информация не выделяется), а решение будет более точным. Однако эту рекомендацию нельзя принимать безоговорочно. Если информация занимает большой объем памяти, а восстановление этой информации - дело простое, то может оказаться выгодным не запоминать, а возобновлять информацию, это зависит от конкретных обстоятельств.

Таковы, на взгляд автора, четыре основных требования к алгоритму.

Посмотрим теперь, как обеспечивает реализацию этих требований цель шахматной игры по Шеннону.

1. В США 1970-1973 гг. Ассоциацией вычислительной техники были проведены чемпионаты шахматных программ для ЭВМ. Профессор М. Ньюборн (под его руководством проходил первый чемпионат 1970 г. в Нью-Йорке) в своем обзоре первых двух чемпионатов указывал, что все программы, участницы турнира, были сделаны по Шеннону (они отличались лишь по языку программирования, типу ЭВМ и т. п.). Таково свидетельство очевидца.

Если за 22 года не удалось избавиться в шахматных программах от "полного" перебора ходов, невыгоды которого еще в 1949 г. были отмечены самим К. Шенноном, значит есть какая-то очень уважительная причина, препятствующая продвижению вперед. И эта причина (по мнению автора) - неудачная цель игры, которая связана со всей доской, с массивом 8*8. Ни одно поле этого массива не выделяется поставленной целью, поэтому элементарные системы управления (фигуры) не имеют своих конкретных, индивидуальных целей. Цель, связанная со всем массивом 8*8, не дает никаких рекомендаций элементарной системе в отношении направления движения. Между тем фигура только и умеет, на первый взгляд, что двигаться, а раз рекомендаций на сей счет нет, значит надо перебирать ее движения во всех направлениях, т. е. необходим полный перебор возможных ее передвижений.

Мы видим, что ошибочная цель игры, не обеспечивающая конкретности цели и (в этом понимании) осмысленности действий элементарных систем, неизбежно приводит к слабым результатам.

Добавим, что если и были сделаны попытки избавиться от перебора всех ходов (это стало ясно после первого шахматного чемпионата мира среди ЭВМ в Стокгольме в августе 1974 г.), то они не дали лучших результатов, ибо цель игры не содействовала успешному выделению ходов, имеющих смысл.

2. Ограничение длины вариантов перебора реализуется примитивно. Ограничения по сути дела нет, а просто-напросто, когда время счета истекает, перебор прерывается и производится оценка его вариантов. Программа следит при этом, чтобы варианты были равной длины и в этом есть некоторая маскировка: ограничивается не время перебора, а длина перебираемых вариантов в полуходах (например, в программе-победительнице чемпионатов США длина перебираемых вариантов, как правило, равна четырем полуходам). Однако это ограничение (подравнивание длины вариантов) в основном связано с ограничением времени перебора: в пределах этого времени надо считать все, а затем во всех вариантах (кроме некоторых) счет прекращать.

Представим себе садовника, который, подравнивая ветки деревьев по заданному шаблону, формально исполнял бы инструкцию и удлинял бы ветки, привязывая к ним прутики, чтобы все они были равной длины. Вряд ли эта бессмысленная работа была бы встречена с одобрением. Многие программисты заставляют ЭВМ так работать и утверждают при этом, что все это разумно.

Итак, и второе требование к алгоритму (при полном переборе вариантов), видимо, выполняется неудовлетворительно.

3. С выделением и исполнением повторяющихся

стандартных операций дело обстоит не лучше. Когда неизвестно, в каком направлении фигура должна передвигаться, и приходится перебирать все возможные передвижения, то стандартной операцией становится перемещение фигуры за один полуход. Стандартная операция становится очень простой, в то время как стандартизировать надо предельно сложные операции; именно в этом случае и будет получена наибольшая выгода. Стандартизация предельно простых операций существенных вы год дать не может.

Поэтому при определении цели игры по Шеннону, цели, связанной со всем массивом 8X8, по существу, не удается выполнить и этого требования.

Посмотрим, как же обстоит дело с последним, четвертым требованием.

4. Здесь автор должен быть осторожным, так как не знает тонкостей действующих программ. Может быть, удается избежать повторных расчетов, может быть, нет. Думаю, что не удается, но уверенности на этот счет у меня нет. Да это и несущественно. Уже ясно, что, когда цель игры связана со всей доской, с массивом 8*8, требования, предъявляемые к алгоритму, в основном не могут быть удовлетворены.

А теперь обратимся к тому случаю, когда цель игры иная; выясним, как обстоит дело, когда типовая цель игры - выигрыш материала. Рассмотрим снова выполнение всех четырех требований.

1. Ясно, что цель эта неточная, паллиативная (так же, как и в случае цели по Шеннону). Точная цель состоит не в выигрыше вообще, а в выигрыше короля. Основное преимущество этой простой цели (выигрыш материала) состоит в том, что она связана не только со всей доской (массивом 8*8), но непременно и с полями доски. Это позволяет иметь цели игры как для совокупности элементарных систем (цель, связанную с массивом 8*8), так и для элементов совокупности (цели, связанные с отдельными полями массива 8*8). По типу Цели всей системы и отдельных ее элементов одинаковы, по конкретной форме - различны. Позднее читателю станет известно, что кроме отдельных полей и всего массива 8*8 есть еще зоны игры, охватывающие некоторый комплекс полей и фигур. В зонах также есть свои конкретные цели игры того же типа, что для отдельных полей и для массива 8*8. Таким образом, для того алгоритма, который изложен далее, игра в шахматы будет не двухступенчатой, а по меньшей мере трехступенчатой системой управления. У отдельных фигур, объединенных зонами, и у фигур всего массива свои индивидуальные цели игры, но по типу общие.

Каждая фигура данного цвета стремится поразить фигуры другого цвета. Объект нападения занимает фиксированное поле массива 8*8, поразить эту мишень можно по траектории, проходящей через определенные поля доски. Раз появляется траектория, то движения фигуры становятся с точки зрения кибернетики осмысленными, появляется возможность выделять для перебора ходы, имеющие смысл, и отказаться от полного перебора ходов. Так удовлетворяется первое требование, которое было предъявлено к алгоритму.

2. Ограничение счета вариантов можно производить на принципиально иной основе. Прежде всего разъясним, в чем же состоит принципиальное различие.

Шахматная игра воспринимается шахматным мастером как неточная задача; подобные задачи люди решают непрерывно. В моей книге "Алгоритм игры в шахматы" было дано определение неточной задачи. Это такая задача, точное решение которой связано со столь большим объемом перерабатываемой информации, что устройство по переработке информации системы управления не может ее (перерабатываемую информацию) осилить. Таким образом, "точность" и "неточность" задачи определяются не только самой задачей, но и "способностями" устройства по переработке информации.

Неточная задача уже не может быть решена точно, она может быть решена лишь неточно, но как? Обычно в шахматных программах, когда цель игры определялась по Шеннону, задача решалась точно до тех пор, пока еще оставались ресурсы у ЭВМ (время и память), далее решение хирургически прерывалось, это и вызывало неточность решения.

Между тем можно еще до решения (и, видимо, это разумно) заменить задачу упрощенной моделью и это неточное отображение задачи решить более точно. В этом случае задача ограничивается не в конце перебора вариантов, а до и в процессе перебора и нежность отображения выбирается такой, чтобы решение задачи стало под силу устройству по переработке информации данной системы управления и в то же время было более высокого качества. При этом принудительного обрыва счета вариантов, как правило, нет; варианты здесь разной длины и заканчиваются сами по себе (рис. 2), когда выясняется, что уже проиграно больше материала, чем может быть выиграно.

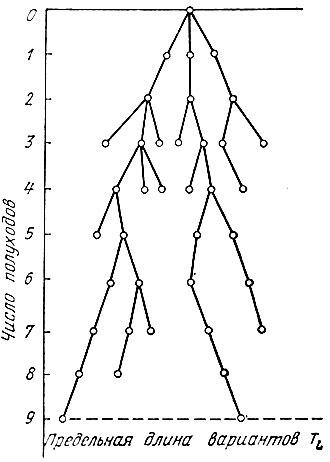
Рис. 2. Дерево перебора ходов (вариантов перебора)

Задача ограничивается горизонтом, "дальнозоркостью" (если так можно выразиться) устройства по переработке информации. Горизонт этот в процессе игры, в процессе работы системы управления может меняться - это зависит от возникающей ситуации. Если ситуация сложная, горизонт уменьшается. Устройство же по переработке информации загружено одинаковою

Таким образом, если ранее в шахматных программах задачу как бы решали точно и неточность заключалась в раннем прекращении решения, то теперь есть надежда создать неточное отображение шахматной позиции, которое может быть решено по возможности точно. И, видимо, это произойдет при удачном определении типовой цели игры.

Обрыв вариантов здесь будет принципиально иным, но в некоторых случаях, когда требуется вариант исключительно большой длины, придется ввести ограничение Длины варианта (см. рис. 2), так действует и человек.

Когда я играл в 1938 г. известную партию с Капабланкой в Роттердаме, комбинация требовала расчета оптимального варианта на 24 полухода - для меня это оказалось непосильным. Пришлось разбить оптимальный вариант на две части. Сначала я сосчитал оптимальный вариант на 12 полуходов; этот вариант можно было оборвать и пойти на него, поскольку был гарантирован ничейный исход вечным шахом. Когда же в процессе игры мы подошли к заключительной позиции первой части варианта, я сосчитал вторую часть оптимального варианта (также на 12 полуходов) и партия была закончена.

Видимо, такое же ограничение необходимо наложить и на работу программы. Это ограничение вряд ли будет фиксированным: оно должно меняться в зависимости от сложности позиции аналогично тому, как меняется предельный горизонт нападения Н_L (о чем еще будет речь далее).

Здесь уместно провести параллель между практической партией и этюдом. В практической партии возможно и реально ограничение длины вариантов, а в этюде это исключено. В сложных этюдах варианты обязательно досчитываются до конца и это возможно, поскольку решение происходит при передвижении фигур на доске; в этом случае каждая возникающая позиция рассматривается как исходная (для расчета вариантов).

Теперь уже можно в общих чертах определить основное различие между данным алгоритмом и алгоритмом, основанном лишь на сокращении длины вариантов в дереве перебора. Как уже известно читателю, и в том и в другом алгоритме варианты могут иметь ограниченную длину. Может создаться ложное впечатление, что различие между алгоритмами стирается еще и потому, что в некоторых алгоритмах, основанных на полном переборе, фактически полного перебора нет: применяются различные методы, которые позволяют исключать из дерева перебора некоторые его ветви. Это сокращенное дерево перебора соответствует не истинной позиции на доске, а какой-то условной модели позиции. Но что это за модель? Это случайная модель! Вот теперь и ясна разница между двумя типами алгоритмов: качество исходной модели для анализа.

3. Если при определении цели игры по Шеннону стандартная операция передвижения фигуры предельно примитивна (траектория передвижения фигуры в один ход), ибо передвижения фигур хаотичны, то в нашем алгоритме передвижения фигур целеустремлены, направлены к определенному полю массива 8*8, осмыслены. Стандартной операцией становится определение многоходовой траектории, длина которой соответствует дальности горизонта, т. е. сложности изучаемой позиции. Таким образом, стандартная операция передвижения фигуры усложняется - в этом существенная выгода. Итак, и здесь решающее значение имеет цель игры. При этом (как уже отмечалось ранее и как будет разъяснено далее) эти траектории получаются просто с использованием массивов 15*15.

4. Видимо, можно будет организовать работу нашей программы так, что (если это выгодно с точки зрения использования машины) пересчитывать заново уже сосчитанное не придется. Суть дела заключается в том, что математическое отображение позиции, состоящее из траекторий (точнее, пучков этих траекторий) в процессе игры меняется медленно. Из всего множества фигур в данный момент двигаться может только одна фигура; математическое отображение обладает большой инерционностью и поэтому пересчитывать надо лишь некоторую часть отображения. То же, вероятно, относится и к другим элементам информации, перерабатываемой ЭВМ по нашей программе.