Зоны игры

Получение траектории - первая осмысленная операция, которая соответствует цели игры. Следующим шагом в этом же направлении является получение зоны игры.

Цель фигуры (элементарной системы) - уничтожение неприятельской фигуры на α_k-поле траектории нападения. В процессе передвижения атакующей фигуры к своей мишени неприятельские фигуры противодействуют нападению, свои - поддерживают. (Здесь уже руководит ими не своя цель игры; они подчиняются решению совокупности элементарных систем, решению, соответствующему цели игры этой совокупности). Все они действуют по своим траекториям. Таким образом, часть фигур, находящихся на доске, по своим траекториям участвует в этом местном бою. Все эти фигуры и траектории их передвижения составляют зону нападения. Будем называть траекторию α₀-фигуры комлевой траекторией зоны.

Зону можно также рассматривать как два противоборствующих лагеря фигур; совокупность всех противоборствующих фигур на доске, участвующих в игре, можно считать совокупностью зон.

Структура зоны детерминирована. Фигуры, принадлежащие к тому же лагерю, что атакующая, будем обозначать знаком (+), фигуры того лагеря, к которому принадлежит атакованная,- знаком (-). Эти же обозначения^* распространяются на так называемую связанную зону (о чем речь будет далее). Но там атакующая фигура (+) атакует не неприятельскую фигуру, а определенное поле доски; фигуры (-) противодействуют этой атаке. Фигуры (+) и (-) не белые и черные фигуры. И белые и черные фигуры могут быть одновременно фигурами и (+), и (-), но в разных простых зонах. В дальнейшем будет введено понятие сложной зоны, являющейся объединением простых. В такой зоне фигуры одного цвета могут быть и (+) и (-).

Принято, что поскольку комлевая фигура (+) атакует, в зоне игры из всех фигур (+) может двигаться только одна комлевая фигура: она пробивается к цели. Другие фигуры (+) имеют право двигаться лишь тогда, когда они в процессе игры в зоне могут непосредственно уничтожать неприятельские фигуры (+). Отсюда ясно, что фигуры (+), которые контролируют поля какой-либо траектории в зоне, должны находиться в засаде на расстоянии одного передвижения от этого поля. Только в этом случае контролирующая фигура (+) может быть включена в зону игры.

^* (Знак (+) будем читать как "плюс"; знак (-) - как "минус")

Еще более строг отбор фигур (+) для участия в блокаде. Блокирующая фигура (+) участвует в зоне игры лишь тогда, когда она уже блокирует данное поле траектории, т. е. можно сказать, что число передвижений, приводящих к возникновению блокады, в траектории блокады равно нулю.

Фигуры (-) могут передвигаться в зоне без подобных ограничений, да это и понятно. Если цель фигур (+) в зоне состоит в том, чтобы пробиться к цели, и поэтому перемещается лишь комлевая фигура, то цель фигур (-) состоит в противодействии, а оно может быть реализовано с помощью передвижений любой фигуры (-), поэтому и может двигаться любая фигура (-), включенная в зону.

Атакованная фигура (-) может, конечно, и отступать. Для упрощения задачи принято, что траектория отступления состоит из одного передвижения. Принято также, что траектория деблокады поля тоже состоит лишь из одного передвижения. Деблокада любой фигурой, как и отступление, составляет отдельную связанную зону.

Вообще, можно принять, что в алгоритме есть только два действия фигур: нападение и отступление. Под нападением следует понимать как собственно нападение, так и контроль (в этом случае атакуется α-поле, но подразумевается, что на этом поле как бы находится или будет находиться фигура), а также блокада. Правда, может блокироваться и |3-поле, где формально фигуры нет, но если принять, что дальнобойная фигура, перемещаясь от α_i-поля к α_i+1-полю, последовательно занимает все β-поля между этими α-полями, то и блокада всегда сводится к нападению. Под отступлением следует понимать как собственно отступление, так и деблокаду. Такая формализация облегчает работу над программой формирования зоны игры.

Теперь для иллюстрации рассмотрим нулевую зону Игры, изображенную на рис. 6; эта зона нападения обведена жирным пунктиром. Фигура ( + , 0.0) является комлевой: она находится в комле нулевой траектории нападения. Первый нуль означает, что фигура эта принадлежит нулевой зоне (зоне нападения), второй нуль - что фигура принадлежит нулевой траектории. Стрелками указаны направления движения фигур по траекториям.

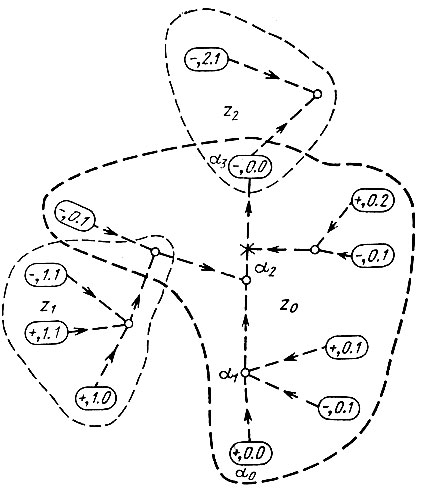
Рис. 6. Нулевая зона и две связанные

В данном случае траектория нападения состоит из трех передвижений. На конечном α_k-поле (в данном случае это аз-поле) находится атакованная фигура (-, 0.0). Первый и второй нули говорят о принадлежности этой фигуры к нулевой траектории нулевой зоны.

Все остальные траектории, концы которых связаны с полями нулевой траектории, являются траекториями первого отрицания.

Траектории фигур (-, 0.1) и ( + , 0.1), контролирующих "i-поле нулевой траектории,- траектории первого отрицания, о чем и свидетельствует единица; Это же относится и к фигуре (-, 0.1), связанной с α₃-полем нулевой траектории; траектория контроля этой фигуры состоит из двух передвижений. Наконец, есть фигура (-, 0.1), которая стремится блокировать β-поле (между α₂- и α₃-полями нулевой траектории), обозначенное крестиком; эта фигура действует по траектории первого отрицания. А вот фигура ( + , 0.2), контролирующая α_i-поле этой последней траектории блокады, действует уже по траектории второго отрицания.

О горизонте для траектории нападения было уже сказано вполне достаточно, особо остановимся на горизонте траекторий первого (и выше) отрицания. Прежде всего, число передвижений здесь зависит от очереди хода. Дело в том, что горизонт нападения выгодно выбрать четным (2 полухода, 4 полухода и т. д.); в этом случае число передвижений в траектории не зависит от очереди хода, как это следует из формулы, определяющей число передвижений:

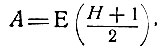
где E(z) - целая часть числа z.

Например, при Н = 6 или H = 5 предельное число передвижений всегда равно трем; стало быть, если при ходе стороны (+) задать H = 6, то, хотя при перемене очереди хода сторона (+) будет иметь лишь 5 полуходов, траектория нападения в три передвижения остается в пределах "видимости". Что же касается горизонта траекторий отрицания, то на все траектории отрицания стороны (-), связаные с данным полем траектории нападения, дается определенное число полуходов, зависящее от индекса этого поля траектории нападения. Если исходить из числа полуходов H₀, необходимых на перемещение атакующей фигуры до конца траектории нападения, и номера поля i, то на контроль α_i-поля или на блокаду β-поля (i - номер α-поля, a j - номер β-поля из числа β-полей, следующих непосредственно за α_i-полем), можно затратить не более Н_х полуходов:

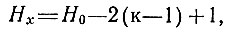
где к - номер конечного α_k-поля нулевой траектории.

Это количество полуходов Н_х отводится не только на передвижение фигуры (-) по траектории первого отрицания, но, как уже отмечалось, и на передвижения всех отрицающих фигур (-), связанных с контролем (блоками) данного α-поля (β-поля) нулевой траектории. Поэтому после подсчета величины Н_х следует вести учет расходования полуходов для того, чтобы можно было всегда вычислить предельное число передвижений для какой-то следующей промежуточной траектории.

Из формулы, определяющей Н_х, следует, что Н_х всегда нечетно при четном Н₀. В этом случае число передвижений зависит от очереди хода. Поэтому предельное число передвижений в траекториях отрицания меняется и зона как бы "дышит": часть отрицающих фигур то входит в зону игры, то уходит из зоны. Проще всего сказать, что есть два пограничных значения зоны, соответствующих очереди хода той и другой стороны. Нулевая зона, представленная на рис. 6, составлена для очереди хода стороны (+).

Представим себе, что размен на α₁-поле в пользу стороны (+), блокада β-поля (за α₂-полем) невозможна (это очевидно), отступление также исключено, ибо поле, куда фигура может отступить, контролируется фигурой (+). Но атакующая фигура (+) не может пробиться к цели, так как α₂-поле контролируется фигурой (-). Ситуация в зоне может быть улучшена для стороны (+) лишь при условии подведения в зону других фигур (+): вот мы и подошли к необходимости составления связанной зоны контроля. К этому еще вернемся, а сейчас отметим лишь, что программа должна начать поиск фигур, которые могут изменить положение на полях траектории первого отрицания, контролирующей α₂-поле траектории нападения.

Примем, что такая фигура найдена: это фигура (+ , 1.0), которая становится комлевой фигурой связанной зоны (зоны первой степени). Мишенью этой комлевой фигуры (+) является уже не фигура (-), а α₁-поле траектории первого отрицания. Таким образом, комлевая фигура связанной зоны так же, как отрицающие фигуры, подчиняется уже не своей цели, а цели игры совокупности играющих в зоне фигур.

В данной сложной зоне исход борьбы зависит только от результата размена на α₁-поле нулевой траектории связанной зоны. Если размен в пользу стороны (+), то комлевая фигура может занять это α₁-поле и осуществить контроль над α₁-полем траектории отрицания нулевой зоны. Тогда эта комлевая фигура (+) войдет в нулевую зону как фигура (+), действующая по траектории второго отрицания нулевой зоны. Ситуация в зоне изменится, и выигрыш материала стороной (+) обеспечен.

Здесь мы имели сложную зону, объединяющую нулевую зону и связанные. Возможны сложные зоны и другого типа. Если, например, комлевая фигура нулевой зоны сама является объектом нападения, атакованной фигурой в другой нулевой зоне, то эти две нулевые зоны также образуют сложную зону.

В рассмотренных зонах каждая фигура имела лишь одно действие, одну траекторию. Фактически бывает и иначе. Совокупность зон образует математическое отображение шахматной позиции (МО).

С помощью зон можно реализовать одно из основных требований, предъявляемых к алгоритму,-не пересчитывать уже сосчитанного. Суть дела в том, что всегда есть зоны (сложную зону также будем называть зоной), которые не зависят друг от друга. Когда по каким-либо причинам зона меняется, это не означает, что меняются все зоны игры; наоборот, это означает, что в какой-то части МО зоны остаются неизменными, а, стало быть, там и пересчитывать нечего. Реализация этого принципа, когда это выгодно, дает возможность программисту сделать работу машины производительней.

Фигуры и их траектории еще не являются элементами МО, это только материал, из которого МО строится. Зоны - это уже составные элементы МО.

Итак, мы убедились, что наш алгоритм удовлетворяет четырем принципам составления алгоритма: выделению информации первостепенной важности, ограничению счета вариантов перебора (хотя это еще подлежит дальнейшему рассмотрению), стандартизации возможно более сложных повторяющихся операций и тому, чтобы не пересчитывать уже сосчитанного.