Стандартная операция определения траектории

Так как на свободной от фигур доске траектория (или, точнее, пучок траекторий) передвижения фигуры данного типа от заданного начального поля до другого заданного поля никогда не меняется, то определение такой траектории -операция не оригинальная, а стандартная. В этом и состоит возможность простого решения задачи.

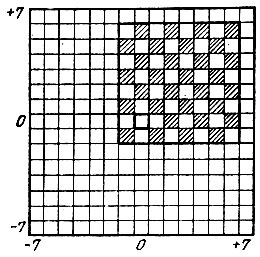
Рис. 3. Совмещение двух массивов

Препятствием для решения является то, что исходное поле, с которого фигура может начать движение, имеет 64 значения. Напрашивается такой путь: иметь дело не с массивом 8*8 (доской) для запоминания всех возможных траекторий, а с каким-то другим массивом, где исходное поле фиксировано. Тогда, совмещая массив 8*8 с новым массивом так, чтобы начальное поле траектории в массиве 8*8 совпадало с упомянутым фиксированным полем нового массива, можно передать необходимую информацию с полей нового массива на поля массива 8*8. Нетрудно понять, что таким новым массивом должен быть массив 15*15, а фиксированным полем, с которым совмещается начальное поле траектории передвижения, должно быть центральное поле массива 15*15. Именно при этих размерах нового массива всегда возможно наложение массива 8*8 на массив 15*15 (при совпадении его центрального поля с начальным полем траектории). При меньших размерах часть массива 8*8 могла бы выходить за пределы нового массива, а при больших - появилась бы избыточная информация, так как часть плоскости массива, выходящая за размеры 15*15, никогда бы не использовалась. Это становится ясным при рассмотрении примерного совмещения массивов 8*8 и 15*15, изображенного на рис. 3.

Рис. 4. Массив 15*15 для коня

Массивы 15*15 для различных фигур составляются аналогично, поэтому достаточно рассмотреть два типичных массива: для фигур, перемещающихся в одно передвижение на фиксированное расстояние (конь и, как правило, король, и пешка), и для фигур, перемещающихся в одно передвижение на разные расстояния (ферзь, ладья и слон). Поля, на которых фигура останавливается, будем называть α-полями, поля, которые фигура проходит без остановки - β-полями. У фигур, перемещающихся на фиксированное расстояние, β-полей нет (кроме пешки, когда с начальной позиции она перемещается на два поля, и короля, когда он совершает рокировку). Массивы 15*15 для коня и ладьи изображены на рис. 4 и 5 соответственно.

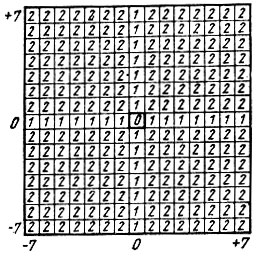
Рис. 5. Массив 15*15 для ладьи

На центральном поле массива фигура занимает исходную позицию. Любое другое поле массива может быть конечным полем траектории перемещения фигуры. Числа, расположенные на полях массива, равны минимальному числу ходов, необходимых для перемещения фигур по кратчайшим траекториям.

Совмещение массивов 15*15 и 8*8 эквивалентно элементарному пересчету координат. Цель совмещения состоит в том, чтобы число с поля массива 15*15, с поля, имеющего в этом массиве заданные координаты, передать полю массива 8*8, также имеющему в массиве 8*8 заданные координаты. Разность между координатами центрального поля массива 15*15 и координатами поля, содержащего передаваемое число, всегда равна разности между координатами начального поля траектории и поля, которому число передается (в массиве 8*8). Поэтому, пересчитав координаты полей массива 8*8 на координаты массива 15*15, можно легко найти искомое передаваемое число. Когда нужно передать одно или несколько чисел, операцию совмещения (передачи и запоминания всех 63 чисел) вряд ли следует производить, так как это связано с непроизводительным трудом и расходом машинного времени. Как будет ясно из дальнейшего, получение любой траектории, в основам, связано с операцией совмещения массивов, производимой в различных комбинациях.

Цель игры была уже определена ранее, сейчас объясним способ выделения информации первостепенной важности (получение траектории). Но как быть с ограничением задачи - ограничением счета числа вариантов? Ограничение задачи, как это будет рассмотрено далее, прежде всего производится по методу горизонта, по количеству полуходов, которые должны быть затрачены на передвижение фигуры по траектории нападения на свободной от фигур доске. Чем меньше горизонт, чем короче траектории нападения, тем сильнее ограничение задачи. Итак, горизонт (будем обозначать его буквой Н_L задается в полуходах.

Поскольку одному и тому же горизонту H_L могут соответствовать предельные траектории разного числа передвижений (число а-полей при том же горизонте может отличиться на единицу, все зависит от очереди хода), то прежде всего надо определить число передвижений А, соответствующее заданному горизонту H_L. Эта элементарная операция, не требующая каких-либо пояснений. Теперь можно приступить к поиску траектории, поскольку число передвижений уже известно.

Прежде всего, необходима процедура, которая состоит в совмещении массивов 15*15 и 8*8 (при этом выбирается массив 15*15, принадлежащий той фигуре, траектория передвижения которой определяется) таким образом, что начальное α₀-поле траектории массива 8*8 совмещается с центральным полем. Операция совмещения по сути дела состоит в том, что отмечаются все координаты полей массива 8*8, на которые соответственно переходят числа 1, 2, ..., А-1, А. Массив 8*8, у которого α₀-поле совпадает с центральным полем массива 15*15, будем обозначать 8*8α₀. Когда же у этого массива искомые координаты полей уже определены, возьмем это обозначение в скобки: (8*8α₀). Этих же обозначений будем придерживаться во всех аналогичных случаях.

Далее, следует убедиться в том, что такая траектория в условиях данного алгоритма действительно существует. Идет поиск не вообще траектории, а конкретной траектории от α₀-поля до α_k-поля, от начального до конечного поля возможной траектории. Если n>A (n - число, которое должно быть передано α_k-полю массива 8*8 от соответствующего поля массива 15*15), то в пределах заданного горизонта H_L траектории, очевидно, нет. Однако может быть и другой случай, когда n<A, а траектории (по данному алгоритму) также нет.

Суть дела в том, что для дальнобойных фигур в массивах 15*15 не содержится чисел более двух. Как известно, дальнобойными фигурами является ферзь, ладья и слон. В массиве 15*15 для ферзя даже число два встречается редко, поэтому надлежит вообще отказаться от специального массива 15*15 для ферзя, а пользоваться для нахождения траектории передвижения ферзя массивами 15*15 для ладьи и слона: там число два встречается чаще. Но даже и при введении этой тонкости нет возможности определить кратчайшую траекторию передвижения дальнобойной фугуры, скажем, в три передвижения.

Эти же трудности возникают и при определении некратчайшей траектории как для дальнобойной, так и для недальнобойной фигуры (короля и коня). Очевидно, что, когда речь идет о траектории передвижения дальнобойной фигуры в три передвижения, также подразумевается получение некратчайшей траектории. Когда мы говорим "некратчайшая" траектория, то имеем в виду некратчайшую траекторию на свободной от фигур доске. На заставленной фигурами доске эта траектория может быть уже кратчайшей. Поэтому ЭВМ должна уметь находить некратчайшие траектории.

Так как способ совмещения массивов 15*15 и 8*8 приводит лишь к определению кратчайших траекторий на свободной от фигур доске, то неизбежно приходится обратиться к поиску стыкованных траекторий, состоящих из ряда кратчайших. Чтобы не усложнять чрезмерно программу, ограничим число кратчайших траекторий, образующих стыкованную траекторию. Принято, что стыкованные траектории могут быть образованы лишь из двух кратчайших. Тогда, если ввести обозначение n_L - наибольшее число, содержащееся в массиве 15*15, то для дальнобойных фигур стыкованная траектория может состоять не более как из четырех передвижений, а вообще говоря, из 2n_L передвижений. Однако ничего особо плохого в этом нет. У дальнобойных фигур траектории более ограничены, нежели у недальнобойных, но в этом есть свой смысл: действия фигур будут более координированы (пехота поспевает за танками).

Определить стыкованную траекторию, составленную из двух кратчайших, нетрудно.

Теперь можно понять, почему иногда при n>A траектории все же нет: это происходит, когда 2n_L<A. Стало быть, траекторию по данному алгоритму можно найти только в том случае, если n≤A≤2n_L. Если это условие не выполняется, траектории нет, если выполняется, работа по поиску траектории продолжается. Тогда происходит операция совмещения, полностью аналогичная приведенной ранее; различие состоит лишь в том, что с центральным полем массива 15*15 совмещается не α₀-поле траектории в массиве 8*8, а α_k-поле.

В массиве (8*8α₀) и массиве (8*8α_k) мы имеем отобранные поля (координаты полей) с соответствующими числами. Там, где на соответствующих полях (с одинаковыми координатами) сумма чисел равна n, и находятся α-поля искомой траектории (точнее, пучка искомых траекторий).

Теперь надо проверить, какого типа траектория подлежит поиску: кратчайшая или стыкованная из двух кратчайших. Если n = А, надлежит искать кратчайшую траекторию, что сравнительно легко; если n<A≤2n_L, траектория должна быть стыкованной. На этом закончим пояснение способа получения траекторий (более подробно метод изложен в приложении 1).

Итак, можно подвести некоторые итоги. Стандартная операция получения траектории передвижения фигуры по данному алгоритму (когда правильно определена паллиативная цель неточной игры) реализуется относительно простым методом. Эта операция формализуема, т. е. может быть запрограммирована. Когда получение любой траектории оказывается результатом работы подпрограммы, это означает, что ЭВМ может уже не заниматься непроизводительным перебором возможностей, лишенных смысла. ЭВМ "понимает", в каком направлении надо передвигать фигуры для реализации цели игры. Это первый робкий шаг на пути создания искусственного интеллекта, робкий, но может быть самый трудный: решена задача как выделения информации первостепенной важности, так и стандартизации сложной операции получения траектории.