Независимые зоны

Независимая зона (в том смысле, что она не зависит от других зон: в одном варианте перебора нет общих фигур и полей с другими зонами) может быть простой нулевой, сложной нулевой со связанными зонами и, наконец, сложной зоной, состоящей из нескольких нулевых зон, имеющих в общем случае и связанные зоны.

Перебор в независимой зоне казалось бы не связан с переборами в других независимых зонах, так как у этих зон нет общих фигур и полей, но эти переборы могут быть связаны распределением избыточного времени, если оно есть в каких-либо независимых зонах. К определению понятия избыточного времени мы еще вернемся.

Практическая независимость переборов в независимых зонах предопределяет ограничение перебора в целом, ибо варианты ходов резко сокращаются. Сокращаются они еще и потому, что в большинстве независимых зон оптимальный вариант перебора состоит в том, что фигуры должны оставаться на своих местах.

Будем рассматривать наиболее сложную независимую зону, составленную из множества простых нулевых и связанных зон, причем эти зоны содержат как белые, так и черные α₀-фигуры. Следует определить, до каких пор продолжать вариант перебора? Обрыв варианта в каждой простой зоне, входящей в сложную, может происходить, если α₀-фигура уничтожена или заблокирована так, что снятие блокады невозможно, и если α_л-фигура уничтожена или отступила на безопасное поле.

При выполнении одного из условий игра в этой простой зоне должна быть прекращена, что, однако, не означает прекращения игры в других простых зонах. Наоборот, игра в других зонах (простых) должна продолжаться, т. е. игра в той сложной зоне, которую мы рассматриваем, должна продолжаться до тех пор, пока не будет выполнено еще одно условие, определяющее прекращение перебора уже во всей сложной зоне. Прежде всего рассмотрим действие этого условия в независимой простой зоне, т. е. сведем наиболее сложный случай к наиболее простому. Каково тогда будет третье условие обрыва варианта?

Ранее автором был сформулирован следующий принцип: то, что потеряно, должно быть меньше того, что может быть выиграно. Это положение было названо "формулой надежды". Однако этот принцип должен быть расширен, поскольку справедливо и иное положение: можно что-то терять в надежде, что в будущем благодаря этому будет потеряно меньше. Смысл принципа заключается в том, что всегда лучше потерять сейчас меньше, чем в дальнейшем больше! Это означает, что не следует обрывать вариант, когда сторона (-) потеряла материал меньший, чем m_k, ибо возможно, что это спасет α_k-фигуру.

Итак, формулу надежды можно записать в следующем виде:

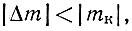
где Δm - материал, потерянный любой стороной, а m_k - стоимость (α_k-фигуры. Это формула относится к простой независимой зоне.

В сложной независимой зоне может быть уже не одна α_k-фигура, а несколько таких фигур, и они могут быть разного цвета. Таким образом, вместо m_k мы имеем ∑m_{k b} и ∑m_{k ω}, где m_{k b} - стоимость черных α_k-фигур, a m_{k ω} - стоимость белых α_k-фигур. Как же определить допустимую величину потерянного материала в сложной зоне, когда вариант перебора еще нужно продолжать?

Ясно, что если материал, потерянный белыми в своих простых зонах, меньше |∑m_{k b}|, то вариант продолжать надо. А если белые потеряли при этом материал и в "черных" зонах, что тогда? Очевидно, если этот потерянный материал меньше |∑m_{k ω}|, вариант также нужно продолжать. Следовательно, если

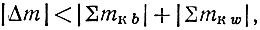
то вариант перебора продолжается. Эта формула действует и для белых и для черных. Формула превращается в предыдущую, если сложная зона превращается в простую. Следует иметь в виду, что ∑m_k может меняться от хода к ходу.

Таким образом, при переборе в сложной независимой зоне должен вестись двойной учет. Первые два условия определяют прекращение варианта перебора в каждой простой зоне. Третье условие обрывает вариант перебора во всей сложной независимой зоне.