Вычислительные машины. Аналоговые вычислительные устройства
Для обработки геолого-геофизической информации применяются в основном вычислительные машины двух классов - аналоговые вычислительные устройства (АВУ) и электронные цифровые вычислительные машины (ЭЦВМ)1.
1 (Для названия вычислительных машин используют различные сокращения - БЭЦМ, ЦАМ, ЭВМ и др. Мы применяем сокращения, используемые в реферативных журналах "Математика", "Научно-техническая информация" и др.)
Аналоговые устройства (устройства непрерывного действия). Аналоговыми называется широкий круг счетно-решающих и моделирующих устройств. В устройствах этого класса входные величины ("условия задачи") задаются, как правило, в непрерывной форме, например, в виде электрического напряжения, снимаемого с некоторой части реостата. В непрерывной же форме (в этом их основное отличие от цифровых машин) происходит и преобразование этих величин в процессе решения задачи. Выходные величины также чаще всего выдаются в непрерывной форме - в виде графиков или показаний прибора для визуального отсчета.
Провести четкую границу между обычными моделями и аналоговыми вычислительными устройствами довольно сложно.
Можно выделить три вида моделирования: а) непосредственное; б) с учетом критериев подобия; в) на принципе аналогий.
Непосредственное моделирование заключается в том, что в лабораторных условиях создают модели, параметры которых соответствуют естественным условиям. Так, для изучения распределения нейтронов в горных породах в условиях скважины создаются модели из блоков известняка или песчаника так, чтобы физические свойства этих пород (в частности, пористость) и геометрия модели соответствовали реальным пластам, пересеченным скважиной.
Воссоздать в лаборатории модели, точно соответствующие реальным условиям, часто бывает трудно или же просто невозможно. В связи с этим возникает необходимость изменить некоторые параметры модели, например, ее геометрические размеры. Однако изменение численных значений одних параметров модели очень часто влечет за собой необходимость изменения других. Каков характер этого изменения, изучает теория подобия. Так, если в упомянутом выше примере моделирования распределения нейтронов в горных породах изменить геометрические размеры модели, то оказывается необходимым изменить плотность всех сред - пласта, бурового раствора, обсадных труб, скважинного снаряда и др. Наоборот, если мы желаем изменить плотность сред, то должны изменить и размеры модели.
Связь между параметрами модели задается так называемыми "критериями подобия", величина которых при подобных преобразованиях модели должна оставаться постоянной.
Так, в рассматриваемом случае моделирования задач нейтронной разведки критерием подобия служит величина
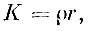
где r - линейный размер; ρ - плотность.
Таким образом, уменьшая плотность сред в n раз, чтобы удовлетворить требованию постоянства величины критерия подобия, мы должны в n раз увеличить размеры модели1.
1 (Методика моделирования задач нейтронной разведки на основе принципа подобия разработана Ш. А. Губерманом [18].)
Учет критериев подобия важен при моделировании, связанном с решением различных задач как в области поисков и разведки полезных ископаемых, так и в теоретической геологии. Например, при моделировании тектонических процессов, протекающих в земной коре (при решении задач тектонофизики), изменение геометрических размеров модели влечет за собой изменение вязкости пластов.
При моделировании индукционных методов электроразведки необходимо учитывать критерий подобия:
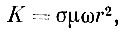
где σ - удельная электрическая проводимость; μ - магнитная проницаемость; ω - частота тока; r - линейный размер.
Уменьшение размеров модели в n раз требует увеличения частоты тока питания в n2 раз или же уменьшения удельного сопротивления в n2 раз1.
1 (Моделирование задач индукционной разведки разработано проф. Л. М. Альпиным [3]. В частности, им предложен "кольцевой индукционный интегратор" - аналоговое устройство, предназначенное для решения задач теории индукционного каротажа.)
Вывод критериев подобия производится на основе анализа уравнений (как правило, дифференциальных или же интегродифференциальных), описывающих распределение исследуемых величин.
Уравнения, относящиеся к различным физическим процессам и явлениям, часто оказываются одинаковыми. Это позволяет для изучения одних величин использовать модели совершенно другой физической природы. Например, распределение электрического тока описывается теми же дифференциальными уравнениями, что и распределение грунтовых вод. В соответствии с этим для решения гидрогеологических задач (т. е. для интегрирования соответствующих дифференциальных уравнений) можно воспользоваться моделированием в электролитической ванне. По распределению потенциала в этой ванне можно сделать заключение о распределении вектора скорости грунтовых вод. Вместо электролитической ванны часто бывает более удобным использовать сетку из электрических сопротивлений. Такие моделирующие устройства для решения гидрогеологических задач на основе электрического моделирования называются интеграторами ЭГДА (электро-гидродинамическая аналогия).
Электрическое моделирование может быть применено на основе принципа аналогии для решения самых различных задач, в частности, уже упоминавшихся выше задач нейтронной разведки [32] и тектонофизики. Принцип аналогии используется в устройствах, связанных с решением самых разнообразных задач, и именно поэтому устройства непрерывного действия получили название "аналоговых". Эти устройства могут и не быть моделирующими. Так, пантографы, с помощью которых осуществляется перевод карт из одного масштаба в другой, планиметры для вычисления площадей на чертеже, наконец, логарифмическая линейка и многие другие устройства из обихода разведочных партий принадлежат к устройствам аналогового типа.
Ряд аналоговых машин представляет собой совокупность счетно-решающих звеньев, причем каждое такое звено выполняет определенную операцию - сложения, вычитания, умножения, деления, дифференцирования, интегрирования и т. п. Звенья могут быть различной природы - механические, электрические, гидравлические, пневматические и др. Наиболее распространены электрические и механические звенья.
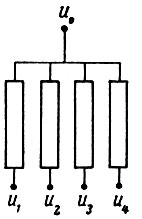
Рис. 2. Простейшее вычислительное звено АВУ.
Одно из простейших электрических суммирующих звеньев приведено на рис. 2.
Значения потенциалов в точках U1, U2, U3, ..., Un являются входными параметрами, значение потенциала в точке U0 - выходной параметр. Согласно первому закону Кирхгофа, алгебраическая сумма токов, втекающих в узел, равна нулю. Следовательно, если пренебречь током, протекающим через гальванометр, то
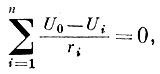 (1)
(1)где ri - величина i-того электрического сопротивления.
После элементарных преобразований из (1) получаем:
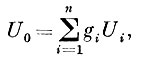 (2)
(2)где
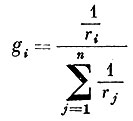
доля проводимости, соответствующая i-тому сопротивлению, в общей проводимости сопротивлений r1, r2,..., rn.
Таким образом, счетно-решающее звено, показанное на рис. 2, реализует суммирование величин U1, U2, ..., Un с некоторым "весом" (т. е. суммирование, сопровождающееся предварительным умножением на некоторый коэффициент gi).
Пример счетно-решающего устройства, использующего такое звено, будет рассмотрен ниже.
В качестве множительного звена может фигурировать трансформатор, радиотехнический усилитель и др.
Из крупных аналоговых машин, используемых для решения геологоразведочных задач, могут быть упомянуты электроинтеграторы ЭКСМ, ПЭГ, ЭИ-С.
Электроинтегратор ЭКСМ (электрокаротажная сетчатая модель) представляет собой специализированное моделирующее устройство, предназначенное для получения теоретических кривых электрического каротажа [1, 33]. Он занимает площадь 30-40 м2. Электроинтегратор содержит 62 тыс. электрических сопротивлений. Основная часть модели - сетка из электрических сопротивлений - разбита на блоки, и каждый из этих блоков моделирует определенный участок столба бурового раствора или окружающих пластов. Имеются блоки пластов, соответствующие различным удельным сопротивлениям. Подключая соответствующим образом эти блоки, можно собрать модель произвольного разреза, в частности, разреза, представленного частым переслаиванием тонких пластов. Интегратор располагает автоматическим устройством, осуществляющим переключения, соответствующие перемещению зонда вдоль ствола скважины. С помощью самописца теоретическая кривая кажущегося сопротивления записывается на бумажной ленте. Время решения одной задачи (определения одного значения кажущегося сопротивления) около 1 сек. Точность решения - 1% от измеряемой величины.
В электроинтеграторе ЭКСМ используется плоская сетка, вследствие чего можно моделировать только те задачи, которые характеризуются цилиндрически-симметричным распределением электрического поля.
Эти условия, например, соблюдаются в случаях, когда пласт перпендикулярен скважине, а источник тока находится на оси скважины. Если же источник тока (точечный) находится у стенки скважины (случай каротажа микрозондами) или же пласты наклонены по отношению к скважине, то использование ЭКСМ для решения задач не представляется возможным.
Созданный Л. Б. Ницецким, А. Ф. Фокиным и Ю. А. Мендельсоном [48] электроинтегратор ПЭГ (пространственный электроинтегратор геофизический") располагает уже не плоской (двумерной), а пространственной (трехмерной) сеткой и предназначен для решения задач электро-, грави- и магниторазведки.
Электроинтегратор ЭИ-С [50] с сеткой из электрических сопротивлений и конденсаторов позволяет решать различные нестационарные задачи, связанные с эксплуатацией нефтяных месторождений. Площадь, занимаемая интегратором, 200 м2, потребление электроэнергии 60 кв, численность обслуживающего персонала 6-8 человек.
Экономическую эффективность этого уникального интегратора можно проиллюстрировать следующим примером. В результате моделирования на ЭИ-С различных вариантов разработки одного из нефтяных месторождений Татарской АССР был найден и рекомендован вариант эксплуатации, позволивший, с одной стороны, сократить число эксплуатационных скважин, а с другой - увеличить количество отбираемой нефти на 5-7%.
Стоимость больших интеграторов (ПЭГ, ЭКСМ, ЭИ-С) составляет от нескольких десятков до нескольких сотен тысяч рублей.
В качестве примера малых моделей можно привести электролитические модели с неискажающими стенками, предложенные Л. М. Альпиным [2]. В этих моделях поверхности раздела сред с различными удельными электрическими сопротивлениями выполняются в виде листов изолятора, перфорированного по сетке проводником (медью). Такие перегородки, не искажая существенно электрического поля, препятствуют смешению электролита.
Л. Б. Ницецким и А. Ф. Фокиным предложена портативная установка для моделирования двумерных задач геофизики [49]. Модели на проводящей бумаге использовались для решения различных задач электроразведки.
Для решения гидрогеологических задач (расчеты установившегося и неустановившегося движения вод) применяются электроинтеграторы сеточного типа ЭИ-12, электроинтеграторы ЭГДА 9/60, ЭГДА-10, ИПП-11, гидроинтегратор ИГЛ.
Аналоговые вычислительные устройства обладают рядом важных качеств: простотой в эксплуатации, портативностью и сравнительно невысокой стоимостью большинства машин этого класса, быстротой получения ответа, благодаря чему эти устройства получили весьма широкое распространение. К недостаткам АВУ следует отнести сравнительно невысокую точность решения и их резко специализированный характер - каждое устройство, как правило, предназначается для решения весьма узкого круга задач. А так как число задач, связанных с проблемами поисков и разведки полезных ископаемых, исключительно велико, то при желании ограничиться вычислительными устройствами только этого класса пришлось бы ставить вопрос о создании внушительного арсенала вычислительных машин.
Малая "гибкость" аналоговых машин обусловлена тем, что "программа" в них реализуется соединением электронных (или электрических, механических и др.) узлов, набор которых не может быть неограниченным в силу соображений стоимости и габаритов.
Специализированный характер АВУ определенным образом сдерживает создание больших машин этого класса, так как для решения сравнительно узкого круга задач необходимо создание машин, требующих больших капиталовложений. Однако в тех случаях, когда задачи, пусть весьма специализированные, имеют массовый характер (например, при разработке теории электрического каротажа стоит вопрос о получении многих тысяч, а возможно, и десятков тысяч кривых), создание больших АВУ вполне оправдывает себя.
Целесообразность применения аналоговых вычислительных машин обусловлена тем, что они являются в определенном смысле более быстродействующими, чем цифровые. При моделировании на аналоговых машинах процессы могут протекать в очень малые промежутки времени вплоть до долей секунд. Математически же эти процессы представлены уравнениями, решение которых может требовать многих тысяч, миллионов и даже миллиардов операций, в результате чего цифровая вычислительная машина, даже самая быстродействующая, затратит на решение во много раз больше времени, чем АВУ.
Использование аналоговых устройств, особенно моделирующих, при решений различных задач, связанных с поисками и разведкой полезных ископаемых, имеет давнюю традицию. Однако это использование носило скорее случайный, чем планомерный характер и до последнего времени касалось почти исключительно вопросов разработки теории исследований, т. е. решения "прямых" задач разведки. В последние годы аналоговые устройства получили применение и для решения обратных задач разведки, т. е. для обработки результатов полевых (пока в основном геофизических) наблюдений.
Очень простым устройством такого рода является интегратор Клушина-Никольского для обработки гравитационных карт [26]. Как известно, одной из важных задач интерпретации данных гравиметровой съемки является разделение гравитационного поля на региональную и локальную составляющие. Это разделение осуществляется путём осреднения замеренных значений гравитационного поля по формуле
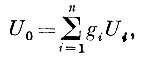 (3)
(3)которая совпадает с формулой (2), вследствие чего для вычисления U0 можно воспользоваться суммирующим звеном, показанным на рис. 21.
1 (Выражение (3) получается путем приведения к форме для численного расчета интегральной формулы
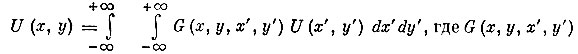
ядро преобразования, вид которого определяется характером преобразования (перерасчет с одной высоты на другую; вычисление первой, второй производной, осреднение, фильтрация ошибок наблюдения и т. д.).)
Счетно-решающее устройство представляет собой контактное ("наборное") поле, на контакты которого с делителя напряжения подаются электрические потенциалы, численно равные значениям трансформируемого поля в соответствующих точках. Подключая к контактам наборного поля суммирующее звено (И. Г. Клушин и Ю. И. Никольский называют его "электрической палеткой"), мы получим значение поля после трансформации. Переходя от точки к точке, получим преобразованное поле на всем планшете (за исключением краевых участков).
Схема интегратора Клушина-Никольского приведена на рис. 3.
![Рис. 3. Принципиальная схема интегратора Клушина-Никольского [27]. А - наборное поле; Б - 'палетка' (суммирующее звено); В - делитель напряжения; Г - блок питания (стабилизатор и выпрямитель)](pic/000010.jpg)
Рис. 3. Принципиальная схема интегратора Клушина-Никольского [27]. А - наборное поле; Б - 'палетка' (суммирующее звено); В - делитель напряжения; Г - блок питания (стабилизатор и выпрямитель)
Широкое применение (особенно за рубежом) получили аналоговые устройства для преобразования сейсмограмм во временные разрезы. Простейшим способом преобразования сейсмограмм во временные разрезы является соответствующая компоновка (склеивание) их мелкомасштабных дубликатов [73]. Более совершенное преобразование сейсмограмм в разрез предусматривает внесение ряда поправок во времена - за рельеф, за зону малых скоростей, за геометрическое размещение пунктов взрыва и сейсмоприемников. Внедрение магнитной записи позволило автоматизировать процесс внесения указанных поправок на основе применения специальных аналоговых устройств. В настоящее время как в СССР, так и за рубежом предложено большое число таких устройств, имеющих в своей основе один и тот же принцип работы, реализуемый различными средствами. Отличия наблюдаются в функциональных узлах: конструкциях воспроизводящих узлов, методах введения поправок, способах представления временных разрезов.
Из советских АВУ, созданных для обработки сейсмической информации, можно назвать полуавтоматическое устройство ППСВР [24], предназначенное для обработки сейсмограмм в обычном виде (осциллографическая запись на фотометрах), и разработанный Н. Л. Гущиным, И. Ю. Клугманом, Ю. В. Коваленко и Б. Л. Лернером прибор ПСЗ-1 [21], обрабатывающий сейсмограммы, полученные методом отраженных волн и записанные на ферромагнитных пленках. Пример временного разреза, полученного на основе обработки сейсмограмм с помощью специализированного аналогового устройства, приведен на рис. 4.

Рис. 4. Пример временного разреза, полученного в результате автоматической обработки сейсмограмм с помощью аналогового вычислительного устройства
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'