Внедрение математических методов в практику геологоразведочных работ

Автоматизация обработки геологической информации тесно связана с развитием математических методов в геологии. Очень ярко важность математизации геологии освещена в книге А. В. Сидоренко [56].

С каждым годом возрастает необходимость перехода при изучении геологических явлений от приближенных, субъективных, описательных, качественных оценок к оценкам четким, строгим, объективным, количественным.

Отсутствие количественных характеристик приводит к тому, что в один ряд ставятся геологические явления совершенно разных масштабов. А. В. Сидоренко приводит следующий пример. До того как точными методами был определен абсолютный возраст геологических формаций, продолжительность эр и периодов представлялась более или менее одинаковой, в то время как на самом деле она отличалась в десятки и сотни раз.

Другой пример, приводимый автором [56], не менее разителен. Геологи считали, что в докембрии резко преобладают магматические процессы, а в последующие геологические эры - осадочные. Однако если выполнить по геологическим картам самые простые подсчеты площадей распространения магматических и осадочно-метаморфических пород в докембрии, то оказывается, что магматические породы в докембрии имели такое же подчиненное значение, как и в более поздние периоды. Этот вывод существенным образом изменяет подход к изучению докембрия.

Наиболее широко математические методы используются в геофизической разведке, исследующей различные геофизические поля (гравитационные, сейсмические, электрические, магнитные, радиоактивные), как естественно возникающие в земной коре, так и создаваемые искусственно. На основании этого исследования делаются выводы о строении недр, возможности наличия рудных тел, структур, с которыми могут быть связаны месторождения нефти и газа и т. п., а также в гидрогеологии.

В теории геофизической разведки различают прямые и обратные задачи. При решении прямых задач задаются некоторой моделью строения недр (например, полагают, что в пределах области исследования данного метода разрез представлен совокупностью параллельных пластов) и определяют тот эффект, который будет получен при исследовании данного поля. При решении обратных задач задан наблюденный эффект и необходимо сделать вывод о строении недр. Если прямые задачи решены для некоторого класса разрезов, то решение обратных задач во многих случаях сводится к последовательному сопоставлению замеренного эффекта с теоретическими результатами, полученными при решении прямых задач, до тех пор, пока не найдена будет такая модель строения недр (или некоторое множество моделей), для которой замеренный эффект достаточно близок к заданному.

Физические поля, исследуемые при геофизической разведке, описываются сложными дифференциальными, интегродифференциальными, интегральными уравнениями, и их решение привлекало внимание крупнейших математиков и физиков страны (П. П. Лазарева, О. Ю. Шмидта, В. А. Фока, А. Н. Тихонова, А. А. Ляпунова, М. М. Лаврентьева и др.).

Начало количественной интерпретации данных геофизических исследований было положено в двадцатых годах О. Ю. Шмидтом, принимавшим в то время участие в работе Особой комиссии по исследованию Курской магнитной аномалии (ОККМА). Эта комиссия, как известно, была создана по указанию В. И. Ленина. В районах Курской магнитной аномалии стали проводиться планомерные геофизические исследования - магнитная съемка, измерения с помощью вариометров Этвеша. Вначале, на основе качественного анализа полученных материалов, было сделано немало ошибочных заключений о строении недр - предполагалось, что "гребень" тяжелых масс проходит в районе максимума силы тяжести, в стороне от источника магнитной аномалии, ожидалась высокая (до 5) плотность пород, создающих гравитационные аномалии и т. п. Исходя из модели наклонного пласта, выбранной в соответствии с представлениями А. Д. Архангельского о геологическом строении района, О. Ю. Шмидт нашел аналитическое выражение для замеряемого при вариометрической съемке эффекта. Расчеты дали теоретические кривые, вполне сопоставимые с фактическими измерениями, произведенными П. М. Никифоровым. Используя в качестве характерного значения расстояния между точками максимума и минимума на кривой, О. Ю. Шмидт определил положение и параметры возмущающего тела (глубины залегания верхнего и нижнего краев пласта, мощность и угол наклона пласта, его относительную плотность). Относительная плотность тяжелых масс оказалась сравнительно небольшой (0,8). Было установлено, что источник гравитационной и магнитной аномалии один и тот же.

Результаты бурения показали хорошее совпадение данных интерпретации с фактическим строением недр. Это было триумфом строгого математического подхода к анализу полученных данных. Размеры настоящей брошюры не позволяют осветить теоретические работы О. Ю. Шмидта по космогонии и исследованию строения Земли в целом (как, впрочем, и работы в этих областях С. М. Молоденского, Н. Н. Парийского и др.).

Другим выдающимся советским геофизиком, Г. А. Гамбурцевым, был предложен ряд универсальных способов определения координат центра тяжести и массы возмущающего тела по наблюдениям гравитационного эффекта на поверхности - решения одной из основных обратных задач теории потенциала. Он разработал теорию и конструкцию механических интеграторов для вычисления гравитационного эффекта возмущающих тел, предложил решение прямых и обратных задач геометрической сейсмики.

Многие задачи теории геофизических исследований были решены советскими геофизиками А. А. Петровским, A. И. Заборовским, А. Н. Тихоновым, В. А. Фоком, B. Р. Бурсианом, А. П. Краевым, А. С. Семеновым, Л. М. Альпиным, А. П. Казанским, Б. А. Андреевым, Ю. П. Булашевичем и др.

Количественное истолкование данных стало, как правило, неотъемлемой частью геофизических исследований недр.

В настоящее время в поисково-разведочных работах особую актуальность приобрело исследование закономерностей пространственного распределения различных геохимических, минералого-петрографических и других характеристик геологических образований - исследование геохимических, минералого-петрографических и других полей. В связи с этим и в геолого-геохимической разведке встает вопрос о формулировке прямых и обратных задач и разработке методов их решения.

В геологических процессах принимает участие большое количество разнообразных факторов, и далеко не все из них можно учесть. Вследствие этого особое значение при решении задач поисков и разведки приобретает использование различных разделов теории вероятности (математической статистики и теории игр и статистических решений, теории информации и др.).

Применение статистических методов в геологии началось еще в прошлом веке, когда Ч. Лайель установил деление третичных отложений, взяв в качестве основного признака распространенность видов раковин, общих с раковинами современных отложений.

А. Б. Вистелиус [9] выделяет два периода в истории применения вероятностных методов:

1. "описательный", когда на основе изучения эмпирического материала находились статистические характеристики геологических объектов;
2. начинающийся со статьи А. Н. Колмогорова [28], когда помимо изучения вероятностных законов, имеющих место на практике, исследуют те процессы ("случайные процессы"), которые приводят именно к такому виду распределения вероятностей.

Математическая статистика находит применение при решении разнообразных задач поисков и разведки полезных ископаемых.

Были проделаны (и продолжаются в настоящее время) интересные и важные работы по изучению законов распределения химических элементов в горных породах, в частности, отмечена важная роль нормального и логнормального законов распределения. Эти работы позволили четко определить такие характеристики горных пород, как среднее содержание элемента, колеблемость (дисперсия) около среднего содержания и др. [51, 52].

Весьма интересные данные получены В. Я. Воробьевым, проводившим статистический анализ биогеохимических съемок в одном из районов Южного Урала.

В обычных условиях распределение элементов в гумусовом горизонте почвы соответствует нормальному (гауссову) закону, если же профиль пересекает месторождения руд, распределения становятся асимметричными и приближаются к логнормальному.

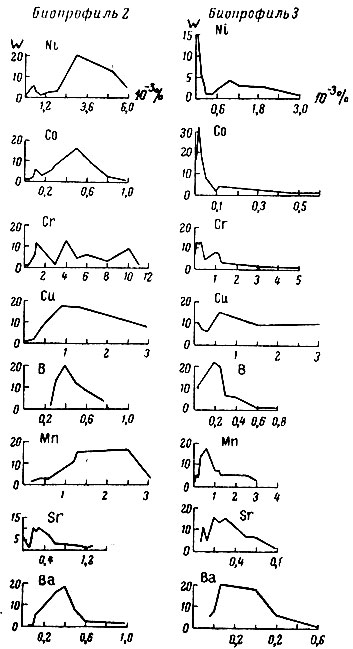
Рис. 6. Сопоставление кривых распределения ряда элементов в гумусовом горизонте почвы по двум профилям (ω - число образцов с данным значением концентраций).

На рис. 6 приведены кривые распределения ряда элементов (Ni, Co, Cr и др.) в гумусовом горизонте по двум биопрофилям - второму и третьему. Второй профиль пройден в основном над безрудными участками и распределение элементов подчиняется гауссову закону. Третий же профиль прошел над коренными породами, характеризующимися повышенным содержанием никеля, кобальта и хрома, вследствие чего распределение элементов в почве становится асимметричным, соответствующим логнормальному.

В конце 40-х годов были разработаны на основе понятий теории вероятности численные характеристики тесноты связи между членами парагенезов (работы А. Б. Вистелиуса и др.). Это позволило, в частности, на основе использования корреляционных связей между легко определимыми главными элементами руд и рассеянными в рудах элементами, разработать методики косвенного подсчета запасов элемента примеси по запасам главного элемента. Нередко определение связей между различными компонентами горных пород позволяет сделать новые выводы о генетических особенностях горных пород.

Большую помощь при анализе структуры кристаллических тел и выделении рудоносных участков оказывают геохимические карты тренда - карты распределения процентного содержания того или иного элемента в горных породах. Эти карты характеризуют основные направления, главные тенденции в размещении различных руд, в связи с чем и получили название "карт тренда". При построении карт тренда первичный материал подвергают определенной обработке (осреднению по специальной схеме, позволяющей существенно снизить роль случайных факторов и т. д.). На рис. 7 приведены карты тренда для двух элементов по южной части Волынского габбро-анартозитового плутона Украинского кристаллического щита, составленные в проблемной лаборатории геологического факультета Киевского университета (М. И. Толстой, И. М. Остафийчук и др.). На картах четко выделяются приуроченные к краевым частям плутона области повышенной концентрации, представляющие собой приконтактовые его зоны. Эти зоны соответствуют областям предполагаемых подводящих каналов, выделяемых также и по данным гравиразведки.

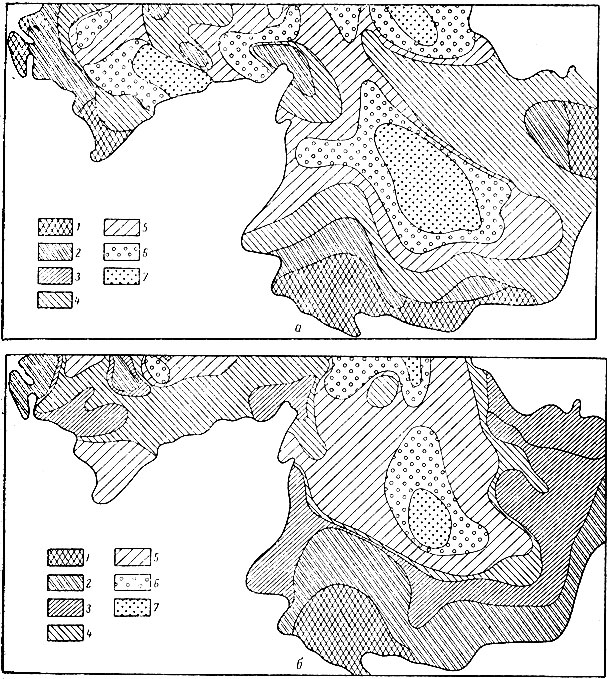
Рис. 7. Геохимические карты тренда для никеля и титана южной части одного из плутонов Украинского кристаллического массива. а - содержание Ni (%): 1 - 0,0025 - 0,005, 2 - 0,00125 - 0,0025, 3 - 0,00063 - 0,00125, 4 - 0,00032 - 0,00063, 5 - 0,00016 - 0,00032, 6 - 0,00008 - 0,00016, 7 - 0,00004 - 0,00008; б - содержание Ti (%): 1 - 0,9 - 1,6, 2 - 0,5 - 0,9, 3 - 0,28 - 0,5, 4 - 0,16 - 0,28, 5 - 0,09 - 0,016, 6 - 0,05 - 0,09, 7 - 0,028 - 0,05

Большое значение имеет разработка четких количественных характеристик в палеонтологии. Определение видов, подвидов и других таксономических единиц на основе описания единичных образцов (в котором часто большую роль играют субъективные факторы) в настоящее время приводит к весьма нежелательной неоднозначности в стратиграфическом расчленении и корреляции отложений. Эти недостатки можно преодолеть, если рассматривать вид как политипическую ассоциацию, изучение которой возможно лишь на основе всестороннего анализа совокупностей, относимых к данному виду или подвиду, с учетом их возможностей изменчивости (индивидуальной, географической, экологической, изменчивости, обусловленной цикловым и половым диморфизмом, и т. д.), анализа, который возможен на основе применения математической статистики, на основе объективной числовой характеристики видов. Разработка математических критериев важна и для установления ареалов распространения родов и видов, анализа их эволюционных изменений, выяснения генетических связей между группами видов, родами и другими таксономическими единицами, отнесения "промежуточных форм" к тому или иному виду, расчленения и сопоставления разрезов и др.

Такая математизация палеонтологии, безусловно, приведет к ревизии ряда выделенных видов и подвидов, а возможно, и более крупных таксономических категорий.

В Советском Союзе методы математической статистики использовались при изучении фораминифер, брахиопод, пелеципод, гастропод, белемнитов, остракод и др. [45].

Из зарубежных особого внимания заслуживают работы Р. Реймвита (Швеция), успешно применявшего мультивариантный биометрический анализ при изучении остракод и фораминифер из верхнемеловых и неогеновых отложений Нигерии (Западная Африка) [74].

Работы, связанные с разработкой количественных характеристик и использованием статистических методов исследования, ведутся и в области тектоники - при изучении морфологических параметров геологических структур, пород, связи между нефтегазоносностью и количественными характеристиками геологического строения района, при исследовании трещиноватости горных пород и т. п. [7, 46].

Особенно важное значение имеет применение математических методов и, в частности, математической статистики, при выработке методики опробования, разведки и подсчетов запасов месторождений полезных ископаемых - при оценке качества химических анализов, определении необходимых размеров проб и интервалов между ними, исследовании точности определения параметров.

Созданию моделей вероятностных процессов в геологии посвящен ряд работ А. Н. Колмогорова [28, 29], А. Б. Вистелиуса и О. В. Сарманова [8].

Очень важным и интересным новым направлением использования математических методов в геологии является совершенствование логики научного познания в геологических исследованиях, в частности, разработка научно обоснованного подхода к геологическим классификациям.

Широкий интерес у геологов вызвали проводимые под руководством Ю. А. Косыгина работы по уточнению (формализации) геологических понятий [30, 31].

В последние годы при решении геологических задач нашли применение новые математические дисциплины - теория информации, теория игр и статистических решений [10, 20, 38, 39, 41, 69, 70].