Применение ЭЦВМ для решения задач поисков и разведки месторождений полезных ископаемых
В настоящее время как у нас, так и за рубежом электронные цифровые вычислительные машины находят все большее применение при решении задач, связанных с поисками и разведкой месторождений полезных ископаемых.
Больше всего, по объему машинного времени, по-видимому, решалось задач разведочной геофизики. В первую очередь это касалось прямых задач геофизической разведки, разработки теории геофизических исследований.
В области сейсморазведки ведутся работы по решению прямых задач на базе волнового уравнения (И. Г. Петрашень и др.). В гравиразведке на ЭЦВМ решались прямые задачи для трехмерных выпуклых тел. В области электроразведки в большом объеме проводились работы, связанные с разработкой теории частотных электромагнитных зондирований (А. Н. Тихонов, Л. Л. Ваньян и др.), расчетом кривых зондирования в случае сложных разрезов для методов электроразведки постоянным током (ВЭЗ, ДЭЗ) и др.
В промысловой геофизике ЭЦВМ применяются при решении прямых задач теории каротажа - работы Л. М. Альпина (разработка теории каротажа сопротивлений), А. А. Кауфмана, Г. И. Зверева (разработка теории индукционного каротажа), С. А. Кантора, С. А. Денисика, Р. А. Резванова, Б. Е. Лухминского, И. Г. Дядькина и др. (разработка теории радиоактивного каротажа). В решении задач радиоактивного каротажа хорошие результаты дает метод статистических испытаний (метод Монте-Карло), реализация которого без современной вычислительной техники практически невозможна.
Весьма интересны работы по созданию методов автоматической обработки геофизической информации на основе применения ЭЦВМ. Наибольшее число их связано с обработкой данных гравиразведки. Первые работы [68, 71, 75] относятся к первой половине 50-х годов. В СССР электронные вычислительные машины для обработки данных гравиразведки впервые стали применять сотрудники кафедры геофизики МГУ [4, 44] и АН БССР [61.
Наиболее успешно с помощью ЭЦВМ проводится трансформация гравитационных и магнитных полей (пересчет в верхнее и нижнее полупространство, вычисление высших производных и т. п.). На основе трансформации полей во многих случаях удается выделить локальные аномалии на фоне региональных или же, наоборот, снять мелкие, носящие местный, случайный характер элементы и рельефно выделить аномалии, обусловленные более крупными тектоническими единицами.
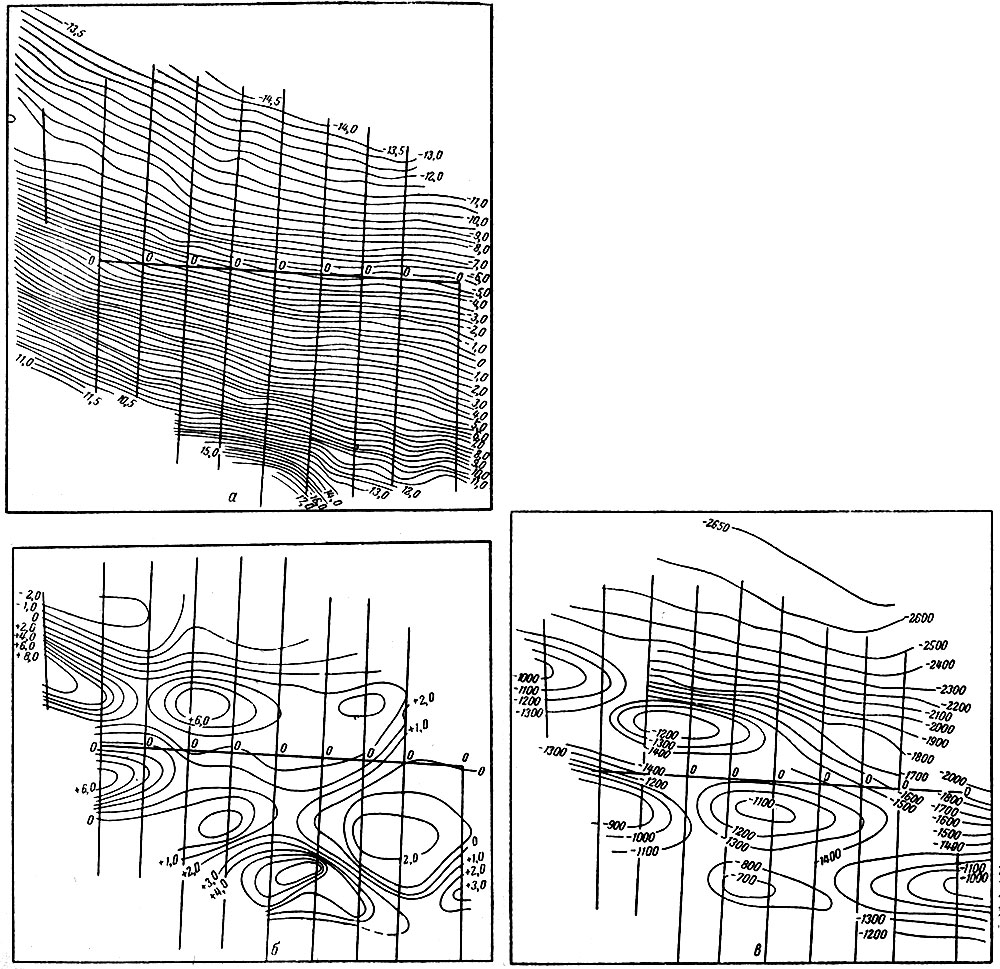
Рис. 8. Пример трансформации гравитационного поля (по Н. Б. Сажиной). а - карта изоаномал силы тяжести; б - карта остаточных аномалий; в - структурная карта по опорному сейсмическому горизонту.
В качестве иллюстрации геологической эффективности трансформации гравитационного поля на рис. 8 отражены материалы интерпретации гравиметровой съемки в одном из районов (по Н. Б. Сажиной). На рис. 8, а приведена карта изоаномал силы тяжести. Вследствие сильного влияния регионального фона локальные аномалии затушеваны - выделение структур непосредственно по карте изоаномал не представляется возможным. На рис. 8, б дана карта остаточных аномалий, полученная путем трансформации поля - снятия регионального фона по методу Саксова-Нигарда. На ней четко выделяется ряд локальных аномалий, хорошо согласующихся со структурами, выявленными сейсморазведкой (рис. 8, в).
Трансформации гравитационных и магнитных полей посвящено большое количество работ. Многие из разработанных методов машинной трансформации полей используются в практике геофизической разведки. Возможность использования ЭЦВМ для трансформации полей и других методов обработки данных грави- и магниторазведки стимулировало разработку более совершенных вычислительных схем (работы В. Н. Страхова, Г. И. Каратаева, М. Г. Сербуленко и др.).
Очень важны работы, посвященные определению параметров возмущающих тел. Теоретические основы этим работам положили исследования А. Н. Тихонова, М. М. Лаврентьева, посвященные анализу так называемых некорректно поставленных задач.
С помощью ЭЦВМ у нас в стране решаются такие задачи, как определение по гравитационным и магнитным аномалиям элементов залегания прямоугольного пласта бесконечной мощности, построение контактной гравитирующей поверхности в случае постоянной и переменной плотности покрывающих пород, определение плотности промежуточного слоя по гравиметрическим данным, пересчет полей из гравитационного в магнитное, вычисление корреляционных функций полей.
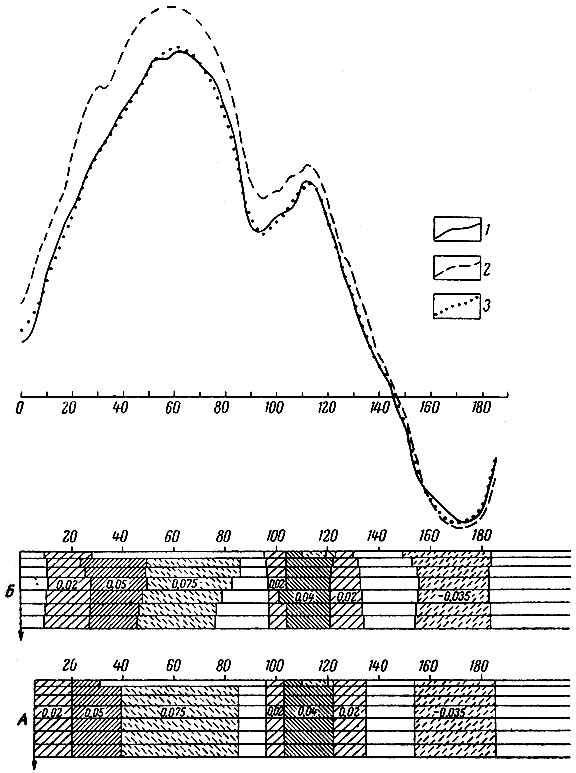
Рис. 9. Машинная интерпретация данных гравиразведки - уточнение плотностного разреза. А - исходный разрез, полученный в результате обычной интерпретации' В - разрез, уточненный с помощью ЭЦВМ; 1 - фактическая кривая; 2- кривая, соответствующая разрезу А; 3 - кривая, соответствующая разрезу Б
На рис. 9 представлен пример уточнения плотностного разреза с помощью ЭЦВМ по одному из районов Украинского щита. На этом рисунке показан плотностный разрез А, построенный О. Б. Гиитовым на основе "обычной" интерпретации данных гравиразведки (2). Этот разрез использовался в качестве начального приближения при машинной интерпретации гравитационной аномалии методом скорейшего спуска по программе, разработанной Е. Г. Булахом. В результате получен уточненный плотностный разрез Б. Если аномалия 2, соответствующая разрезу А, существенно отличается от фактической i, то кривая 5, рассчитанная для разреза Б, практически совпадает с нею.
Весьма эффективно использование ЭЦВМ для внесения в данные гравиразведки поправок за рельеф. Так, до применения этих машин проведение крупномасштабной гравиметровой съемки в пределах Карпат встречало серьезные затруднения. Использование машинной обработки данных гравиразведки позволило получить совершенно новые сведения о тектоническом строении региона и более рационально направить дальнейшие исследования, связанные с .поиском нефтегазоносных структур.
Очень интересным направлением, практическое осуществление которого возможно лишь на основе использования современной вычислительной техники, является выделение слабых аномалий на фоне помех. Этой проблеме в грави- и магниторазведке посвящены работы И. Г. Клушина [26] и других исследователей.
Работы по применению статистических методов для выделения полезных аномалий на фоне случайных помех при интерпретации данных электроразведки ведутся под руководством А. Г. Тархова [57]. Интерпретации кривых ВЭЗ с помощью электронных цифровых вычислительных машин посвящены работы Р. Д. Юкна [62], В. О. Урысона, Хомилиуса и др.
Ведутся работы по применению цифровых вычислительных машин для обработки данных сейсморазведки. Основная трудность, которая сдерживает широкое применение их для автоматической обработки сейсмограмм, связана с тем, что последние характеризуются большим объемом информации: при преобразовании в цифровую форму, сейсмограмме соответствует массив, состоящий из нескольких десятков тысяч чисел, что намного превышает объем оперативной памяти ЭЦВМ. Обработка больших массивов информации требует, как уже рассматривалось выше, многоканальных ЭЦВМ. Поскольку с ростом объема обрабатываемой информации время на обработку растет (и чаще всего в степенной зависимости), интерпретация сейсмограмм с помощью цифровых вычислительных машин требует больших объемов машинного времени и (при желании проведения этой интерпретации оперативно) большего быстродействия, чём то, которым обладают основные серийные отечественные ЭЦВМ.
В настоящее время проведена большая работа по созданию математических моделей различных звеньев обработки сейсмограмм и их реализации на ЭЦВМ - корреляция волн, математическая фильтрация, обработка сейсмограмм по методу регулированного направленного приема, построение разрезов, а также определение эффективных скоростей и статистических поправок по выделенным воланам (оси синфазности при этом проводит человек) и т. д. (И. И. Гурвич, Ф. М. Гольцман, С. В. Гольдин и др.).
По-видимому, автоматизация обработки сейсмограмм будет решена на основе комплексного использования аналоговых вычислительных машин и ЭЦВМ. В связи с тем, что обработка на АВУ для многих задач более экономична и требует меньшего времени, чем обработка на ЭЦВМ, она удобна для массовой трансформации сейсмограмм в разрезы. ЭЦВМ целесообразно применять для "прецизионной", максимально тщательной обработки, реализуя алгоритмы сложной логической структуры.
Цифровые вычислительные машины успешно применяются для таких видов обработки, как построение синтетических сейсмограмм по данным акустического каротажа, корреляция скоростей с данными анализов кернов и др.
Как в СССР, так и за рубежом ведутся работы по созданию методов автоматической обработки данных геофизических исследований буровых скважин на основе применения ЭЦВМ. Уже предложено большое число алгоритмов, реализующих различные этапы и звенья обработки каротажных диаграмм: в различных диаграммах оценка качества материалов, согласование глубин, расчленение разреза (литологическое, стратиграфическое и т. д.), выделение в разрезе коллекторов нефти и газа или же других геологических объектов, имеющих практический интерес, отсчет характерных значений (значений регистрируемой величины, используемых при дальнейшей обработке), переход от характерных значений к физическим параметрам пласта (удельное электрическое сопротивление, пористость и др.), корреляция каротажных диаграмм и т. п. Эти алгоритмы применимы для обработки данных различных методов: электрического каротажа (в частности, для обработки диаграмм бокового каротажного зондирования) и диаграмм микрокаротажа, радиоактивного каротажа и т. п. [35- 37, 41].
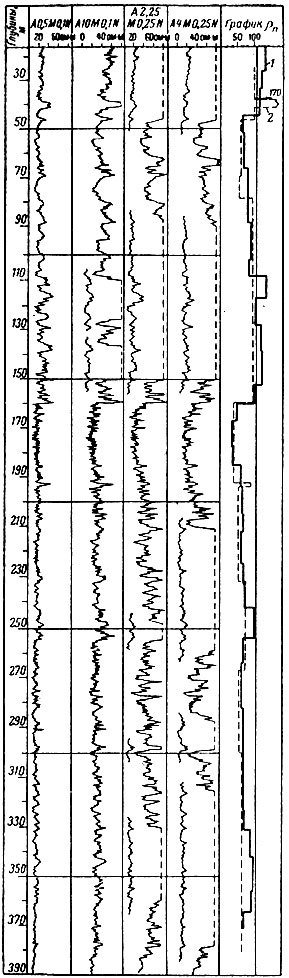
Рис. 10. Машинная интерпретация диаграмм бокового каротажного зондирования. Покутская опорная скважина. Результаты интерпретации, полученные: 1 - машиной, 2 - человеком
На рис. 10 приведен пример машинной интерпретации диаграмм бокового каротажного зондирования по Покутской опорной скважине в Западной Украине (совместные работы Киевской экспедиции УкрНИГРИ и Института кибернетики АН УССР). В соответствии с заданным алгоритмом ЭЦВМ выделила пласты, произвела отсчет характерных значений КС с различных диаграмм, сопоставила фактическую кривую БКЗ с палеточными и определила удельное сопротивление каждого пласта. Вся обработка диаграмм на машине, выполняющей 20 тыс. операций в секунду, осуществлялась менее 5 мин. На рис. 11 показано сопоставление результатов интерпретации, полученных машиной и человеком.
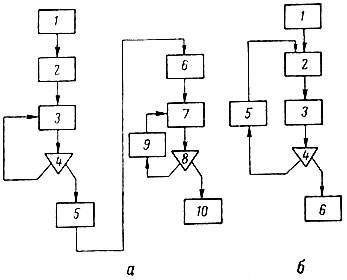
Рис. 11. Блок-схемы некоторых алгоритмов автоматической обработки каротажных диаграмм. а - схема машинной интерпретации диаграмм бокового каротажного зондирования; б - схема трансформации кривой НГК в кривую пористости
Различие между результатами интерпретации машиной и человеком невелико - оно не больше различия в результатах обработки, осуществляемой независимо разными интерпретаторами. Интерпретация, произведенная машиной, отличается большей деятельностью - выделено и проинтерпретировано большее число пластов. Тонкий пласт в интервале 38-42 м, выделенный интерпретатором, не зафиксирован машиной в связи с тем, что данной программой выделение тонких пластов не предусматривалось. Интерпретация кривых БКЗ по палеткам машиной осуществлялась с большей точностью, чем человеком. Кроме определения удельного сопротивления пласта при сопоставлении фактической кривой БКЗ с палеточной осуществлялась количественная оценка: расхождения между кривыми. Эта величина (расхождение) использовалась для уточнения 1 методики отсчета характерных значений КС - программа предусматривала "самонастройку".
Схема применения вычислительных машин при автоматической обработке диаграмм БКЗ следующая (рис. 11, а).
- Диаграммы каротажа сопротивлений, а также кавернограмма преобразуются в цифровую форму (например, с помощью специализированного преобразователя). При этом каждой диаграмме будет соответствовать последовательность чисел - отсчеты значений регистрируемого параметра через равные интервалы. Оцифрованные таким образом кривые каротажа вводятся в ЭЦВМ (блок 2).
- Выбирается базовая кривая кажущегося сопротивления (обычно кривая КС, снятая градиент-зондом длиною 1 м), и по этой кривой расчленяется разрез на пласты. Границы отбиваются по экстремальным точкам, которым на кривой КС соответствуют экстремумы - максимумы и минимумы, причем на кривой отмечаются не все экстремумы, а только те (так называемые "существенные экстремумы"), которые удовлетворяют ряду дополнительных условий: доминирование над соседними экстремумами, достаточная величина отклонения аномалии, связанного с данным экстремумом, и т. п. (блок 2).
- Отсчитываются характерные значения КС против выделенных пластов по данной диаграмме (блок 3).
- Проверяется, со всех ли диаграмм КС отсчитаны характерные значения (блок 4). Если еще не все диаграммы обработаны, то подготавливается к обработке очередная кривая и управление передается блоку 3.
- Отсчитывается фактический диаметр против выделенных пластов по кавернограмме (блок 5). Таким образом для каждого выделенного пласта оказываются отсчитанными совокупность значений КС (фактическая кривая зондирования) и фактический диаметр скважин. Эти данные (при наличии сведений о длинах зондов и удельном сопротивлении бурового раствора) достаточны для осуществления количественной интерпретации материалов БКЗ.
- Выбирается фактическая кривая зондирования для первого пласта (блок 6).
- Последовательно сопоставляется фактическая кривая зондирования с теоретической (теоретические кривые зондирования хранятся в памяти ЭЦВМ в виде специальных таблиц) до тех пор, пока не будет найдена теоретическая кривая, наилучшим образом совпадающая с фактической (блок 7). Параметры разреза, соответствующие найденной теоретической кривой (удельное сопротивление пласта и др.), и являются искомым ответом.
- Проверяется, для всех ли пластов произведена количественная интерпретация (блок 8).
- Если пласты не исчерпаны, выбирается очередная фактическая кривая зондирования (блок 9) и управление передается блоку 7.
- По окончании интерпретации печатаются результаты произведенной обработки каротажных диаграмм - границы выделенных пластов, отсчитанные характерные значения КС, значения удельного сопротивления пласта и параметров зоны проникновения, найденные в результате сопоставления фактической кривой зондирования с теоретическими, и т. п. (блок 10).
На рис. 12 приведен пример машинной обработки диаграмм радиоактивного каротажа - определения по кривой нейтронного гамма-каротажа пористости известняков. Алгоритм предусматривал внесение различного рода поправок в показания НГК (внесение поправок за инерционность аппаратуры, вычитание фона естественного гамма-излучения и т. п.), определение по каверномеру толщины глинистой корки, выбор в соответствии с найденным значением толщины глинистой корки палетки для количественной интерпретации НГК и, наконец, определение пористости.
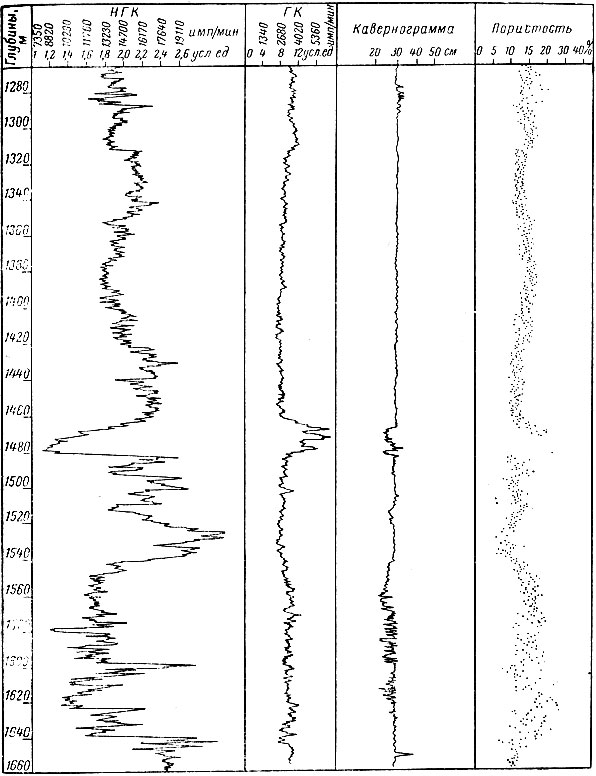
Рис. 12. Машинная обработка диаграмм нейтронного гамма-каротажа
График изменения пористости с глубиной, полученный на основе обработки диаграммы нейтронного каротажа, позволяет не только найти среднее значение пористости против того или иного интервала, но и колеблемость (дисперсию) этого параметра около другого значения. Колеблемость может иметь самостоятельное значение (кавернозные известняки во многих случаях характеризуются повышенным значением колеблемости).
Трансформация кривой НГК в кривую пористости крайне громоздка при осуществлении ее вручную, машина же выполняет ее в течение 1-2 мин, при этом достигается выигрыш во времени в несколько десятков (до 100) раз и выигрыш в стоимости обработки в несколько раз (до 10).
В данном случае при обработке диаграмм нейтронного гамма-каротажа была применена следующая схема (см. рис. 11, б).
- Из последовательности значений зарегистрированной интенсивности излучения выбирается первое снизу значение (каротаж производится снизу вверх и в этой же последовательности и ведется обработка, блок 2).
- В данное значение вносятся поправки (за инерционность аппаратуры, за нелинейность шкалы и т. п.), вычитаются показания гамма-каротажа (гамма-фон), осуществляется переход от абсолютных значений интенсивности к относительным. Все это может быть названо предварительной обработкой величины интенсивности (блок 2).
- Найденное в результате предварительной обработки значение интенсивности сопоставляется с палетками и находится соответствующая величина пористости (блок 3).
- Проверяется, вся ли кривая НГК просмотрена (блок 4).
- Если просмотр кривой не закончен, выбирается очередное значение интенсивности (блок 5) и осуществляется переход к блоку 2%.
- Если обработка кривой закончена, то результаты трансформации - кривой НГК в кривую пористости выдаются на печать (блок 6).
В УкрНИГРИ совместно с Институтом кибернетики АН УССР был проведен опыт реализации на ЭЦВМ самоорганизующегося алгоритма обработки промыслово-геофизической информации - машина по заданной эталонной информации находила структуру алгоритма, решающего данную задачу обработки каротажных диаграмм [41].
Первой самонастраивающейся программой обработки промыслово-геофизических данных, по-видимому, была реализованная на машине "Урал-1" программа интерпретации кривых БКЗ, предусматривающая уточнение в процессе интерпретации значения удельного сопротивления бурового раствора [17].
По инициативе Ш. А. Губермана началось применение самообучающихся программ диагностического типа для разделения нефтегазоносных и водоносных пластов и других задач геологической диагностики [34].
В одном из экспериментов, соответствующем благоприятным условиям, по результатам обучения на материалах по 90 пластам (по 45 нефтеносным и 45 водоносным) при последовавшей потом диагностике 200 пластов машина сделала всего четыре ошибки, в то время как при обычной интерпретации было допущено 20 ошибок.
В 1962 г. за рубежом в нефтяной промышленности (главным образом в США) работало свыше 300 электронных цифровых вычислительных машин.
На основе изучения статистики различных параметров структур (отношение больших и малых осей, ориентация осей структур и т. п.) с помощью ЭЦВМ находится рациональная последовательность поисково-разведочного бурения.
Большую помощь оказывают цифровые вычислительные машины при региональных геологических обобщениях. Кодируются - записываются в форме, удобной для ввода в машину, такие данные, как название или номер скважины, ее местоположение, реперные горизонты, данные по опробованию пластов, особенности конструкции скважины, наличие нефтепроявлений, виды проводившихся геофизических исследований и т. п.
Использование информационно-поисковых систем или ЭЦВМ позволяет быстро получить различные материалы, необходимые для решения геологопоисковых задач - перечень скважин, вскрывших в данном районе продуктивный или маркирующий горизонт, план скважин в необходимом масштабе, перечень скважин с указанием интервалов опробования пласта и результатами опробования и т. п.
В США в настоящее время проводится подготовка по переводу в кодированную форму материалов по 140 тыс. скважин.
С помощью ЭЦВМ осуществляется построение структурных карт, карт равных мощностей и других карт в изолиниях, а также анализ карт.
Рассмотрим задачу построения структурных карт с помощью ЭЦВМ. Имеется ряд точек, координаты которых х и y известны. Расположение этих точек в плане произвольно. Для каждой известна глубина залегания некоторой поверхности (например, кровли или подошвы определенного стратиграфического горизонта). На основе этих данных электронная цифровая вычислительная машина находит поверхность некоторого класса, наименее уклоняющуюся от заданных точек. Найденную поверхность называют аппроксимирующей. Уравнение аппроксимирующей поверхности может быть записано в виде:
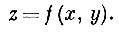 (5)
(5)Класс поверхностей определяется видом функции f (x, y).
Наиболее часто полагают, что эта функция является полиномом от двух переменных:
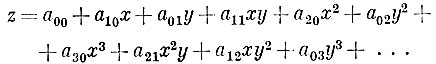 (6)
(6)В этом случае задача нахождения аппроксимирующей поверхности сводится к определению коэффициентов а00, а01, а10, а20, а02, а11 ... Коэффициенты находят на основе решения системы линейных уравнений методом наименьших квадратов. Число коэффициентов не должно превышать числа точек, для которых известны альтитуды. Число коэффициентов, подлежащих определению, зависит от степени полинома, причем эта зависимость выражается простой формулой:
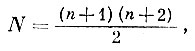 (7)
(7)где N - число коэффициентов; n - степень многочлена.
При n = 1 полином имеет вид:
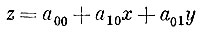 (8)
(8)и выражает уравнение плоскости.
При n = 2 полином имеет вид:
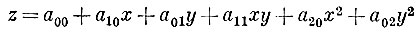 (9)
(9)и определяет поверхность второго порядка (эллипсоид, параболоид, гиперболоид и др.).
Следует отметить, что поверхность более высокого порядка включает как частный случай поверхности более низких порядков. Так, если реальная поверхность в рассматриваемом участке очень близка к плоскости, то мы найдем, что коэффициенты при одночленах второй степени (а11, а20, а02) близки к нулю, т. е., осуществляя поиск поверхности второго порядка, в данном случае мы приходим к плоскости (поверхности первого порядка) и полином (9) превращается (математики в таких случаях говорят "вырождается") в полином (8).
При построении карт изолиний вручную применяют линейную интерполяцию, т. е. исходят из того предположения, что в данном участке поверхность мало отличается от плоскости. Однако очень часто такое приближение оказывается недостаточным и, как мы увидим ниже, линейная интерполяция вносит систематические ошибки. Полагая, что поверхность имеет более сложный вид (соответствует полиному второго, третьего и более высокого порядка), мы точнее определяем геометрию ее.
Если число точек, по которым проводятся изолинии, менее шести, мы не выходим за пределы возможности линейной интерполяции, при числе точек от шести до Девяти мы в состоянии подобрать поверхность второго порядка. В соответствие с формулой (7) зависимость степени аппроксимирующего полинома от числа точек характеризуется табл. 5.
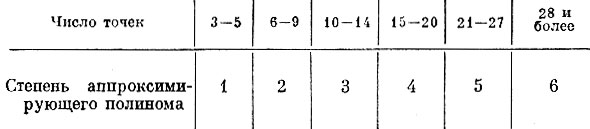
Таблица 5
Полиномы степени выше шестой используются сравнительно редко.
Следует сразу обратить внимание на то, что если реальная поверхность достаточно сложна, например, выражается поверхностью третьего, четвертого или даже более высокого порядка, а число точек невелико, восемь-девять (с такой ситуацией иногда приходится сталкиваться при построении структурных карт по данным глубокого бурения), то принципиально не существует никакого способа, будь то "ручной" или "машинный", который бы на основании данных о глубинах в этих восьми-девяти точках позволил в общем случае определить параметры искомой поверхности. Имеющейся информации недостаточно для полного решения задачи, и мы вынуждены либо получить дополнительную информацию (пробурить еще одну или несколько скважин), либо ограничиться нахождением некоторой "модели" - приближенной поверхности, которая выражает основные черты реальной поверхности, но в то же время может отличаться от последней в деталях.
Итак, при решении задачи определения аппроксимирующей поверхности искомого горизонта входная информация должна состоять из трех последовательностей (массивов): значений координат х и y и глубин z, т. е. соответствовать форме:
Координата х Координата y Глубина z
Кроме того, необходимо чтобы число значений в указанных массивах (их длина) было не менее некоторого заранее заданного числа. Так, если осуществляется поиск поверхности не менее второго порядка, то длина массивов должна быть не менее шести.
Примером таблицы входной информации при решении рассматриваемой задачи может служить табл. 6 (координаты х и y условные).

Таблица 6
После того как уравнение аппроксимирующей найдено, на ЭЦВМ может быть осуществлен расчет значений глубины для любой системы точек в пределах рассматриваемого участка, например, по некоторой квадратной сетке с достаточно малым шагом, так что построение изолиний по этим данным можно будет осуществить весьма просто. На цифровой вычислительной машине могут быть прослежены изолинии и выданы координаты изолиний, например, по определенным профилям. Особенно удобно получение структурных карт с помощью ЭЦВМ, если имеется выходное устройство, способное вычерчивать изолинии.
Таким образом, схема применения цифровых вычислительных машин при построении структурных карт несложна и сводится к последовательному выполнению следующих этапов.
- Ввод в ЭЦВМ координат и соответствующих им глубин.
- Нахождение значений неизвестных коэффициентов аппроксимирующего полинома на основе решения системы линейных уравнений.
- Вычисления значений найденного полинома по определенной системе. Нахождение, если это требуется, координат изолиний.
- Выдача полученных данных на печать.
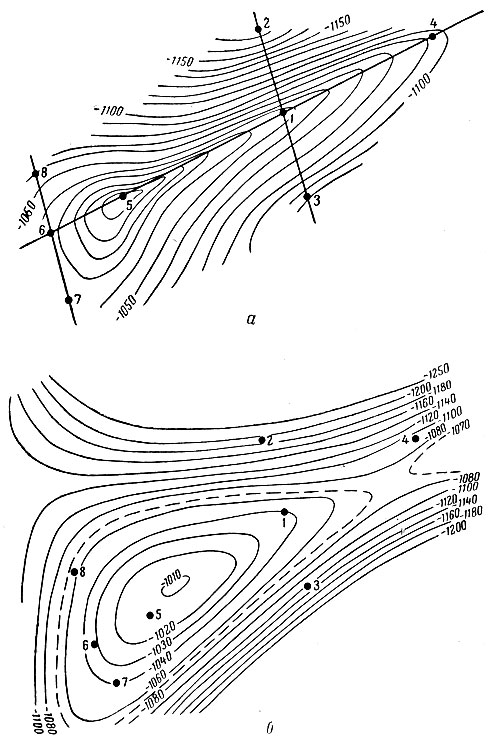
Рис. 13. Сопоставление структурных карт, построенных на основе линейной интерполяции (а) и с помощью ЭЦВМ (б)
На рис. 13 приведено сопоставление структурных карт одной из площадей Черноморской впадины, построенных обычным путем на основе линейной интерполяции (рис. 13, а) и с помощью ЭЦВМ (рис. 13, б). Прямыми линиями на рис. 13, а проведены профили бурения. Обращает на себя внимание, что при линейной интерполяции изолинии подтягиваются к профилям бурения. Причина этой систематической ошибки становится ясной, если обратиться к рис. 14: прямая, соединяющая две точки поверхности, проходит внутри последней, и точка пересечения этой линии с секущей горизонтальной плоскостью ближе к линии профиля, чем соответствующая точка пересечения реальной поверхности с секущей плоскостью.
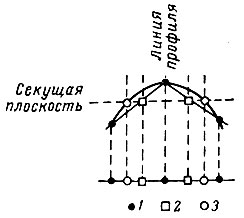
Рис. 14. Смещение изолиний к линии профиля при линейной интерпретации. 1 - точки, в которых глубина известна; 2 - положение точек изолиний при линейной интерпретации; 3 - фактическое положение изолиний
Мы рассмотрели случай, когда поверхность не осложнена дизъюнктивными нарушениями. Но и в более сложных случаях также можно осуществлять построение структурных карт "на основе применения ЭЦВМ; при этом машина может находить уравнения поверхностей, соответствующих различным крыльям и блокам структур, поверхности сбрасывателей и других, также определить линии пересечения этих поверхностей.
Заметим также, что после того как параметры аппроксимирующих поверхностей различных геологических границ найдены, они могут быть использованы не только для построения структурных карт, но и для решения многих других задач (определения объема геологических тел, что важно при подсчете запасов полезных ископаемых, разделения локальных и региональных элементов рельефа исследуемой поверхности и т. п.).
Естественно, что построение в карт изолиний с помощью ЭЦВМ может быть осуществлено не только по данным о высотных отметках, но и по любым цифровым характеристикам свойств и горных пород, нефтей, газов, вод и т. п. В частности, может быть автоматизировано построение геохимических карт тренда.
Аппроксимация некоторой поверхности, простой для вычисления функций, используется не только для построения карт изолиний этой поверхности, но и для анализа - выделения локальной аномалии на фоне региональной. Локальные аномалии получаются, например, как разность между полиномом высокой (например, шестой) степени, которым аппроксимируется данная поверхность, полиномом малой (например, третьей) степени, с которой связан региональный фон. Полином третьей степени при этом также находят как результат аппроксимации но более грубой) данной поверхности. Функции, получаемые в результате аппроксимации, удобно дифференцировать, интегрировать и производить над ними другие математические операции.
Большое число программ машинного счета для решения различных петро-химических и минералогических задач (оценка особенностей парагенетических типов минералов, связей между содержанием главных компонентов в породах и минералах, связей между составом и свойствами пород и минералов и т. п.) созданы и используются в Институте геологии и геофизики СО АН СССР.
Разработан ряд программ статистической обработки данных: определение основных выборочных статистических параметров - среднее, дисперсия, стандартное отклонение, асимметрия, эксцесс и ошибки репрезентативности (В. А. Кутолин, В. В. Колмогоров), расчет коэффициентов парных линейных корреляций (Н. Л. Добрецов, В. В. Хлестов), множественная корреляция (Р. С. Стрелко и Ф. М. Бородкин) и др. Кроме того, составлены программы массового пересчета химических анализов (А. Е. Телешов, Е. П. Пучков), пересчета химических анализов породообразующих минералов на кристаллохимические формулы и т. д. [5].
Большой интерес представляют работы по созданию вычислительных схем при автоматическом выделении однородных геологических объектов в разрезах скважин, по профилям и т. д. (Д. А. Родионов, В. Я. Воробьев и др.). В основу такого расчленения положена следующая идея: два соседних интервала (на профиле, в разрезе скважин) считаются принадлежащими к различным геологическим объектам, если гипотеза о том, что полученные для этих участков характеристики статистически однородны, отвергается. Если же такая гипотеза не отвергается, то считается, что оба участка принадлежат одному и тому же геологическому объекту. Практически проверка гипотезы сводится к вычислению для анализируемой границы определенного статистического критерия v1, и если значение v больше некоторой заранее заданной величины vкр, то гипотеза отвергается.
1 (Аналитическое выражение для параметра v сравнительно громоздко (см., например, [53]).)
Выделение границ геологических объектов геологами и геофизиками, особенно если оно производится по сложному комплексу характеристик, зависит от субъективных факторов. Применяя же машинные методы выделения однородных в том или ином геологическом смысле объектов, мы решаем эту задачу на основе объективных критериев.
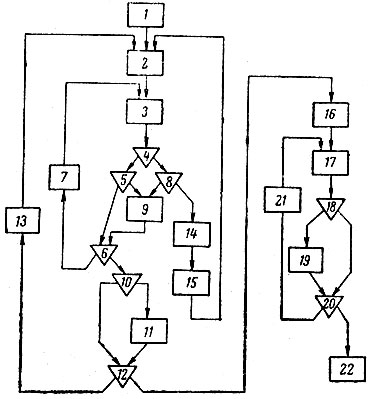
Рис. 15. Блок-схема одного из алгоритмов статистического расчленения разреза на однородные совокупности
На рис. 15 показана блок-схема одного из таких алгоритмов1. Чтобы сократить объем вычислений, вначале допускается возможность задания ряда фиктивных границ (например, путем разбивки разреза на равные интервалы). Задача решается следующим образом.
1 (Алгоритм, соответствующий рис. 15, автор применял при расчленении диаграмм радиоактивного каротажа.)
- Выбирается первый интервал от начальной точки до первой фиктивной границы (блок i).
- Выбирается первая из возможных границ внутри данного интервала (проведение границы возможно между двумя соседними точками, для которых получены характеристики геологического объекта, так как число таких точек всегда ограничено, число возможных границ не так уж велико) (блок 2).
- Вычисляется значение критерия v (блок 3).
- Проверяется, было ли сохранено значение критерия v для предыдущей границы данного интервала (блок 4). Если да, то осуществляется переход к блоку 5, если же нет - переход к блоку 5.
- Проверяется гипотеза об однородности (блок 5). Если она не отвергается (v> vкр), то происходит переход к блоку 6, если отвергается, управление передается блоку 9.
- Проверяется (блок 6), все ли возможные в данном интервале границы исчерпаны. Если проанализированы не все границы, то управление передается блоку 7, в противном случае - блоку 10.
- Подготовляется (блок 7) для анализа очередная граница, и управление передается блоку 3 (вычисление v).
- Сопоставляются (блок 8) значения критерия v для данной и предыдущей границ. Если для данной границы значения критерия v больше, чем для предыдущей, то осуществляется переход к блоку 9, в противном случае - к блоку 14.
- Запоминается (блок 9) найденное значение критерия v и осуществляется переход к блоку 6.
- Проверяется (блок 10), не было ли сохранено для данной границы значение критерия v, и в зависимости от того, какой ответ получен - утвердительный или отрицательный, управление передается блоку 11 или 12.
- Отбивается данная граница (блок 11) и осуществляется переход к блоку 12.
- Проверяется, все ли интервалы проанализированы (блок 12), и в зависимости от ответа осуществляется переход к блокам 13 или 16.
- Подготовляется (блок 13) для анализа очередной интервал и передается управление блоку 2.
- Отбивается данная граница (блок 14).
- Подготовляется (блок 15) для анализа новый интервал в пределах от выделенной границы до конца исследовавшегося перед этим интервала. Переход к блоку 2. Рассмотренная группа блоков (1-15) реализует первый этап в решении задачи - получение предварительного расчленения. Второй этап (блоки 16-22) предусматривает уточнение (коррекцию) выделенных границ. При таком уточнении, в частности, выбрасываются все заданные вначале фиктивные границы, если только не будет случайного совпадения такой фиктивной границы с границей реальной. Продолжим рассмотрение схемы алгоритма.
- Выбирается первая пара смежных интервалов, I полученных в результате найденного в итоге работы блоков расчленения (блок 16).
- Вычисляется значение критерия v для границы между этими интервалами (блок 17).
- Проверяется гипотеза об однородности интервалов (блок 18).
- Если гипотеза не отвергается, граница, разделяющая эти интервалы, выбрасывается (блок 19).
- Проверяется, все ли интервалы просмотрены (блок 20). Если интервалы не исчерпаны, то подготовляется к анализу новая пара интервалов - второй из ранее анализированных .и следующий за ним. При этом если граница между проанализированными перед этим интервалами была отброшена, то не второй из них, а объединение первого и второго сопоставляется с новым интервалом (блок 21).
- Если же все интервалы исчерпаны, то печатается последовательность выделенных границ (блок 22).
Ниже приведен ряд примеров машинного выделения однородных в том или ином геологическом смысле объектов по алгоритмам, близким к рассмотренном выше.

Рис. 16. Результаты машинного расчленения разреза скважины по кривым изменения микроэлементов (в 10-3 %) в горных породах. 1 - пестроцветные глины; 2 - прослои алевролитов; 3 - темно-серые слюдистые глины; 4-5 - кора выветривания: 4 - глинистая, 5 - гидрослюдистая
На рис. 16 дано полученное В. Я. Воробьевым с помощью ЭЦВМ расчленение разреза одной из скважин, пробуренной в районе Гайского месторождения, но данным распределения микроэлементов в горных породах. Машиной выданы четыре границы, две из которых, характеризующиеся существенно более высокими значениями критерия v, отделяют юрские отложения от отложений других возрастов (от пестроцветных плиоценовых глин и от доюрской коры выветривания). Меньшие значения критерия v соответствуют границам между различными диалогическими разностями одновозрастных отложений. Кора выветривания разделена на две части: верхнюю, глинистую, и нижнюю, гидрослюдистую, а юрские отложения - на нижнюю толщу (темно-серые слюдистые глины) и верхнюю, содержащую прослои алевритов.

Рис. 17. Результаты машинного анализа кривых содержания элементов (в %) в глинах разного возраста
На рис. 17 показан произведенный В. Я. Воробьевым машинный анализ изменения содержания элементов в глинах разного возраста (по материалам А. П. Виноградова). Машиной уверенно выделены отложения перми и триаса, характеризующиеся специфичностью физико-химической обстановки.
На основе машинного расчленения ряда профилей и корреляции произведенных расчленений возможно построение карт. На рис. 18 приведен пример такой карты, полученной В. Я. Воробьевым. На основе машинной обработки четырех геохимических профилей в одном из районов Южного Урала был установлен ряд разностей горных пород: сланцы ордовикского возраста, карбонаты, две разновидности серпентинитов, а также никеленосная кора выветривания.
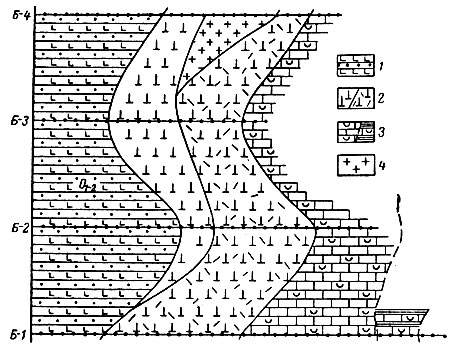
Рис. 18. Геохимическая карта, построенная на основе выделения однородных геологических тел с помощью ЭЦВМ. 1 - сланцы; 2 - серпентиниты; 3 - карбонатные породы; 4 - никеленосная кора выветривания
В области гидрогеологии математические методы и средства вычислительной техники применяются для решения таких задач, как прогноз подпора подземных вод в районах гидротехнического и гидромелиоративного строительства, выбор наиболее рациональных типов защитных дренажей в пределах орошаемых и подтопляемых территорий, на промплощадках и в населенных пунктах, выбор рациональных систем осушения заболоченных земель, выбор рациональных систем осушения месторождений полезных ископаемых, оценка запасов подземных вод и др. При решении этих задач до последнего времени использовались главным образом аналоговые вычислительные устройства, однако сейчас заметен переход к применению ЭЦВМ, особенно для решения трехмерных задач.
* * *
Из приведенного обзора следует, что математизация и кибернетизация в настоящее время коснулись почти всех областей геологии и в особенности поисков и разведки полезных ископаемых. Однако предстоит еще очень большая, сложная и трудная работа. До последнего времени внедрение математических методов и современной техники сдерживалось явной оппозицией со стороны геологов, придерживающихся традиционных методов в геологических исследованиях. Однако не менее опасен и противоположный уклон - чрезмерное увлечение применением вычислительных средств и математического аппарата при решении геологических задач.
В настоящее время работы по алгоритмизации процесса обработки геологической информации продвинулись настолько, что мы уже в состоянии составить алгоритм для любого более или менее четко сформулированного этапа обработки геологических материалов. Однако всегда нужно отличать принципиальную возможность реализации на ЭЦВМ того или иного этапа обработки от экономически эффективной его обработки. Большие ЭЦВМ очень дороги - стоимость нескольких минут работы машины равна стоимости целого рабочего дня квалифицированного работника, поэтому говоря об автоматизации обработки, необходимо тщательно анализировать экономический эффект, который она несет. Поскольку стоимость обработки складывается из стоимостей передачи информации в место обработки, преобразования первичной информации в форму, удобную для ввода в машину, сбора и преобразования дополнительных данных, необходимых для обработки первичной информации, разработки программы для ЭЦВМ, затраченного на обработку машинного времени, оформления полученного результата,- то упущение в процессе автоматизации обработки какого-либо звена может свести на нет ее экономическую эффективность.
Необходима тщательно продуманная работа для того, чтобы огромные возможности, открывающиеся в связи с использованием современной вычислительной техники в геологоразведочных работах, были претворены в действительность.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'