1. Что такое искусственный интеллект?

В области исследований, называемой искусственным интеллектом, изучаются способы создания вычислительных машин, обладающих "интеллектуальным" поведением. Чтобы лучше понять сущность таких исследований, необходимо прежде всего разобраться в смысле самого понятия интеллект и вытекающего отсюда понятия интеллектуального поведения. Необходимо сказать и о том, что может подразумеваться под словом машина в современном понимании, хотя этот вопрос несравненно более простой, чем попытка определить интеллект. По существу, последний так и не получил достаточно удовлетворительного объективного определения. Поэтому, хотя мы еще коснемся в дальнейшем данного вопроса, в конечном счете нам придется вернуться к нашему интуитивному представлению об интеллекте, но дополненному и расширенному на основании результатов тех исследований, которые по сложившейся традиции принято относить к области искусственного интеллекта.

В данном контексте слово машина обычно означает некоторую программу, реализуемую на универсальной вычислительной машине. В некоторых случаях строились электронные устройства специального назначения, но по своей сущности они аналогичны вычислительным машинам. Такие "машины" по своим свойствам и виду совершенно не похожи на грубые и мощные машины, характерные для первой промышленной революции. Однако в последние годы наблюдается определенная тенденция, направленная на создание все более сильных ("мускулистых") машин искусственного интеллекта. В одном из разделов искусственного интеллекта, называемом роботикой, рассматриваются вопросы использования интеллектуальных машин для манипулирования предметами в реальном мире.

Что такое интеллект?

Психологи обычно с большой осторожностью подходят к вопросу об определении понятия интеллекта. Как заметил один из них, единственное непротиворечивое определение состоит в следующем: "Интеллект - это то, что оценивается в интеллектуальных тестах". Некоторые исследователи, работающие в области искусственного интеллекта, пошли именно по этому пути, составив программы для решения задач типа тех, которые предлагаются в тестах по проверке уровня интеллектуальности.

Однако предпочтительнее было бы иметь более общее определение. Интеллект иногда определяют как способность правильно реагировать на новую ситуацию. С таким определением хорошо согласуются и результаты некоторых экспериментов по оценке "уровня интеллектуальности" животных. Предположим, что обезьяна находится в комнате, где с потолка свисает гроздь бананов; однако они расположены слишком высоко, чтобы обезьяна могла их достать с пола. Но в комнате имеется коробка, подставив которую под бананы и взобравшись на нее, обезьяна могла бы дотянуться до лакомства. Если обезьяна действительно проделывает эту операцию и срывает гроздь бананов, то тем самым она проявляет способность думать, т. е. интеллект. Перед обезьяной ставили и более сложную задачу: используя палку или соединяя две палки вместе, она должна была "выудить" фрукты с большого расстояния.

Тип "интеллекта", проявляющийся в подобных опытах, близок к нашему интуитивному определению этого понятия, однако такое определение не вполне объективно. Чтобы установить, что данная ситуация является "новой" в точном смысле слова, необходимо субъективное суждение. Например, перед карманным калькулятором поставлена задача перемножить два числа; если эти числа велики и не относятся к хорошо известным числам типа приближенного значения числа "пи" или числа дюймов в миле, то вполне возможно, что такая задача будет совершенно новой для калькулятора, ибо он никогда прежде не сталкивался с перемножением таких чисел. Тем не менее нам обычно не приходит в голову считать его "разумным" на том основании, что он правильно реагирует в новой ситуации. "Новизна" этой ситуации совсем иная, чем в случае обезьяны и бананов, но это отличие трудно сформулировать точно.

Попытка определить понятие "интеллект" равносильна попытке дать определение мышлению при ответе на вопрос "могут ли машины мыслить?". Можно сказать, что сама проблема искусственного интеллекта и есть не что иное, как попытка ответить на этот вопрос. То обстоятельство, что сегодня мы вряд ли могли бы рассматривать микрокалькулятор как "интеллектуальное" или "мыслящее" устройство, свидетельствует именно о том, что любая попытка создать интеллектуальную или думающую машину автоматически подразумевает самоотрицание. Сам факт, что машина обладает некоторым типом поведения, заставляет людей говорить: "Это не то, что мы подразумеваем под мышлением, ибо мы понимаем, как машина может это делать". Пока разработка искусственного интеллекта не достигнет своей высшей цели - дублирования каждого аспекта человеческого интеллекта (что, по-видимому, неосуществимо в обозримом будущем), ему обязательно будет присуще такое самоотрицание. Как обречена на провал попытка человека дойти до места, где "начинается" радуга, так и маловероятно достижение этой цели при создании искусственного интеллекта. Впрочем, поиски будут небесплодны - они обогатят нас новыми знаниями. Несколько поколений назад люди, несомненно, сочли бы карманный калькулятор "интеллектуальным", а сегодня для такой оценки от машины требуется гораздо большее.

Поэтому искусственный интеллект - это область исследований, направленных на то, чтобы заставить машины выполнять функции, которые в настоящее время для них слишком трудны, и особенно такие функции, которые способны выполнять люди. Слова "в настоящее время... трудны" говорят о том, что подобное определение должно быть "скользящим", т. е. меняться со временем, точно так же как изменяется наше представление о "думающей машине" по мере развития техники. Поскольку эта проблема искусственного интеллекта, по существу, беспредельна и она привлекла к себе многих способных людей, ее по праву считают "передним краем" разработок в области вычислительной техники. Более подробно мы будем говорить об этом в гл. 13.

Представляет интерес тест, позволяющий сказать, является ли машина "думающей", который предложил известный математик и специалист в области вычислительной техники Алан Тьюринг [1]. Этот тест основан на "игре в переговоры". Тьюринг, должно быть, не раз бывал на довольно скучных вечеринках, где гостей развлекают играми такого рода: кто-то из компании незаметно уходит в другую комнату, а другим гостям предлагают задавать вопросы отсутствующему с тем, чтобы из ответов выяснить, мужчина это или женщина. Разумеется, отсутствующий отвечает не непосредственно, а либо в письменной форме, либо через посредника.

Идея Тьюринга состояла в том, чтобы посредством подобных переговоров испытывать машину на "интеллект". Если лицо, задающее вопросы, не в состоянии установить, общается он с человеком или с машиной, и если на самом деле это была машина, то следует считать, что машина обладает "интеллектом".

Можно сказать, что существующие ныне программы для вычислительных машин вполне удовлетворяют тесту Тьюринга в его простом варианте. Отдельные игровые программы (гл. 5 и 6) достаточно хорошо имитируют поведение человека, так что некоторые люди уверены, что они играют с человеком. Хорошо известна программа ЭЛИЗА, играющая роль психиатра. Пациенты, с которыми "беседовала" эта программа, в большинстве случаев не сомневались в том, что они общаются с врачом.

Такие программы, однако, не имитируют полностью интеллект человека, способного вести разговор на самые различные темы, - а именно это, по-видимому, имел в виду Тьюринг. Очевидно, что игровые программы соответствуют поведению людей лишь в весьма ограниченной области. Программа ЭЛИЗА моделирует поведение осторожного психиатра, который сообщает больному самую ничтожную информацию (как нередко поступают и настоящие психиатры).

Вычислительные машины могут весьма эффективно имитировать поведение человека в какой-нибудь узкой области деятельности. Тот факт, что иногда сами люди стараются определенным образом ограничить свои действия, делает тест Тьюринга неточным. Этот тест может показаться неудовлетворительным и потому, что Тьюринг рассматривает вопрос лишь о моделировании интеллекта, а не задачу достижения какого-то полезного (или потенциально полезного) результата (см., однако, заключительные замечания к гл. 15).

Возможен ли искусственный интеллект?

Теперь читатель, видимо, убежден, что за словами искусственный интеллект стоит важное научное направление, - и это действительно так. Проблема искусственного интеллекта выделяется среди всех других работ в области вычислительной техники и программирования. Тем не менее остаются открытыми два важных вопроса:

а. Действительно ли методы, которые объединены в понятии искусственный интеллект, имитируют в значительной мере то, что мы интуитивно понимаем под интеллектом? Другими словами, оправдан ли сам термин искусственный интеллект?

б. Существуют ли такие аспекты интеллекта человека, которые в принципе нельзя смоделировать на вычислительной машине?

Первый из этих вопросов весьма близок к ранее поставленному вопросу: могут ли машины мыслить? Оба эти вопроса весьма неточны и во многом зависят от нашего интуитивного представления об интеллекте, а также от целого ряда других, столь же нечетких понятий. Вследствие нечеткости самого вопроса при его рассмотрении нам необходимо сразу же отказаться от тенденции не считать тот или иной вид деятельности проявлением интеллекта только на том основании, что он осуществляется машиной.

В конкретных задачах, таких, как игра в шахматы, деятельность человека и машины поддается сравнению. Многие, и прежде всего Г. Дрейфус, высказывали соображения, что существуют целые области деятельности человека, в которых машина не может даже и близко подойти к имитации человека. Нам же, пожалуй, лучше всего вообще отказаться от сопоставлений такого рода до тех пор, пока мы не подведем итог результатам, достигнутым в исследованиях по искусственному интеллекту (гл. 13 и 14).

Имеется, однако, один вопрос, который небесполезно будет рассмотреть сейчас, а именно: способны ли машины к "новаторству"? Хотя некоторые черты "искусственного интеллекта" мы можем обнаружить в системах, созданных во времена, предшествующие эре ЭВМ (например, в автоматах, играющих в шахматы), сегодняшние исследования в области искусственного интеллекта почти полностью опираются на ЭВМ. И это неудивительно, поскольку ЭВМ по сравнению с другими искусственными системами во многих важных аспектах наиболее близки мозгу по своему действию. Из всех искусственно созданных устройств они самые сложные. С мозгом их роднит также и степень универсальности, вследствие чего весьма трудно сколько-нибудь определенно судить об их возможностях.

Высказывается, однако, мысль, что вычислительные машины обречены быть "глупыми". Все, что они в состоянии делать, так это следовать шагам, указанным в программе, подготовленной для них программистом-человеком. Безусловно, программист имеет возможность заложить в программу "точки выбора", когда последующие операции машина должна избирать из двух или более возможных вариантов в зависимости от результатов предыдущих вычислений. Тем не менее общее соображение остается тем же: вычислительная машина слепо выполняет последовательность операций, заранее намеченных программистом. Кажется невозможным, чтобы столь "глупое" устройство когда-либо удалось наделить "интеллектом". Обычно предполагается, что с последним связана способность "создания нового" (а это свойство также весьма трудно сформулировать точно). Предположение же, что программируемое устройство способно привносить что-то новое, противоречиво по самой своей сути.

Компьютеры всегда рассматривались как бы с двух различных сторон, что отражено в весьма эксцентричном определении "умно-глупые", предложенном для них Хофштадтером [2]. Когда появились первые цифровые вычислительные машины, в популярной литературе их называли "гигантским мозгом". Достаточно ответственные ученые сочли тогда необходимым выдвинуть более трезвую точку зрения, подчеркивая роль машины как послушного исполнителя воли человека. Однако несколько лет спустя, когда вычислительные машины и методы программирования достигли значительного совершенства, многие из этих ученых изменили свою точку зрения.

Нельзя уйти от того факта, что вычислительная машина действительно является послушным исполнителем программы. Но когда ЭВМ и программа становятся достаточно сложными, поведение машины может оказаться практически непредсказуемым (хотя оно и предсказуемо в принципе). Поэтому не лишено смысла рассматривать машину как устройство, потенциально способное к "новаторству". Если нет более простого способа предсказывать поведение машины, чем только наблюдать за ее работой (или другого способа, сравнимого по сложности), то предсказуемость ее поведения в некотором отношении теряет смысл. В действительности работу человеческого мозга можно было бы считать "предсказуемой" (если пренебречь эффектами случайных шумов, см. далее). Возможно, если бы мы знали характеристики каждого нейрона (нервной клетки) мозга, схему их взаимосвязи и степень их возбуждения в какой-то момент времени, то поведение мозга можно было бы предсказывать. Поэтому предсказуемость поведения вычислительных устройств сама по себе не исключает наличия у них "интеллекта" и способности к созданию нового.

Слово "предсказуемый" мы использовали здесь несколько вольно: при этом неявно предполагалось, что входные сигналы, поступающие в машину или мозг, могут быть предсказаны (возможно, на основе предшествующих выходных сигналов). Для описания систем, предсказуемых в этом смысле, разработаны формальные приемы. Если машина имеет конечный объем памяти, то ее можно описать как конечный автомат; если же объем памяти неограничен, то это должно быть устройство, эквивалентное машине Тьюринга. Программа для вычислительной машины - почти по определению - является конечным автоматом (см. Приложение 1 к настоящей главе).

Конечные автоматы и машины Тьюринга являются детерминированными системами - в них отсутствуют непредсказуемые воздействия типа случайных помех. Согласно некоторым данным, случайные помехи оказывают влияние на работу мозга. Порог возбуждения нейрона, очевидно, подвержен случайным флуктуациям; предполагается также, что нейроны мозга, по-видимому, совершенно случайным образом умирают, не получая никакой замены. (По оценкам Д. Бернса, в мозге взрослого человека ежедневно умирает около ста тысяч нервных клеток.) Искусственные системы также могут испытывать воздействие случайных шумов, так что нельзя считать, что это свойство само по себе отличает мозг от машины. Однако в действительности мозг в этом отношении отличается от большинства программ для ЭВМ, поскольку их составляют так, чтобы они были детерминированными, т. е. не подверженными случайным воздействиям.

В старых моделях вычислительных машин детерминированность их работы пытались обходить, используя естественные источники случайных чисел, которыми служили такие непредсказуемые процессы, как шум резистора или радиоактивный распад. При этом действия машины носили детерминированный характер, за исключением тех случаев, когда в программу включалась инструкция специального типа для выработки случайного числа.

В современных вычислительных машинах такие источники случайных чисел не применяются. Для вычислительных задач, в которых требуется создание последовательностей чисел, подобных случайным, они обычно генерируются с помощью специальных процедур. Поэтому такие числа называют "псевдослучайными", ибо они формируются из одной и той же циклической последовательности. Процесс генерирования псевдослучайных чисел, по существу, является чрезвычайно компактным способом хранения очень длинной (циклической) таблицы случайных чисел. Поскольку этот цикл весьма длинный, последовательность чисел, используемых программой, представляет собой малую долю всего цикла; а так как последовательность можно начинать с различных точек цикла, это позволяет получать огромное разнообразие последовательностей. Иногда делают так, что начальная точка последовательности определяется показаниями часов "действительного времени", указывающих время дня (и, возможно, дату) в тот момент, когда требуется построить первое число в последовательности. Это удобный способ, дающий возможность с каждым запуском программы получать различные последовательности, как это было бы и в случае использования естественного источника случайных чисел.

В приложении 2 к настоящей главе мы рассказываем о способах получения псевдослучайных чисел. На самом деле случайные (или псевдослучайные) числа не являются неотъемлемой частью программ, характерных для основного направления исследований по искусственному интеллекту, но они весьма важны в программах (гл. 14), способных создавать свои собственные эвристики.

К генератору случайных или псевдослучайных чисел часто прибегают при разработке программ, воплощающих "кибернетический" подход к искусственному интеллекту. Такой подход необходим, например, при реализации как "слияния", так и "деления с мутацией", постулируемых Селфриджем в его пандемониуме (гл. 7); он требуется также для персептронов, особенно в варианте Робертса (гл. 8). Этот подход используется во всех методиках создания машинных "произведений искусства" (гл. 11) и служит надежным инструментом для программистов.

Как видим, существуют разнообразные подходы к искусственному интеллекту, и нам следует обсудить взаимосвязь между ними и отношение каждого из этих подходов к кибернетике.

Кибернетика и искусственный интеллект

Некоторые специалисты, по существу, отождествляют кибернетику с работами в области искусственного интеллекта, Такая точка зрения согласуется с определением кибернетики, которое приводится как подзаголовок к книге Винера [3], а именно: "Управление и связь в животном и машине". Нет сомнений, что упоминание живого организма существенно, ибо главная цель исследований в области кибернетики - более глубокое понимание процессов, происходящих в живых организмах и сообществах живых организмов.

Из всех этих процессов наибольший интерес представляет работа мозга (что, разумеется, не означает отсутствия нерешенных задач, относящихся к системам более низкого уровня).

При изучении сущности и, следовательно, истоков кибернетики целесообразно обратиться к другому из пионеров в этой области исследований - Уоррену Маккалоку. Хотя именно Винер предложил название "кибернетика" и определил в своей книге ее формальный статус, многие из активно работавших в то время ученых считали, что Маккалок, по крайней мере в равной степени, заслуживает титул "отца кибернетики". (Во времена формального зарождения кибернетики эти два крупных мыслителя были друзьями, и поэтому довольно сложно определить по отдельности вклад каждого из них. Причины же раскола, происшедшего между ними несколькими годами позже, до сих пор остаются совершенно неясными.)

Маккалок [4] связывал развитие кибернетики с собственными попытками ответить на вопрос, который он сформулировал так: "Что же такое число, которое человек способен понять, и что же такое человек, способный понять число?" Рассмотрение этого вопроса, очевидно, приводит к проблеме искусственного интеллекта и поднимает проблемы эпистемологии (теории познания), т. е. отражения окружающего мира в нервной системе или машине. Маккалок считал, что такая эпистемология должна быть "экспериментальной"; он искал решения проблемы, исследуя различные экспериментально наблюдаемые свойства нервной системы вплоть до отдельных нервных клеток.

Итак, казалось бы, позиция тех, кто отождествляет кибернетику с проблемой искусственного интеллекта, по существу, верна; однако многие исследователи, работающие в этих двух областях, не считают их тождественными. Безусловно, большинство исследователей, связанных с основным направлением работ в области искусственного интеллекта, будут отрицать, что они занимаются кибернетикой. Специалисты по кибернетике более широко рассматривают свою дисциплину, и поэтому они склонны считать искусственный интеллект лишь разделом кибернетики. Тот факт, что эти две области исследований не воспринимаются как эквивалентные, с очевидностью подчеркивается и выбором тем для книг, которые публикуются в нашей серии: если бы искусственный интеллект и кибернетика были, в сущности, синонимичными понятиями, то вряд ли было бы целесообразно одну из книг серии целиком посвятить проблеме искусственного интеллекта.

Как отмечалось ранее, существует некоторое разнообразие в подходах к проблеме искусственного интеллекта, но, вероятно, правильнее говорить о некой дихотомии, поскольку эти подходы можно разделить на два главных направления. То, что сейчас обычно понимают под исследованием в области искусственного интеллекта (и что мы назвали здесь "основным направлением" в этой области), - это работа, абсолютно свободная от каких-либо попыток моделирования процессов активности нервной системы. Большинство программ, созданных для вычислительных машин (эта работа ведется исключительно с применением ЭВМ), не предусматривают возможности обучения "на опыте". Про эти программы можно лишь сказать, что если они вообще моделируют мыслительную деятельность человека, то на достаточно высоком уровне. Но это, конечно, не исключает их потенциальной ценности для познания механизма действия мозга: систему такой сложности, какую представляет собой мозг, необходимо исследовать самыми различными методами, включая - возможно, в первую очередь - моделирование высоких уровней.

В первые годы развития кибернетики - примерно до 1958 г. - подобная дихотомия в подходах к исследованиям не была очевидной. Специалисты по искусственному интеллекту (в смысле современного "основного направления") считают, что начало их деятельности было положено публикациями примерно этого периода (которые, естественно, касались работ, осуществленных несколько ранее). Марвин Минский и Джон Маккарти были пионерами, подготовившими почву для будущих исследований, причем Маккарти явился создателем языка программирования ЛИСП (гл. 13). Минский был связан с Массачусетским технологическим институтом (США) и, основываясь на идеях Маккалока, развивал отмеченную дихотомию в подходах к проблеме. Важными исследованиями занимались в то время Ньюэлл, Шоу и Саймон (гл. 3), работавшие над созданием "универсального решателя задач", Сэмюэль (гл. 6), Селфридж (гл. 7) и некоторые другие.

Дихотомия подходов к проблеме создания искусственного интеллекта отражена и в заголовке учебника Слейгла [7]: "Искусственный интеллект - подход на основе эвристического программирования". Этот автор в действительности занимается тем, что мы определили здесь как "основное направление", на которое (за неимением подходящего термина) он указывает в развернутой форме данным подзаголовком. И этот подзаголовок вполне уместен, поскольку эвристики широко используются в работах, ведущихся в рамках названного подхода.

Дихотомия подходов также отмечается и анализируется в предисловии к хорошо известной книге Фейгенбаума и Фельдмана [8], которая в период ее публикации (1963) была признана лучшим сборником наиболее значительных статей по проблеме искусственного интеллекта. Для обозначения "основного направления", или "эвристического программирования", авторы используют не вполне ясный термин "модели понимания", противопоставляя этот подход другому подходу к созданию искусственного интеллекта, а именно "нейронной кибернетике", или "самоорганизующимся системам". По этому поводу они дают следующий комментарий:

Специалисты по нейронной кибернетике подходят к проблеме разработки интеллектуальных машин, постулируя существование большого числа очень простых элементов обработки информации, собранных в случайную или организованную сеть, и наличие некоторых процессов стимулирования или подавления их активности. Создатели моделей понимания отличаются более "макроскопическим" подходом и основываются в своих работах на в высшей степени сложных механизмах переработки информации. Они полагают, что создание интеллектуальной машины - задача настолько трудная, что ее невозможно решить, не начав все с самого начала, и поэтому включают в свои системы процессы обработки информации той максимальной степени сложности, которую только они способны сами понять и передать вычислительной машине (путем программирования).

Затем Фейгенбаум и Фельдман переходят к сравнению результатов, достигнутых в рамках каждого из подходов, и делают вывод, что в области "моделей понимания" успехи несравненно значительнее. Они заявляют фактически, что прогресс (на 1963 г.) в "нейронной кибернетике" едва заметен. Анализируя сети простейших элементов обработки информации, они говорят о многочисленных попытках создания "самоорганизующихся систем", которые должны были бы научиться интеллектуальному поведению в процессе взаимодействия с окружающим миром. Целью этих исследований является моделирование способностей нервной системы к самоорганизации и самообучению, и поэтому обычно компоненты систем конструируются так, чтобы их параметры имели некоторое сходство с известными свойствами нервных клеток.

Нет необходимости говорить, что споры между сторонниками двух отмеченных подходов к проблеме искусственного интеллекта продолжаются и поныне. Большая часть настоящей книги посвящена описанию работ, ведущихся в рамках "эвристического программирования", или "моделей понимания"; это объясняется тем, что, как и в 1963 г., в данной области имеется гораздо больше успехов, о которых можно было бы говорить. Однако мы будем настаивать на необходимости иного подхода. Подход с позиций эвристического программирования открыт для критики, поскольку это метод ad hoc (на данный случай), когда в контексте различных задач предлагаются и различные типы решений. Обсуждение этих общих аспектов проблемы мы отложим до заключительных глав, а прежде рассмотрим уже достигнутые результаты.

Теперь же следует остановиться - быть может, с некоторым опозданием - на целях, которые преследует работа в области искусственного интеллекта.

Цели создания искусственного интеллекта

Попытка заставить машины действовать как можно более "разумно" (что бы под этим ни подразумевалось) привлекательна сама по себе, и создается впечатление, что многие исследователи, работающие в этой области, не делали серьезных попыток мотивировать свою деятельность. Как и во многих других областях научных исследований, Мотивации деятельности можно разделить на две группы: объяснение и использование.

Некоторые работы по искусственному интеллекту были начаты с заявления, что цель этих работ заключается в выяснении процессов, связанных с мышлением человека, путем их моделирования в программах для вычислительной машины. Некоторые энтузиасты даже утверждали, что ни один истинный психолог не приступит к работе без создания такого рода моделей. Исследования Ньюэлла, Шоу и Саймона по созданию универсального решателя задач были направлены на моделирование поведения испытуемых, решающих те или иные задачи. Испытуемые должны были рассказывать возможно более подробно о том, как они ищут решение, и весь ход их рассуждений записывался на магнитофон. В дальнейшем была создана программа GPS^*, моделирующая содержание "протоколов", которые вели испытуемые. Разумеется, точность такого моделирования зависит от того, в какой степени процесс решения проблемы поддается анализу и в какой степени его можно описать словами. Однако об этом мы расскажем позже.

^* (GPS (General Problem Solver) - универсальный решатель задач. - Прим. перев.)

Даже в том случае, когда создание программы не является откровенной попыткой смоделировать экспериментально наблюдаемое поведение человека, сама поставленная цель - построить "интеллект" - предполагает моделирование действий человека на некотором уровне, а следовательно, и возможность более глубокого понимания естественного интеллекта.

В некоторых программах искусственного интеллекта используются принципы, явно не соответствующие способам, к которым прибегает человек для достижения подобного результата. Например, все существующие хорошие программы для игры в шахматы, по общему мнению, не копируют методов анализа партии, которым пользуются шахматисты (гл. 5). Но даже в этом случае изучение методов решения проблем, необходимое для создания программы, может косвенным образом углубить наше понимание методов, к которым прибегает человек. Такое изучение в какой-то мере развивает интуицию, касающуюся природы рассматриваемой задачи, и дает возможность выдвигать кое-какие гипотезы относительно методов, которые могли бы использоваться шахматистами-людьми. (Подобные соображения следует высказывать, однако, с большой осторожностью: любое утверждение о масштабах или характере проблемы неизбежно связано с имеющимися в нашем распоряжении методами, однако в ходе естественной эволюции, без сомнения, возникли какие-то "хитрости", которые еще не пришли в голову программистам.)

Разделы проблемы искусственного интеллекта

В этой главе (и в оглавлении к настоящей книге) мы упоминали различные разделы, которые выделяются в проблеме искусственного интеллекта. Работы в области искусственного интеллекта ведутся в следующих основных направлениях:

Доказательство теорем. Оно перекрывается с определенными областями математики и решением проблем в ряде других областей (например, в роботике).

Модели игр. Особое внимание уделяется шахматам.

Распознавание образов. Эта проблема касается распознавания зрительных или слуховых образов, а также образов других (смешанных) модальностей. Медицинская диагностика и предсказание погоды являются примерами задач распознавания образов, не связанных с какой-то конкретной модальностью. В последнее время большая часть работ в этой области ориентирована на анализ сцен, а не на распознавание отдельных объектов (например, печатных знаков), что важно для роботики.

Использование естественного языка. Большое внимание уделялось системам вопрос-ответ и системам автоматического перевода. Последняя работа Винограда связала естественный язык с роботикой.

Роботика. Эта область имеет непосредственную практическую ценность.

Экспертные системы. В них воплощаются большие объемы знаний и навыков, присущих эксперту-человеку. Эти системы представляют большую ценность в медицинской диагностике и в некоторых других областях.

Инженерия знаний. Эта область не является самостоятельной, но сам термин отражает определенное отношение к тому, каким образом следует осуществлять взаимодействие различных видов знаний в распознавании образов, роботике и в экспертных системах^*.

^* (Здесь автор не совсем прав. Английский термин Knowledge Engineering включает и ту область, в рамках которой ведутся исследования по представлению знаний, манипулированию ими и слежению за пополнением и корректировкой знаний. - Прим. ред.)

Приложение 1. Конечные автоматы

Автомат считается конечным, если он может находиться в любом из некоторого конечного множества состояний. Если, кроме того, имеется конечное множество входных сигналов, а также конечное множество выходных сигналов и автомат является детерминированным, то он может быть задан перечислением для каждого из состояний результирующих эффектов, создаваемых каждым из входных сигналов. Эти эффекты могут носить двоякий характер: во-первых, они приводят к появлению некоторого выходного сигнала и, во-вторых, обычно вызывают изменения состояния автомата.

Таким образом, автомат [9] определяется пятью компонентами. Первые три - это списки множеств состояний, входных и выходных сигналов. Остальные два компонента - это отображения декартова произведения состояний и входов на множество состояний и на множество выходов.

Предположим, что на вход автомата поступают одиночные двоичные сигналы (0 или 1) и что на выходе он выдает единичный сигнал каждый раз, когда получает подряд три единичных сигнала, не перемежающихся с нулевыми сигналами. После того как на выходе выдается единица, счетчик входных сигналов возвращается к нулю, и для того чтобы на выходе вновь появился единичный сигнал, на вход должно поступать три единичных сигнала подряд. Для подобного поведения автомат должен иметь четыре состояния, соответствующие 0, 1, 2 или 3 входным единичным сигналам, поступающим подряд.

Отображение декартова произведения в некоторое множество можно представить таблицей. Ее элементы соответствуют каждой паре состояние - вход. Отображение, показывающее следующее состояние автомата, который мы описали, имеет следующий вид:

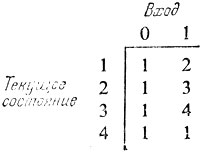
В качестве начального состояния автомата служит состояние 1.

Отображение, определяющее выход, имеет вид

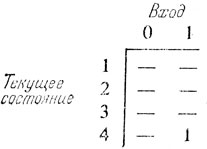
где черточка означает отсутствие выходного сигнала.

Хотя вычислительная программа, по существу, представляет собой конечный автомат, обычно ее редко описывают подобным образом. Число состояний у такого автомата, как правило, чрезвычайно велико, так как новое состояние возникает всякий раз, когда изменяется один двоичный разряд в одном из "слов" вычислительной машины, в которых хранятся данные. (В гл. 2, рассматривая вопрос о комбинаторном взрыве, мы кратко, остановимся на представлении о больших числах.)

При исследовании некоторых вопросов, касающихся того, что можно и что нельзя вычислить, оказалось полезным рассмотреть специальный тип вычислительной машины, называемой машиной Тьюринга. На практике вычислительные машины не строятся по принципу машины Тьюринга, однако, по-видимому, все, что можно вычислить на машине Тьюринга, можно вычислить и на любой другой вычислительной машине с достаточными размерами памяти, и наоборот. Поскольку представление о машине Тьюринга неразрывно связано с теоретическим анализом, удобно отождествлять "вычислимость" вообще с "вычислимостью" на машине Тьюринга.

Машина Тьюринга содержит конечный автомат, но число состояний, которое он должен иметь, существенно уменьшается вследствие того, что информация хранится вне автомата. Предполагается, что этот автомат соединен с читающей и пишущей головкой, которая может записывать символы на ленте и считывать их. Символы, считываемые с ленты, становятся входными сигналами для конечного автомата. Каждый выходной сигнал автомата представляет собой комбинацию из символа, который предстоит поместить на ленту в текущем положении читающе-пишущей головки, и инструкции о продвижении ленты вперед или назад на определенное число позиций.

Обеспечиваемое лентой хранение информации вне автомата позволяет значительно упростить конструкцию автомата по сравнению с той, которая потребовалась бы для выполнения тех же самых операций в отсутствие ленты. Это также означает, что машина Тьюринга не ограничена никаким фиксированным объемом памяти, поскольку предполагается, что лента бесконечна. Отделение данных (хранимых на ленте) от программы и средств ее выполнения (предоставляемых конечным автоматом) хорошо соответствует обычному представлению о процессе вычисления. На практике же вычислительные машины не располагают неограниченной памятью, но память современных вычислительных машин очень велика. Поскольку машина Тьюринга - это теоретическая конструкция, помогающая выяснить, что вычислимо в принципе, целесообразно считать, что она располагает бесконечной памятью.

Чтобы понять, как работает машина Тьюринга, предположим, что на ленте в каждой позиции может находиться один двоичный разряд (например, 0 или 1). Предположим далее, что число n (положительное целое) представляется на ленте в виде последовательности из n единичных разрядов, ограниченной в начале и в конце нулевыми разрядами. Тогда машину Тьюринга, предназначенную для вычитания единицы, можно построить следующим образом. Допустим, что читающе-пишущая головка первоначально находится над самым левым единичным разрядом последовательности (хотя в нашей задаче это может быть любой единичный разряд).

Автомат может заставить головку двигаться вправо (удобнее говорить о движении головки, а не ленты), пока она не встретит нулевой разряд. Тогда она должна отступить на один шаг назад и записать нулевой разряд, стерев тем самым один из единичных разрядов. Автомат должен иметь два состояния. Состояние 1 - это то состояние, с которого автомат начинает и в котором он остается, когда головка перемещается вправо и встречается со следующим единичным разрядом. Состояние 2 возникает тогда, когда, перемещаясь вправо, головка попадает в позицию, соответствующую нулевому разряду. После того как сделан шаг назад и записан нулевой разряд там, где раньше был записан единичный, новое состояние не указывается, а вместо него появляется команда О, означающая "остановка".

Переходы состояний конечного автомата определяются отображением

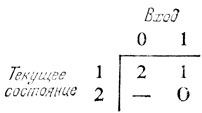
Выходами автомата являются комбинации из двух символов. Первый из них - это символ, который должен быть записан на ленте (он соответствует тому символу, который уже записан на ленте в случае первой строки таблицы), а второй указывает на движение головки влево или вправо. Нижний левый элемент никогда не достигается, а у нижнего правого элемента нет указания относительно движения, поскольку автомат останавливается:

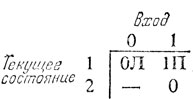
Разумеется, это очень простой пример вычисления, выполняемого машиной Тьюринга.

Теоретическое исследование вопроса вычислимости, ставшее возможным благодаря представлению о машине Тьюринга в случае вычислительного процесса (или в других аналогичных случаях), очень важно для проблемы искусственного интеллекта, так как оно показывает, что некоторые проблемы, анализируемые в области искусственного интеллекта с помощью эвристических методов (см. следующую главу), не имеют алгоритмического решения. В любом случае интуитивно большинство людей и не ожидают алгоритмического решения, тем не менее весьма ценно, когда этот вопрос решен окончательно.

Представление программ как конечных автоматов или как машин Тьюринга, конечно, является абсолютно формальным. В нем не упоминаются такие вещи, как "цель", "обучение" или "стратегия". Далее в этой книге мы будем в основном обсуждать программы в неформальных представлениях, связанных с целенаправленностью работы системы. Однако при этом важно помнить, что возможно совершенно иное представление системы и что исход любой попытки понять, как работает естественный интеллект, зависит от способов представления связанных с ним процессов; причем каждый исследователь выбирает тот способ, который кажется ему наиболее подходящим, но ни один из них нельзя считать универсальным.

Приложение 2. Генераторы псевдослучайных чисел

Генератор псевдослучайных чисел (г. п. с. ч.) предназначен для создания последовательности чисел, имеющей вид случайной и действительно обладающей некоторыми характеристиками случайного процесса. Во всех основных методах генерации случайных чисел сначала формируется последовательность из целых чисел, которые затем можно легко нормализовать так, чтобы на выходе получалась последовательность дробных величин, скажем в интервале от нуля до единицы. При работе г. п. с. ч. каждое целое число вычисляется исходя из предшествующего ему числа (в некоторых схемах исходя из двух или более чисел, непосредственно ему предшествующих).

Пожалуй, наиболее известен метод генерации случайных чисел, первоначально предложенный фон Нейманом. Предположим, что каждое целое число в последовательности содержит до 4r разрядов, где r - целое число. Обычно это двоичные разряды, однако основание исчисления здесь несущественно. В названном методе каждое целое число получается из предшествующего отбрасыванием r последних наименее значащих цифр, а также r наиболее значащих разрядов и возведением в квадрат 2r-разрядного оставшегося числа, что дает новое 4r-разрядное результирующее число.

Такой метод возведения середины числа в квадрат сегодня не используется, поскольку длина цикла генерируемой последовательности зависит от ее начального числа и может оказаться весьма короткой. И действительно, существуют числа, которые при такой процедуре возведения середины числа в квадрат повторяют самих себя. Например, в случае 4-разрядного десятичного числа 2500 при отбрасывании левой и правой цифр получаем 50, что при возведении в квадрат снова дает 2500. Однако при других начальных значениях могут получаться достаточно длинные последовательности и сам метод дает некоторое представление о том, как следует "выдергивать" числа из последовательности, чтобы добиться видимой непредсказуемости.

Наиболее распространены г. п. с. ч., в которых используются мультипликативные процедуры. Каждое число представляет собой предыдущее число, умноженное на некоторую константу. Это должно было бы привести к последовательности все возрастающих чисел, если бы умножение не производилось с использованием операции взятия модуля. Иными словами, новое число является не полным результатом умножения, а лишь остатком, который образуется после деления полного результата на некое фиксированное число, называемое модулем. Если u₁, u₂, ... - последовательные числа в цепочке, то данный метод можно записать следующим образом:

где k - множитель, а М - модуль.

По-видимому, наиболее широко применяется такой мультипликативный г. п. с. ч., в котором [10]

При этом в генерируемом цикле возникают все числа, удовлетворяющие указанному ограничению на u_n, так что любое число в этом интервале может служить начальной точкой. Длина цикла, следовательно, равна 2³¹ - 2, т. е. несколько больше двух миллиардов чисел.

Если генерируемые числа хранятся в двоичной записи, то в указанном методе их длина должна быть равна по крайней мере 31 разряду. Это не всегда удобно в вычислительных машинах с такой короткой длиной слова, как 24 разряда. Тогда 31-разрядное число можно записать в виде двух машинных слов, однако предпочтительнее метод, позволяющий работать с одним словом. В распространенном варианте описанного мультипликативного метода [11] М представляет собой степень двух, скажем 2^h, a k - любая нечетная степень пяти, такая, что k < М. Начальное число должно быть нечетным, и генерируются только нечетные числа. Длина цикла равна 2^h-2. Число нечетных чисел, меньших М, равно 2^h-1, причем они распадаются на два отдельных цикла, каждый длиной 2^h-2.

Обычно при длине машинного слова 24 разряда значение h равно 23 или 24, что дает длину цикла в несколько миллионов. Поясним этот метод, положив h = 4, так что М = 16 и k = 5 (единственная степень 5 и отсюда единственная нечетная степень 5, меньшая чем 16). Если начальное значение равно 3, то последовательность имеет вид

причем предполагаемая длина цикла равна 2^h-2 = 4.

Иногда г. п. с. ч. работает в соответствии с так называемыми m-последовательностями. Последние могут создаваться регистром сдвига с обратными связями [12] (но для удобства вычислений в цифровой вычислительной машине они представляются несколько иначе). На рис. 1 показан регистр сдвига с обратной связью.

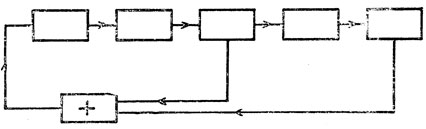
Рис. 1. Пятиразрядный двоичный регистр сдвига с обратными связями от разрядов 3 и 5. Блок со знаком 'плюс' представляет собой сложение по модулю 2

В каждой ячейке регистра содержится двоичный разряд, и в ответ на сдвиговый импульс, поступающий на все разряды, они перемещаются со своего места вправо. Входной сигнал поступает на самую левую ячейку, а его значение в случае регистра сдвига с обратной связью вычисляется исходя из информации, содержащейся в ячейках перед сдвигом. На рис. 1 на вход поступает сумма по модулю 2 содержимого третьей и пятой ячеек. При соответствующем выборе обратных связей регистр, прежде чем вернуться к начальной точке, проходит по циклу из 2ⁿ - 1 чисел, где n - число ячеек. Совершая такой максимальный цикл, регистр проходит по всем возможным числам, за исключением числа из всех нулей, которое является для этого устройства "ловушкой". При обратных связях, показанных на рис. 1, отправляясь от состояния, характеризуемого одними единицами, цикл принимает такой вид, как показано ниже.

Все описанные методы порождают числа, равномерно распределенные в некотором фиксированном интервале; они представляют собой выборки, соответствующие прямоугольному, или равномерному, распределению. Часто требуется получить выборку из распределения какого-то другого типа, например гауссова, или нормального (колоколообразная "кривая ошибок"), либо из отрицательного экспоненциального распределения. Числа, являющиеся выборками из таких распределений, с помощью ряда приемов могут быть выведены из выборок для прямоугольного распределения. Так, если х - выборка для равномерного распределения в интервале 0-1, то - log x есть выборка для отрицательного экспоненциального распределения. Если выборки для равномерного распределения формируются в пачки, причем число выборок в каждой пачке достаточно велико, скажем равно 12, то числа, создаваемые при суммировании каждой пачки, оказываются выборками из распределения, которое приближенно можно считать гауссовым.