3. Доказательство теорем

Привлекательную область применений принципов искусственного интеллекта представляет собой доказательство математических теорем, ибо такого рода деятельность обычно рассматривается как "интеллектуальная", когда ее осуществляют люди. К тому же доказательство теорем считается, в определенном смысле, естественным направлением, в котором следует вести работы по расширению возможностей вычислительных машин.

Первые применения вычислительных машин были преимущественно связаны с выполнением арифметических процедур. Так, в Великобритании работа Бебиджа была главным образом направлена на составление таблиц, необходимых Адмиралтейству, при этом оно осуществлялось принципиально новым методом, более экономичным и безошибочным. Вряд ли стоит напоминать здесь о том, что вычислительные машины способны делать и многое другое, но тем не менее арифметические задачи составляют значительную часть работы существующих вычислительных машин и служат основным экономическим оправданием их существования.

При необходимости вычислительные машины можно запрограммировать для работы с символами и использовать их для решения задач не только арифметики, но и алгебры и формальной логики. Весьма специальные методы программирования, применяемые для таких целей, обычно называют обработкой списков (гл. 13).

Поскольку сфера применения вычислительных машин переместилась от арифметики к оперированию выражениями, содержащими символьные переменные, создание программ доказательства теорем выглядит вполне естественным следующим шагом. Доказательство теорем, по-видимому, можно считать также подходящей областью для изучения методов решения, используемых людьми. Работа Ньюэлла, Саймона и Шоу, приведшая к созданию универсального решателя задач, была с самого начала направлена на моделирование действий, которые совершают люди при решении задач.

Кроме того, существовало мнение, что использование вычислительных машин может произвести переворот в математике, так как позволит обнаружить совершенно новые теоремы. Эта надежда в сколько-нибудь заметной степени не оправдалась, хотя составленные программы и были в состоянии доказывать теоремы и исследовать следствия, вытекающие из известных теорем в ряде областей математики. В течение многих лет разрабатывались методы, предназначенные для доказательства теорем на вычислительных машинах, но еще ни разу не удалось сделать что-нибудь значительное "впервые".

В одной из первых работ, связанных с доказательством теорем, было сделано открытие, которое, как предполагалось, является новым и элегантным доказательством равенства углов при основании равнобедренного треугольника. Обычное доказательство (рис. 2) строится так. Проводится отрезок прямой AD, соединяющий вершину А треугольника с серединой стороны ВС, или же строится перпендикуляр AD к стороне ВС (АВ и АС - равные стороны треугольника ABC). Затем доказывается, что треугольник ABD конгруэнтен треугольнику ACD, откуда следует, что углы ABD и ACD равны между собой.

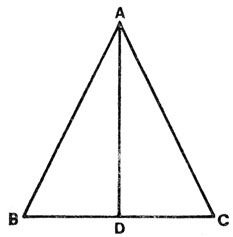
Рис. 2. Равнобедренный треугольник с вспомогательной линией

В доказательстве, найденном с помощью ЭВМ, не требуется построения дополнительного отрезка AD. Оно опирается на доказательство конгруэнтности двух треугольников ABC и АСВ, которые представляют собой один и тот же треугольник при различном порядке указания его сторон. Эти треугольники конгруэнтны, поскольку сторона АВ первого равна стороне АС второго (так как треугольник ABC равнобедренный) и аналогично сторона АС первого треугольника равна стороне АВ второго. Кроме того, разумеется, сторона ВС первого треугольника равна стороне СВ второго. Равенство углов при основании следует из конгруэнтности этих двух треугольников, являющихся зеркальным отображением друг друга.

Это альтернативное доказательство хорошо известного результата отличается особой элегантностью, так как в этом случае отпадает необходимость в построении дополнительного отрезка AD. Строго говоря, это доказательство было обнаружено не на каком-то этапе работы программы вычислительной машины, а лишь в ходе анализа вручную того, что должна была бы делать составленная программа. Тем не менее оно показывает, что автоматизированная математика и в самом деле способна порождать новые доказательства.

В ходе обсуждения этого единичного примера нововведения при машинном доказательстве теорем было высказано много интересных соображений. Дрейфус отметил, что это внешне новое альтернативное доказательство на самом деле не является новым: оно было обнаружено много лет назад, но в значительной степени забыто. Но и независимо от этого замечания чрезмерное выделение конкретного достижения не должно отвлекать наше внимание от того факта, что автоматическое доказательство теорем находит применение в несравненно более развитых разделах математики. Эти применения оказались успешными в том отношении, что программы смогли доказать теоремы, которые по уровню сложности не уступают тем, что доказываются математиками; однако все действительно новые открытия в этой области по-прежнему остаются за людьми.

В своей работе Ньюэлл, Шоу и Саймон заметили, что многие ситуации решения задач можно описать, используя понятия объектов и операторов. В контексте доказательства теорем объектами могут служить алгебраические выражения или выражения формальной логики, тригонометрии или чего-то иного из того раздела математики, с которым работает программа. (Термин универсальный решатель задач использован потому, что программа была составлена так, чтобы быть применимой в различных областях. Имелись ядро программы GPS и различные части "интерфейса" программы, которые согласовывали это ядро с конкретной областью применения.)

Доказательство теоремы можно рассматривать как преобразование одного объекта таким образом, чтобы он совпал с другим. Имеется некое множество операторов, представляющих собой аксиомы и ранее доказанные результаты, на которых должно основываться искомое доказательство. Не все операторы применимы к данному объекту, а лишь несколько из них. Когда оператор применяется к объекту, получается новый объект. Доказательством эквивалентности двух объектов будет служить последовательность применений операторов, с помощью которой один из заданных объектов преобразуется в другой.

Ту же общую идею можно применить к решению задач, с которыми мы сталкиваемся в повседневной действительности. При этом объектами являются "состояния мира", по крайней мере той части его, которая имеет отношение к данной задаче, а операторами - действия, которые может предпринять решающий задачу для того, чтобы изменить одно состояние на другое. Предлагая программу GPS, ее создатели сначала рассматривали применимость соответствующих идей к обыденным ситуациям. Как будет видно из дальнейшего, метод GPS не стал здесь самым мощным методом, как, впрочем, и для доказательства теорем с помощью вычислительной машины, но он часто обсуждается в связи с роботикой. Системы, которыми занимаются в этой области, предназначены для решения реальных задач, обычно связанных с изменением положения совокупности реальных физических предметов, исходя из определенной их конфигурации и с учетом определенных ограничений на допускаемые виды перемещений.

Основной эвристикой, используемой в этих работах, является анализ цели - средства.

Анализ цели - средства

Столь претенциозное название получила одна довольно простая идея, которая имеет, однако, достаточно глубокий смысл. Суть ее состоит в том, что действие, которое следует предпринять, выбирается на основе сопоставления существующего на данный момент положения вещей и того, что необходимо получить в результате решения задачи. Ход решения можно представить в виде замкнутого цикла этапов:

I. Исследуй имеющуюся ситуацию или - для случая доказательства теорем - состояние решения, достигнутое на данный момент времени.

II. Сравни это с тем, что хотелось бы получить, и если отличия нет, то работу можно закончить.

III. Запроси, какой оператор (или операторы) мог бы уменьшить существующее различие.

IV. Последовательно применяй операторы, обнаруженные на этапе III, пока не будет найден оператор, который работает.

V. Возвратись к этапу I.

Чтобы воспользоваться этапом III, необходимо располагать эвристическими правилами, которые связывают имеющиеся в наличии операторы с типами различий, выделяемых на этапе II. Приведенное выше описание этапа IV представляет собой далекое от реальности упрощенное описание процедуры, которую необходимо выполнить. Сказать, что тот или иной оператор "работает", - это равносильно утверждению, что он допускает некую последовательность дальнейших операций, которая заканчивается успехом на этапе II. Таким образом, успех (или неудача) оператора не является очевидным до тех пор, пока не будет проделано еще много итераций из указанных пяти этапов. Необходимо, чтобы в процессе решения задач был предусмотрен способ возвращения назад. Если становится ясно, что используемая последовательность операций не ведет к цели, то необходимо вернуться назад к точке, в которой на этапе IV возможно применение нескольких операторов, но не все из них еще испытаны. Процесс возобновляется с этой точки с использованием еще не опробованного оператора.

Однако, чтобы поступать таким образом, необходимо располагать критерием, который придавал бы точный смысл фразе "Становится ясно, что ... не ведет к цели". При практическом решении задач возникает другая, пожалуй, более серьезная сложность, состоящая в том, что попытка применить некий оператор на этапе IV обычно приводит к возникновению новых задач, которые предстоит решить, а они в свою очередь порождают новые задачи и т. д. Следовательно, процесс решения задач должен быть рекурсивным. Иначе говоря, он должен быть в состоянии рассматривать "задачи внутри задач" путем повторного самозапуска (для "внутренней" задачи) в ходе своей работы (над "внешней" задачей).

В качестве иллюстрации использования анализа цели - средства в обычной жизни Ньюэлл, Шоу и Саймон приводят следующий монолог:

Я хочу доставить своего сына в детский сад. Что составляет различие между имеющейся ситуацией и тем, что мне нужно? Это расстояние. Что может изменить расстояние? Мой автомобиль. Но он неисправен. Что необходимо, чтобы его наладить? Новый аккумулятор. Где найти новый аккумулятор? В автомастерской. Я хочу, чтобы в автомастерской мне поставили новый аккумулятор, но в мастерской не знают, что он мне нужен. В чем трудность? В связи. Что обеспечивает связь? Телефон... и т. д.

Эта последовательность мыслей, возникающая в ходе решения бытовой задачи, является рекурсивной по своему характеру. Проблема доставки ребенка в детский сад поднимает проблему приведения в порядок автомобиля, что в свою очередь порождает проблему контакта с ремонтной мастерской. Здесь достаточно часто возникает необходимость в возвращении процесса назад. Например, ответом на вопрос "Где имеются новые аккумуляторы?" может быть "В автомагазине Смита или в автомагазине Брауна"; тогда может быть принято произвольное решение начать с магазина Смита. Если же обнаружится, что, скажем, телефон магазина Смита неисправен, то придется вернуться к точке, в которой был произведен выбор, - и будет предпринята попытка позвонить в магазин Брауна.

Может случиться, что попытка получить аккумулятор в магазине Брауна также окончится неудачей, тогда возможно возвращение к вопросу "Что может изменить расстояние?", на который возможен более полный набор ответов: "Мой автомобиль, такси, автомобиль соседа, вертолет".

Легко представить себе усложнения, которые могут привести к тому, что метод решения не будет точно таким, как показано выше, или в результате которых принятое решение окажется весьма неэффективным. Возможное усложнение, которое в прежних работах старались игнорировать (и которое не учитывается в доказательстве теорем), - это неопределенность входной информации. Так, в приведенном нами примере весьма маловероятно, чтобы человек, ход мыслей которого мы проследили, был абсолютно уверен, что севший аккумулятор - единственная причина его затруднений с автомобилем. Тогда у него могут возникнуть такие соображения: если он купит аккумулятор, а это не поможет, то у него уже не останется денег на такси, так что, наверное, надежнее сразу начать с такси. В процессе выбора между имеющимися в наличии операторами могут быть использованы дополнительные связи (например, финансового характера).

Кроме усложнений, связанных с неопределенностью входной информации, имеются и другие возможные связи между операторами. Некоторые из них относятся к причинам, ответственным за нерезультативность того или иного оператора. Процесс решения задачи становится более эффективным, если принять во внимание тот факт, что некоторые причины нерезультативности оператора могут быть одинаковыми для нескольких операторов. Если один из операторов оказался неудачным по какой-то определенной причине, то возникает возможность сразу же узнать, стоит ли пробовать другие операторы, определенным образом связанные с этим оператором.

Так, если в нашем примере не удается попасть в детский сад из-за того, что ни в одной автомастерской не нашлось аккумулятора, то имеет смысл вернуться к вопросу "Что может изменить расстояние?" и продолжить поиск решения посредством операторов "такси, автомобиль соседа, вертолет". С другой стороны, если причиной неудачи при попытке воспользоваться собственной автомашиной является то, что единственная дорога, ведущая в детский сад, перекрыта, например, из-за оползня, то подобная причина в равной мере распространяется и на такси, и на автомобиль соседа; тогда единственная оставшаяся возможность состоит в том, чтобы арендовать вертолет. (Едва ли следует говорить, что большинство родителей сделают при этом возврат к цели более высокого порядка, не названной в приведенном монологе, но связанной с обеспечением хорошего воспитания ребенка. При этом родители рассмотрели бы другие возможности достижения этой цели, которые позволили бы обойтись в этот конкретный день без посещения детского сада.)

Усложнения такого рода принимались во внимание при развитии и совершенствовании идеи GPS. Другим примером, который может быть использован для построения подобных умозаключений, может служить двурукий неподвижный робот, предназначенный для взятия предметов. У него имеются два оператора: "взять правой рукой" и "взять левой рукой". Предположим, что вначале была использована правая рука - и робот потерпел неудачу. Если причина неудачи заключается в том, что до предмета невозможно дотянуться, поскольку он слишком далеко расположен или поскольку между ним и правой рукой робота имеется какое-то препятствие, то целесообразно сделать возвращение и попытаться воспользоваться левой рукой. Левая рука робота прикреплена в другом месте, поэтому ей доступна другая область пространства. Если же, однако, причиной неудачи было бы то, что предмет оказался слишком горячим, чтобы его можно было схватить, то неудача с использованием правой руки означает, что неудача ждет робота и при попытке воспользоваться левой рукой. (Предполагается, что для обеих рук допустима одна и та же температура и что они оборудованы сенсорными устройствами, которые не позволяют роботу брать слишком горячие предметы.) Если в системе эта связь между операторами каким-то образом отражена, то после неудачи с правой рукой по указанной причине робот не будет прибегать к напрасной попытке использования левой руки.

Универсальный решатель задач

Программа GPS применяет эвристику анализа цели - средства к доказательству теорем. Математическая ситуация имеет определенные характеристики, и цепочка операций отличается от той, что была описана, следующим образом.

а. Когда на этапе II имеющийся объект сравнивается с требуемым объектом, между ними часто обнаруживается не одно различие. В GPS типы различий располагаются в порядке, призванном отразить среднюю трудность снятия этого различия. Если обнаруживается несколько типов различий, то внимание уделяется тому из них, которое расположено выше по рангу (т. е. относительно которого полагают, что его труднее всего снять). Возможно, что снятие этого различия приведет к новым различиям, более низким по рангу. Там, где сравниваемые объекты имеют "вложенную" структуру (подобно выражениям в алгебре или в формальной логике, которые могут содержать подвыражения, а те в свою очередь также могут содержать подвыражения и т. д.), различия во внешнем выражении получают приоритет над различиями, скрытыми во внутренних выражениях. Ясно, что введение приоритета желательно, поскольку подвыражения могут менять свое место в пределах выражения, когда к нему применяются операторы, в результате чего подвыражения образуют различного рода пары с подвыражениями, содержащимися в целевом объекте.

б. Поскольку число типов различий и число операторов относительно мало, то действия, требуемые на этапе III, можно весьма просто реализовать, используя эвристическую таблицу. Согласно опубликованному описанию системы GPS, она представляет собой двумерную таблицу, строки которой соответствуют типам различий, а столбцы - различным операторам. Крестик, стоящий в месте пересечения той или иной строки с каким-то столбцом, говорит о том, что соответствующий оператор может быть эффективно использован при снятии различия соответствующего типа.

в. Выполнение инструкции "примени оператор" на этапе IV может оказаться непростым делом. Каждый оператор может преобразовывать выражения данного конкретного вида, представленные в списке операторов, посредством некоторого выражения, включающего переменные А, В и С. Прежде чем оператор может быть применен, объект, предназначенный для преобразования, необходимо привести к виду, отвечающему установленной входной форме. Установление такого соответствия связано с приписыванием подходящего "смысла" переменным А, В и С, но может потребовать преобразования всего объекта путем рекурсивного применения метода GPS в целом. Это еще одно направление, где программа GPS действует рекурсивным образом.

Следует отметить, что метод GPS не только является воплощением эвристического метода анализа цели - средства, но и обладает многими другими эвристическими особенностями. Выбор множества типов различий между объектами, ранжирование (упорядочение) их по степени трудности снятия различий, предположение, что в первую очередь требуется обращаться к более "трудным" различиям, - все это эвристики. Все они правдоподобны, и их полезность подтверждается на практике; однако им нельзя дать четких обоснований, которые можно было бы использовать на различных этапах работы алгоритма.

Ранжирование различий в соответствии с оценкой трудности их снятия служит в GPS и другой цели. Эта программа действует, устанавливая определенную последовательность целей, несколько из которых имеют вид "исключить различие такого-то типа между такими-то объектами". С целями подобного типа связывается определенное ранжирование по трудности, и работа GPS направляется таким образом, что какая-то цель отбрасывается, если она не легче другой цели, которой она подчинена. Этот принцип планирования намечен Минским при обсуждении "административных характеристик" эвристических программ (гл. 2). Последовательность шагов программы определяется имеющимися оценками трудности.

Применение GPS к символической логике

Принципы GPS обычно поясняются на примере символической логики, где перед программой может быть поставлена задача доказать что-то, подобное следующему утверждению:

В этом выражении знак "минус" обозначает отрицание не, точка - и, а V-образный значок означает или. Подкова ⊃ означает имплицирует, кроме того, "Р имплицирует Q" эквивалентно "Q или не Р".

Число типов различий, которые можно найти между выражениями, равно шести. (Некоторые из приведенных типов допускают подразбиения. Например, AV включает варианты +ΔV и -ΔV в зависимости от того, находится дополнительная переменная в выражении, которым предстоит манипулировать, или же в целевом выражении. Такие подразбиения не нужны в приведенном примере.) Типы различий перечислены нами в порядке убывания предполагаемой трудности:

ΔV - в одном выражении появляется переменная, которой нет в другом.

ΔN - некоторая переменная встречается в двух выражениях различное число раз.

ΔТ - имеется различие в "знаке" выражений, одно из выражений начинается с символа не, относящегося ко всему выражению.

ΔС - имеется отличие в двоичной связке, т. е. в логическом операторе (и, или или имплицирует), связывающем две переменные или два подвыражения.

ΔG - имеется различие в способах объединения в группы, например P ∨ (Q ∨ R) и (P ∨ Q) ∨ R.

ΔР - имеется различие в положении компонент в двух выражениях, например P ∨ (Q ∨ R) и (Q ∨ R) ∨P.

Существует двенадцать типов операторов, которые используются для изменения выражений. Для некоторых типов операторов с высокими порядковыми номерами требуются два входных объекта, и когда они используются, осуществляется перебор имеющихся объектов (выражений, появившихся в доказательстве ранее) в поисках второго входа для оператора. Для выбранного нами примера потребуется лишь шесть первых операторов, или правил:

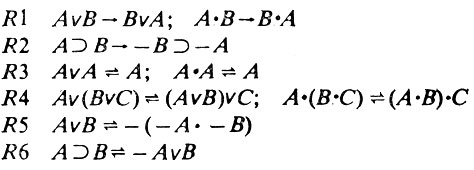
Часть эвристической таблицы, связывающей это множество правил с множеством различий, имеет следующий вид:

Работа программы начинается с установления определенной последовательности целей; причем некоторые из них являются подцелями для других целей, так что в любой момент времени существует "вложенная" структура из целей. Для выбранного нами примера доказательство включает следующие этапы:

Дано: L1 = R · (- P ⊃ Q)

Требуется: L0 = (Q ∨ P) · R

Цель 1: Преобразовать L1 в L0.

Установление соответствия порождает различие в положении (ΔР).

Цель 2: Снять различие ΔР между L1 и L0. Первый найденный оператор R1.

Цель 3: Применить оператор Rl к L1.

Цель 4: Преобразовать L1 в одну из входных форм, приемлемых для R1, обозначаемую как C(R1).

Соответствие устанавливается при A = R и B = - P ⊃ Q.

Создать новый объект: L2 = (- Р ⊃ Q) · R.

Цель 5: Преобразовать L2 в L0.

Приведение в соответствие порождает различие в логических связках (ΔС) в левом подвыражении.

Цель 6: Снять различие ΔС между левой частью L2 и левой частью L0.

Первый найденный оператор R5.

Цель 7: Применить R5 к левой части L2.

Цель 8: Преобразовать левую часть L2 в С (R5).

Приведение в соответствие порождает различие в логических связках (ΔС) в левом подвыражении.

Цель 9: Снять различие ΔС между левой частью L2 и С (R5).

Цель отвергается: различие оказалось не легче, чем различие в случае цели 6.

Второй найденный оператор для цели 6 - R6.

Цель 10: Применить оператор R6 к левой части L2.

Цель 11: Преобразовать левую часть L2 в C(R6).

Соответствие устанавливается при А = - Р и В = Q.

Создать новый объект: L3 = (P ∨ Q) · R.

Цель 12: Преобразовать L3 в L0.

Приведение в соответствие порождает различие в положении переменных (ΔР) в левом подвыражении.

Цель 13: Снять различие ΔР между левыми частями L3 и L0.

Первый найденный оператор R1.

Цель 14: Применить R1 к левой части L3.

Цель 15: Преобразовать левую часть L3 в С (R1).

Соответствие устанавливается при A = P и B = Q.

Создать новый объект: L4 ≠ (Q ∨ Р) · R.

Цель 16: Преобразовать L4 в L0.

Процесс приведения в соответствие показывает, что L4 идентично L0, так что искомая теорема доказана.

В заключение основные этапы доказательства могут быть сведены вместе в достаточно компактную, форму. Следует подчеркнуть, что мы привели весьма простой пример доказательства и что программа GPS может давать гораздо более впечатляющие результаты.