4. Доказательство теорем другим методом

Универсальный решатель задач наиболее интересен как модель для решения задач такого типа, которые обычно возникают перед человеком. Различные варианты этого решателя встречаются среди систем планирования для роботов, где проблемные ситуации ближе к привычным человеку, чем ситуации, характерные для процесса доказательства теорем. Вместе с тем установлено, что когда возникает необходимость именно в доказательстве математических теорем, более эффективным и более подходящим для различных областей математики является другой подход. По мнению автора, подход с позиции GPS более предпочтителен в силу его "естественности", однако многие другие исследователи придерживаются иной точки зрения, используя альтернативный подход, получивший название метода резолюции.

Метод резолюции

Суть этого метода состоит в том, чтобы исходя из некоторого множества утверждений, называемых предложениями, вывести из этого множества другие предложения. Исходные предложения формулируются тем, кто использует данный метод, таким образом, чтобы они отражали аксиомы математической системы, в рамках которой производится работа, и предположения, на основе которых требуется доказать теорему. В исходные предложения включают также отрицание того утверждения, которое следует доказать. Смысл включения такого отрицания, а не самого утверждения заключается в том, что возникновение в процессе доказательства противоречия означает, что результат доказан.

Обычно предложение представляет собой цепочку элементарных выражений, называемых литералами, где каждый литерал является функцией одного или нескольких аргументов. Предполагается, что литералы в предложении отделены друг от друга логическим оператором ИЛИ, однако при записи его часто опускают.

Поясним сказанное на простом примере, заимствованном из книги Слейгла [1]. Автор показывает, как используется метод резолюции для доказательства следующего утверждения:

Если палец представляет собой часть кисти, а кисть - часть руки, а рука - часть человека, то требуется доказать, что палец является частью человека.

Одна из причин, по которой метод резолюции получил столь широкое распространение, состоит в том, что данный метод допускает использование такого числа различных типов атомарных формул, которое необходимо для представления интересующей нас задачи. Атомарная формула имеет вид логической функции и представляет собой утверждение, которое является либо истинным, либо ложным. Для доказательства приведенной выше теоремы нам потребуется лишь один тип атомарной формулы, в которой используется символ Р, выражающий отношение "быть частью". Утверждение Р(х, у) истинно, если х есть часть у, и ложно в противном случае. Если мы обозначим буквами п, к, р, ч соответственно палец, кисть, руку и человека, то верно следующее:

Р(п, к)    Р(к, р)    Р(р, ч)

Нам требуется доказать Р (п, ч), и мы должны включить в число начальных предложений отрицание, или обратное утверждение, которое записывается в виде - Р(п, ч), где знак "минус" соответствует отрицанию не. Литерал указывает либо на атомарную формулу, либо на отрицание атомарной формулы.

Рассматриваемую теорему невозможно доказать без введения аксиомы транзитивности, определяющей отношение Р - "быть частью". Эту аксиому можно записать так:

Для целей автоматического доказательства теорем более целесообразно представить аксиому транзитивности в виде, множества литералов, объединенных в предложение посредством (подразумеваемого) оператора или. Таким образом, вместо того чтобы формулировать аксиому (как мы это делали выше) посредством утверждения, что если две вещи истинны, то должна быть истинной и третья, можно сказать, что либо третья истинна, либо одна из первых двух^* ложна. Формально имеем

Р(х, z)  или  - Р(х, у)  или  -Р(у, z),

а поскольку частое употребление оператора или весьма утомительно, его обычно опускают, тогда приведенная выше запись будет выглядеть как

Р(х, z)   - Р(х, у)   - Р (у, z).

^* (Либо обе посылки одновременно ложны. - Прим. ред.)

Теперь мы можем записать множество предложений, которое должно быть отправной точкой для доказательства, следующим образом:

1. Р(х, z)   - Р(х, у)   - Р(у, z) 
2. Р(п, к) 
3. Р(к, р) 
4. Р(р, ч) 
5. - Р(п, ч).

Символы п, к, р, ч - константы, имеющие от предложения к предложению одно и то же значение. С другой стороны, символы х, у и z появляются в предложении, которое истинно, какие бы новые величины в него ни подставлялись. Вместо х, у и z подстановки допускаются, если они делаются целиком во всем предложении.

Основной операцией, определяющей данный метод, является резолюция между двумя литералами. Необходимо найти в различных предложениях два литерала, такие, что после допустимых подстановок один из них становится отрицанием другого. Например, в рассматриваемом доказательстве можно получить резолюцию литерала из предложения 2 со вторым литералом из предложения 1. Эти два литерала соответственно Р(п, к) и - Р(х, у). Можно добиться, чтобы один из этих литералов был отрицанием другого, подставив п вместо х и к вместо у во всем предложении 1. Предложение 1 тогда принимает вид

Р(к, z)   - Р (п, h)   - Р (к, z),

а предложение 2 сохраняется:

Так как предложение 2 утверждает, что Р(п, к) истинно, то второй литерал в модифицированном предложении 1 может быть исключен; тогда получаем новое предложение:

6. Р(п, z)   - Р(к, z).

То, что это новое предложение было выведено путем резолюции второго литерала в предложении 1 с единственным литералом предложения 2, может быть указано в конце строки следующим образом:

6. Р(п, z)   - Р(к, z)   р(1б, 2)*.

^* (Индексы а, б, в, стоящие рядом с цифрами, указывают, что использовался соответственно первый, второй или третий литерал данного предложения. - Прим. перев.)

Дальнейшие резолюции в конечном итоге приводят к предложению, вообще не содержащему литералов, что указывает на противоречие и, следовательно, на успешное доказательство теоремы. Возможное продолжение доказательства могло бы выглядеть, например, так:

 7.  Р(п, р)                    р(3, 6б) 
 8. -Р(р, ч)                    р(5, 6а)
 9.  Р(х, р)   - Р(х, п)        р(1в, 2) 
10.  P(h, z)   - P(p, z)        р(3, 1б) 
11.  Р(Р, ч)                    р(4, 10б) 
12.  Противоречие               р(8, 11).

Предложения с номерами 7 и 9 на самом деле не потребовались, и их можно было бы без труда исключить при "причесывании" доказательства. Мы их включили здесь по той причине, что они бы потребовались, если бы последовательность резолюций определялась некой конкретной эвристикой, которую мы опишем позже.

Во всех резолюциях, необходимых в нашем простом доказательстве, один из литералов был в 1-предложении (предложение лишь с одним литералом; предложение с двумя литералами обозначается как 2-предложение и т. д.). Резолюция возможна также между двумя литералами, ни один из которых не встречается в 1-предложении. Предположим, например, что каждый из литералов появляется в 3-предложении и что эти 3-предложения после подставок, приводящих к появлению литералов, которые оказываются отрицанием друг друга, имеют вид

А     В      С

D     Е    - С,

где А, В, D и Е - литералы, С - атомарная формула.

Первое из этих предложений показывает, что если С ложно, то либо А, либо В должно быть истинным^*. Второе предложение показывает, что если С истинно, то либо D, либо Е должно быть истинным. Следовательно, можно исключить С и утверждать, что хотя бы один из оставшихся четырех литералов должен быть истинным. После резолюции возникает следующее предложение:

^* (См. примечание на с. 67.)

А    В    D    Е.

При резолюции литерала в m-предложении с литералом в n-предложении образуется новое предложение, не более длинное чем (m + n - 2)-предложение. В приведенном выше примере два 3-предложения привели к 4-предложению, но если не все литералы А, В, D и Е различны, то в результате мы получим более короткое предложение, поскольку повторение литералов было бы бессмысленным.

Возможно, что возникнет предложение, содержащее некоторый литерал и его отрицание. Такое предложение, очевидно, является истинным, так как представляет собой просто тавтологию. Его следует исключить из доказательства, так как оно будет бесполезным для последующих выводов.

Существует еще один способ создания новых предложений, отличный от резолюции, - это метод факторизации. Если имеется такая подстановка, которую можно осуществить в n-предложении (n > 1) и которая делает два или более его литералов идентичными, то все, кроме одного, образованные таким образом литералы можно исключить. При этом возникает предложение, содержащее менее n литералов. В дальнейшем мы приведем пример доказательства с использованием факторизации.

Более выразительный пример

Доказательство утверждения типа "палец является частью кисти и т. д." помогает пояснить общую идею метода резолюции, но, безусловно, это слишком простой пример использования такого метода. Чтобы убедить читателя в эффективности и ценности применения метода резолюции, рассмотрим доказательство следующей теоремы абстрактной алгебры:

Если ассоциативная система содержит какой-то единичный элемент и квадрат каждого элемента представляет собой единичный элемент, то такая система коммутативна.

Данная система включает операцию, которую можно назвать "умножением", эту операцию обозначают точкой. Если е - единичный элемент, то отсюда следует, что

для всех х.

Свойство ассоциативности означает, ч

для всех х, у и z.

Чтобы выразить эти утверждения в требуемой форме, вводится специальный вид атомарной формулы Р(х, у, z), которая становится истинной, если x·y = z, и ложной в противном случае. Тогда существование единичного элемента утверждается с помощью следующих предложений:

Представить свойство ассоциативности в требуемой форме оказывается несколько более трудным делом. Поскольку число переменных в доказательстве может стать достаточно большим (в частности, и по той причине, что часто приходится переименовывать переменные), вместо последовательности букв х, у, z удобно пользоваться переменными с индексами, скажем, х₁, х₂, х₃, ... .

Тогда свойство ассоциативности может быть выражено следующим образом:

(То, что здесь мы использовали x₄ вместо обычно принятого х₃, не имеет особого значения, однако это приводит к несколько более изящному окончательному результату, чем в случае, когда индексы идут подряд.)

На самом деле в таком представлении свойства ассоциативности содержатся два утверждения. Истинность левой части гарантирует истинность правой, и наоборот.

Если х₁ · х₂ = х₃ и x₂ · x₄ = x₅, то левая часть уравнения (1) равна х₃ · x₄, а правая его часть - х₁ · x₅.

Если же х₁ · x₂ = x₃ и x₂ · x₄ = x₅ (как выше) и x₁ · x₅ = x₆, то соотношение (1) таким образом утверждает, что x₃ · x₄ = x₆.

Используя рассмотренный ранее метод, мы можем записать это утверждение в виде предложения

- Р(х1, х2, х3)   - Р(x2, х4, х5)   - Р(х1, х5, х6)   Р(х3, х4, x6).

Соотношение (1) содержит также утверждение (прямое и обратное) о том, что если х₁ · x₂ = x₃, x₂ · x₄ = x₅ (как выше) и x₃ · x₄ = x₆, x₁ · x₅ = x₆. Это утверждение, будучи записано в соответствующей форме, принимает вид

- Р(х1, х2, х3)   - Р(x2, х4, х5)   - Р(х3, х, х6)   Р(х1, х5, x6).

Другое утверждение доказываемой теоремы, а именно что квадрат каждого элемента представляет собой единичный элемент, можно записать и виде такого предложения:

Следует доказать, что система коммутативна, т. е. что х·у равно у·х для всех х и у. Отрицание этого утверждения формулируется так: имеются величины а и b, такие, что а·b ≠ b·а. Утверждение а·b = с можно выразить в виде двух предложений

Начальные предложения для доказательства можно теперь собрать вместе:

1. Р(е, х1, х1) 
2. Р(х1, е, х1) 
3. - Р(х1, х2, х3)   - Р(х2, x4, х5)   - P(x1, х5, х6)   Р(х3, х4, х6) 
4. - Р(х1, х2, х3)   - Р(х2, х4, x5)   - Р(х3, х4, х6)   Р(х1, х5, х6) 
5. P(x1, x1, e) 
6. Р(а, b, с) 
7. - Р(b, а, с).

Следует заметить, что, хотя константы а, b, с, и е имеют один и тот же смысл во всех предложениях, переменные x₁, х₂, ... являются локальными для того предложения, в котором они возникают. Переменная x₁, используемая в предложении 1, никак не связана с одноименными переменными, входящими в предложения 2-5. Поэтому когда в ходе резолюции предложения объединяются, некоторые из переменных необходимо переименовать, так чтобы они отличались от идентично обозначенных переменных в другом предложении.

Теперь произведем доказательство теоремы на основе последовательности резолюций; однако на этой стадии мы не будем вдаваться в объяснения по поводу того, почему на каждом этапе доказательства из бесчисленного числа возможностей выбирается та или иная конкретная резолюция.

Первый этап состоит в нахождении резолюции второго литерала предложения 3 с единственным литералом предложения 5. Переменные, использованные в предложении 5, позволяют обойтись без их переименования; таким образом, среди подстановок, делаемых в предложении 3, должны быть такие:

х2 → х1    х4 → х1    х5 → е.

Поскольку "старое" x₁ в предложении 3 оставлять нельзя, необходимо сделать подстановку:

а обозначения х₃, x₅ и х₆ можно оставить без изменения. Новое предложение, которое получается в результате резолюции, имеет вид

8. - Р(х2, x1, х3)   - Р(х2, е, x6)   Р(х3, х1, х6).

На следующем этапе производится резолюция первого литерала предложения 4 с предложением 5. При этом переменные предложения 5 снова сохраняют свои наименования, так же как х₁ из предложения 4. Другие переменные предложения 4 переименовывают следующим образом:

х2 → x1 х3 → е,

а х₄, х₅ и х₆ сохраняют старые наименования. В ходе резолюции получаем новое предложение:

9. - Р(х1, х4, х5)   - P(e, x4, x6)   - P(x1, x5, x6).

При резолюции первого литерала предложения 3 с единственным литералом предложения 6 необходимо, чтобы переменные предложения 3 были заменены на константы следующим образом:

х1 → а    х2 → b    х3 → с,

при этом переменные с более высокими индексами сохраняют свои наименования. В результате имеем

10. - P(b, х4, x5)   - P(a, x5, x6)   P(c, x4, x6).

Для резолюции единственного литерала предложения 1 со вторым литералом предложения 9 требуется переименовать переменные в предложении 9 следующим образом:

х4 → х1   x6 → х1   х1 → х2,

причем х₅ сохраняется. В результате получаем

11. - Р(х2, х1, х5)   Р(х2, х5, х1).

Для резолюции единственного литерала предложения 2 со вторым литералом предложения 8 необходимо переименовать переменные в предложении 8 следующим образом:

x2 → x1   x6 → x1   x1 → x2,

причем х₃ сохраняет старое наименование. В результате имеем

12. - Р(х1, х2, x3)   P(x3, x2, x1).

На следующем этапе возникает ситуация, с которой мы раньше не встречались, поскольку теперь подстановки делаются в обоих предложениях с тем, чтобы литералы стали отрицанием друг друга. Единственный литерал предложения 5 разрешается с первым литералом предложения 10. Для этого в предложении 5 нужно сделать подстановку

а в предложении 10 следующие подстановки:

х4 → b    х5 → е,

в то время как x₆ сохраняет свое наименование. В результате имеем

13. - Р(а, е, x6)    Р(с, b, x6).

Теперь единственный литерал предложения 2 разрешается с первым литералом предложения 13 при подстановке в предложении 2

и подстановке в предложении 13

что дает

Резолюция этого предложения с первым литералом предложения 1 приводит к

а резолюция этого предложения с первым, литералом предложения 12 дает

Резолюция этого предложения с предложением 7 порождает предложение нулевой длины, что указывает на

и, следовательно, на то, что интересующая нас теорема доказана.

Этот пример взят из доказательства, проведенного на вычислительной машине и описанного в работе Лакхэма, одного из пионеров данного метода. Это доказательство (при рассмотрении его этап за этапом) выглядит довольно сложным, хотя определение начального множества предложений (1-7) оказалось делом довольно простым. Главная же трудность в осуществлении доказательства на машине была связана с представлением свойства ассоциативности.

Дизъюнктивная форма

Преобразование утверждения теоремы в эквивалентное множество дизъюнктивных предложений (т. е. предложений, составляющие литералы которых связаны логическим оператором или) не всегда оказывается простой задачей. Если речь идет об автоматическом методе доказательства теорем, то необходимо уделить внимание и этой стороне вопроса.

Поэтому для преобразования утверждения теоремы, сформулированного на языке исчисления предикатов, в эквивалентное утверждение, выраженное в форме предложений, был разработан алгоритмический метод.

В приведенных нами примерах не затрагивался вопрос, который обычно возникает, когда требующая доказательства теорема содержит утверждения, включающие слова "для всех" или какие-либо другие слова, указывающие на определенную общность утверждения.

В качестве иллюстрации сказанного рассмотрим алгебраическую теорему, также заимствованную из книги Слейгла [1]:

В любой ассоциативной системе, которая имеет левые и правые решения s и t для всех уравнений s·x = y и x·t = y, существует правый единичный элемент.

На первый взгляд может показаться, что существование левого решения s должно было бы следовать из предложения

где Р имеет тот же смысл, что и в последнем из рассмотренных ранее примеров.

Чтобы это предложение имело точный смысл, необходимо знать, рассматривается ли s как константа (подобно п, к, р, ч в примере "палец - часть кисти") или как переменная, допускающая любую подстановку. Легко заметить, что ни одна из этих возможностей не является удовлетворительной. С одной стороны, никакое значение константы, приписанное s, не было бы пригодно для всех величин х и у. А с другой стороны, было бы также неправильно допустить, чтобы s было переменной, подобной х и у, ибо это означало бы, что любая величина, приписанная s, была бы решением.

Эта трудность преодолевается таким образом: указывается, что подходящим значением для s является некая функция переменных х и у. Тогда предложение записывается в виде

где функция g остается неопределенной. Функции, используемые таким образом, называют сколемовскими функциями.

Аналогично для правого решения имеем

Свойство ассоциативности можно выразить в той же форме, как и прежде. (В настоящем примере достаточно включить одно из предложений, выражающих свойство ассоциативности.)

Требуется доказать, что существует правый единичный элемент; это утверждение выражают таким предложением:

Однако нам нужно не это утверждение, а утверждение, обратное ему, т. е. гласящее, что не существует правого единичного элемента. Простое отрицание вида

нас не устраивает, ибо оно означает только, что существует некий элемент, такой, что его использование в качестве правого множителя никогда не даст того же самого результата, как умножение на правый единичный элемент.

Чтобы ввести требуемое отрицание утверждения, необходимо рассмотреть правое умножение на переменную х, в качестве которой может быть подставлена любая величина. Говоря, что х не является правым единичным элементом, мы тем самым утверждаем, что для любого х может быть найдена величина k, такая, что

Поскольку для каждой величины х необходимо найти лишь одно значение k, уместно воспользоваться сколемовской функцией:

или

Теперь доказательство оказывается весьма коротким (предложение 3 есть часть представления свойства ассоциативности):

1.   P(g(x, у), х, у) 
2.   Р(х, h(x, у), у) 
3. - Р(u, v, w)  - Р (v, х, у)  - Р (u, у, z)  Р(w, х, z) 
4. - P(k(x), x, k(x)).

Первый этап состоит в факторизации предложения 3, которая осуществляется путем таких подстановок, в результате которых первый и третий литералы становятся идентичными. Это достигается подстановкой

y → v     z → w.

После нее получаем

- Р(u, v, w)    - P(v, х, v)    - Р(u, v, w)    P(w, x, w).

Отсюда можно исключить лишний литерал, что дает

5. - Р(u, v, w)    - P(v, x, v)    P(w, x, w).

Затем резолюции производятся следующим образом:

6. - Р(х, z, x)    P(y, z, у)     р(1,5а)

(переменную х в предложении 4 заменяем на 2, чтобы отличить ее от х в предложении 1)

7. - Р(х, z, х)       р(4,6б)

8. Противоречие.      (2,7)

Как видим, сколемовские функции в ходе последующих резолюций исчезают (что весьма удобно), но вместе с тем они играют полезную роль, позволяя контролировать, какие резолюции являются возможными.

Эвристики

В тех доказательствах, которые мы здесь рассмотрели, на большинстве этапов можно было произвести несколько резолюций. Шаги, которые в конечном счете оказываются бесполезными, можно отбросить в процессе ретроспективного "наведения порядка", подобно тому как мы отбросили предложения 7 и 9 в примере с доказательством теоремы "палец есть часть кисти". Такое "причесывание" в ходе доказательства создает ощущение, что для выбора следующего шага имеются более разумные основания, чем это было на самом деле. Однако очень важно, чтобы в ходе доказательства не создавалось много "тупиков", ибо в противном случае время поиска доказательства может оказаться неприемлемо большим. При этом можно также столкнуться с комбинаторным взрывом.

Поэтому в действительности нам нужно иметь множество эвристических правил, которые при каждом шаге доказательства указывали бы, какую из возможных резолюций (или факторизации) следует осуществить. Объем вычислений в процессе поиска доказательства существенно зависит от используемых эвристик. При реализации метода резолюции проблема нахождения эффективных эвристик является центральной.

Одна из полезных эвристик - стратегия предпочтения одночленам. Под одночленом понимается 1-предложение. При такой стратегии в каждой последующей резолюции используется 1-предложение, и так продолжается до тех пор, пока возможны резолюции подобного рода. (Разумеется, все последующие резолюции и факторизации должны быть такими, какие ранее не встречались.)

В тех случаях, когда возможно использование более одной резолюции с 1-предложением, предпочтение отдается резолюциям, дающим более короткие новые предложения. Так, резолюция между 1-предложением и 2-предложением (создающая новое 1-предложение) получает приоритет перед резолюцией между 1-предложением и 3-предложением. Аналогично если невозможна резолюция с 1-предложением, то предпочтение отдается резолюциям, порождающим более короткие новые предложения. Таким образом, резолюция 2-предложения с другим 2-предложением (которая обычно порождает другое 2-предложение) имеет преимущество перед резолюцией 2-предложения с 3-предложением. Однако приоритет, даваемый одночленам, означает, что резолюция 1-предложения даже с 5-предложением получает приоритет по сравнению с любым из предыдущих случаев.

Доказательство, которое мы производили в задаче "палец - часть кисти", в точности следует стратегии предпочтения одночленам. Вначале единственной возможной резолюцией является резолюция между 1-предложением и 3-предложением, которое имеет номер 1. (Любые резолюции между отрицательным 1-предложением и любым из других 1-предложений исключены, поскольку они содержат константы.) Первая из выполненных резолюций - это резолюция между первым 1-предложением в последовательности и первым подходящим литералом в предложении 1.

Возможны и другие резолюции с первым предложением, но как только появляется 2-предложение под номером 6, приоритет получают резолюции с этим предложением. Первым из 1-предложений, для которого возможна резолюция с предложением 6, является третье предложение. По достижении девятого шага возможности использования предложения 6 оказываются исчерпанными, так что на следующих двух этапах вновь используется предложение под номером 1.

Стратегия предпочтения одночленам воплощает принцип предпочтения коротким предложениям. Подобная стратегия оправдывается тем, что желаемым выходом является получение противоречия, соответствующего самому короткому предложению, а именно предложению нулевой длины.

Другой полезной эвристикой считается стратегия опорного множества. При ее использовании некоторые из начальных предложений берутся за аксиомы, а остальные предложения составляют опорное множество. При этом соблюдается правило, что между аксиомами резолюции не допускаются. В примере "палец - часть кисти" первые четыре предложения могут быть выделены как аксиомы - и тогда первой резолюцией должна быть резолюция предложения 5 с первым литералом предложения 1, что дает

6'. - Р(f, y)     - Р(y,m).

Комбинация стратегии предпочтения одночленам и стратегии опорного множества приводит для этого примера к доказательству, которое на один шаг короче того доказательства, которое мы получаем при использовании одной лишь стратегии предпочтения одночленам.

Типы атомарных формул

В каждом из рассмотренных нами примеров использовались атомарные формулы лишь одного типа. В первом примере Р(х, у) истинно, если х - часть у. В других примерах Р(х, у, z) истинно, если х · у = z.

Однако совсем необязательно ограничиваться атомарными формулами только одного типа. В приложении к теории чисел, например, полезно в ходе доказательства иметь атомарную формулу Р(х), такую, что она истинна, если х - простое число, а также формулу D(x, y), которая истинна, если х делится на у без остатка.

Приведем простой пример (Слейгл давал его студентам в качестве упражнения) доказательства следующего предложения:

Если каждый человек, обманывающий других, является мошенником и если каждый, кто потворствует мошеннику, также считается мошенником, и существует робкий человек, потворствующий обманщику, то некий мошенник является робким человеком.

Для обозначения соответственно мошенничества, обмана и робости используем атомарные формулы М(x), О(х) и Р(х), а П(х, у) представляет собой еще одну формулу, которая истинна, если х поощряет у.

Тогда тот факт, что каждый обманщик является мошенником, выражается следующим предложением

1. - О(х)    М(х).

То, что каждый, кто потворствует мошеннику, является мошенником, записывается предложением

2. - П(х, у)    -M(у.)    M(х).

Существование робкого человека, потворствующего обманщику, представляется в виде следующих предложений:

3. Р(а)

4. O(b)

5. П(а, b).

Отрицание заключения "некий мошенник является робким человеком" дается предложением

6. - М(x)    - Р(х),

поскольку оно означает, что любой человек либо не является мошенником, либо не является робким человеком.

Стратегия предпочтения одночленам рекомендует рассмотреть резолюцию предложения 3 со вторым литералом в предложении 6, что приводит к

 7. М(x)               р(3, 6б)

а затем

 8.   М(b)            р(1а, 4) 
 9. - Р(b)            р(6а, 8) 
10. - М(b)   М(а)     р(2а, 5) 
11. - М(b)            р(7, 10б) 
12. Противоречие      р(8, 11)

Автоматическая математика

До сих пор при составлении соответствующих программ основное внимание уделялось автоматизации доказательства теорем в предположении, что формулировка доказываемой теоремы осуществляется за счет какого-то внешнего источника. Более привлекательным, однако, было бы ее порождение на основе некоторого множества аксиом и ранее доказанных результатов. Можно сделать, чтобы такая программа работала с использованием той или иной модификации метода резолюции.

Одна из трудностей, возникающих при поиске следствий из уже доказанных теорем, состоит в том, что программа должна оценивать некоторое утверждение как интересную новую теорему или "понимать", что это утверждение имеет достаточную потенциальную значимость, чтобы хранить его в рабочем пространстве. Была проделана определенная работа по поиску эвристик отбора интересных результатов. Обычно такие результаты отличаются тем, что могут быть выражены достаточно кратко, но их нельзя за небольшое число шагов вывести из других интересных результатов.

Интересные работы по автоматической математике были проведены известным советским ученым В. М. Глушковым и его сотрудниками в Институте кибернетики в г. Киеве. Согласно их предположению, вычислительная машина должна быть хранилищем математических теорем, дополненным специальным математическим журналом. Любой результат может быть подвергнут проверке с точки зрения как верности, так и новизны. Это и есть пример сотрудничества человека и машинного интеллекта. Такое сотрудничество, по-видимому, будет играть важную роль в грядущих применениях искусственного интеллекта (гл. 15).

Нестандартные методы доказательства

Не всегда математическая теория развивается столь упорядоченным образом, как это выглядит в обсуждениях, подобных нашему. Иногда доказательство может строиться не только на результатах, полученных ранее в той же области математики.

Так, Пойа показал, что некоторые интересные результаты, касающиеся геометрии на плоскости, можно вывести, вырезая из картона определенные фигуры и каким-то образом комбинируя их между собой. Впечатляющим примером доказательства такого рода может служить следующая теорема, которую Пойа взял из работы одного из своих предшественников:

Площадь многоугольника, вписанного в окружность, больше площади любого другого многоугольника с соответственно равными сторонами. (Стороны одинаковы как по длине, так и по порядку следования.)

Доказательство основывается на следующей изопериметрической теореме: "Из всех плоских фигур равного периметра круг имеет максимальную площадь".

Первый результат можно доказать, предполагая, что сегменты (заштрихованные области на рис. 3), образующиеся между сторонами многоугольника и описанной окружностью, вырезаны из картона, и мы можем переместить их в другое положение. Необходимо также предположить, что стороны многоугольника и, следовательно, основания сегментов соединены между собой шарнирами, так что мы можем деформировать фигуру, как это показано на рис. 4.

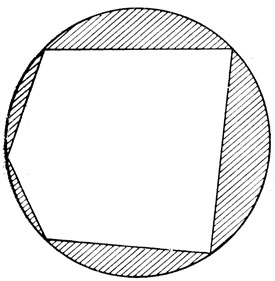
Рис. 3. Многоугольник, вписанный в окружность

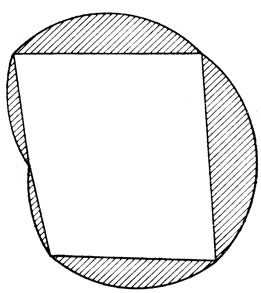
Рис. 4. Деформированный многоугольник. Сегменты круга скользят так, будто они соединены шарнирами

Любая подобная деформация может привести лишь к уменьшению общей площади замкнутой фигуры, так как ее периметр остается равным периметру окружности: это следует из изопериметрической теоремы. Однако общая площадь фигуры, изображенной на рис. 4, включает в себя площадь нового, измененной формы, многоугольника плюс площадь заштрихованных сегментов. Поскольку последние остались неизменными, площадь деформированного многоугольника должна быть меньше площади многоугольника, представленного на рис. 3, причем это справедливо для любого вида искажения, - следовательно, теорема доказана.

В действительности это доказательство не открывает новых возможностей в математике, поскольку в то время, когда оно было осуществлено, теорема изопериметричности не была доказана, хотя и казалась вполне правдоподобной. Пойа доказывает изопериметрическую теорему, опираясь на доказательство приведенного выше результата для многоугольника, но проделанное другим методом, после чего он выводит из полученного результата изопериметрическую теорему.

Хотя в конечном итоге ценность приведенного нами доказательства может оказаться сомнительной, оно, безусловно, показывает, что иногда для доказательства можно воспользоваться нестандартным методом, применив его так, чтобы доказательство выглядело вполне убедительным. Однако методы доказательства, использующие вычислительную технику, скорее всего будут ограничиваться простыми математическими конструкциями, построенными с помощью линейки и циркуля, и аргументами, непосредственно следующими из аксиом евклидовой геометрии. Мы же здесь показали, что при решении различных задач в принципе человек в состоянии воспользоваться несравненно более богатым "ассортиментом" аксиом. Возможно, кто-то возразит, что этот "ассортимент" недопустим, поскольку каждая отрасль математики должна опираться на некоторый изначально установленный набор аксиом. Однако нестандартные методы имеют по крайней мере эвристическую ценность: если теорему с очевидностью удалось "доказать" такими эвристическими методами, то, вероятно, и вполне "законное" доказательство со временем удастся найти.