8. Анализ сцен

Существуют важные случаи восприятия, которые нельзя представить как задачу распознавания образов, принадлежащих некоторому конечному множеству возможностей. Даже если это и можно сделать в принципе, то возникают, как уже отмечалось, трудности, связанные с задачей разделения дискретных объектов. В последние годы особенно в связи с развитием роботики большое внимание уделяется анализу сцен.

И хотя многие важные проблемы здесь остаются еще не решенными, достигнут определенный успех в создании методов интерпретации контурных рисунков многогранных объектов и групп таких объектов. На рис. 20 приведен пример ситуации, которая поддается анализу (см. работу Минского и Пейперта [1]).

Интерпретация контурных рисунков, вероятно, гораздо теснее связана с более общей проблемой анализа сцен, чем это может показаться на первый взгляд. Первый этап анализа зрительных сцен, по-видимому, заключается в выделении границ тел. Именно с этого, как правило, начинается работа вычислительных программ; как показывают исследования Хьюбеля и Визеля (гл. 12), что-то подобное происходит и в зрительных центрах головного мозга животных.

Хьюбель и Визель установили, что границы и отрезки линий выделяются в мозге на одном и том же уровне обработки. Следовательно, весьма вероятно, что подобным образом они учитываются и в ходе дальнейшей обработки информации в мозге животного. Несомненно, что люди с готовностью принимают контурные рисунки за изображение твердых тел; это согласуется с предположением, что изображения твердых тел сначала обрабатываются в мозге так, что становятся чем-то вроде контурных рисунков.

Нет необходимости говорить, что мир не составлен из многогранников и что контурные изображения предметов реального мира не состоят исключительно из прямых линий. Рисунки, образованные отрезками прямых, - это лишь отправная точка, и в настоящее время ведется работа по созданию методики, предназначенной для анализа изображений с криволинейными контурами.

Анализ рисунка, подобного рис. 20, опирается на разметку линий в соответствии с тем, что они представляют на этом изображении. Линия может быть отнесена к одному из следующих типов:

а) вогнутый край;

б) выпуклый край, причем обе примыкающие поверхности видны;

в) выпуклый край, но видна лишь одна из примыкающих поверхностей (к этой группе принадлежат линии, которые образуют внешние контуры объектов).

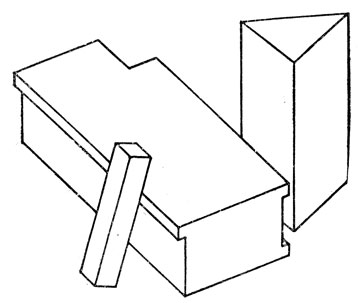
Рис. 20. Контурное изображение группы многогранников

Предполагается, что объекты, изображенные на рисунке, таковы, что в одной тачке может встретиться не более трех плоскостей (так что, например, прямоугольные пирамиды из рассмотрения исключаются). Принимается также, что позиция наблюдателя такова, что при небольшом изменении ее множество видимых им углов и пересечений линий не изменяется.

Самое простое, с чего может начать программа при интерпретации контурного рисунка, подобного рис. 20, - проведение разметки всех линий с тем, чтобы указать, относятся ли они к разновидности (а), (б) или (в). Такая система разметки называется разметкой Хаффмана - Клюса - по имени двух исследователей, которые независимо друг от друга ее разработали.

Обычно линии типа (а) помечают знаком (-), линии типа (б) - знаком (+). Несколько более сложной оказывается разметка линий типа (в), поскольку для них желательно указать, с какой стороны находится видимая поверхность. Обычно их помечают стрелочкой, идущей в направлении видимой поверхности объекта.

Нетрудно понять, что на те комбинации типов линий, которые могут встретиться в каком-то узле, накладываются определенные ограничения. Они оказываются настолько сильными, что на конкретном рисунке (который представляет собой изображение некоего реально возможного объекта, подчиняющегося двум указанным выше предположениям) возможен лишь один способ разметки.

Внешний край изображения может быть образован лишь линиями типа (в), причем направление стрелок должно быть таково, что они следуют друг за другом по часовой стрелке.

Ограничения, обеспечивающие разметку всех линий, основываются на том, что (при указанных выше предположениях) у многогранника возможно лишь четыре типа углов. Они показаны на рис. 21; на рис. 22 отмечены возможные позиции наблюдателя и разметки примыкающих линий. Возможны также лишь три типа Т-соединений (рис. 23).

Рис. 21. Четыре возможных типа углов в многогранниках (по Рафаэлу [2]). Верхние горизонтальные поверхности помечены стоящими на них фигурками; еще одна фигурка спускается по вертикальной поверхности

Рис. 22. Всевозможные способы, с помощью которых четыре типа углов могут быть представлены как Y-сочленения или как изгибы, с разметкой примыкающих линий (по Рафаэлу [2]). Нижние горизонтальные поверхности указываются фигурками, висящими на веревочных лестницах

Рис. 23. Четыре возможных типа T-соединений с разметкой примыкающих линий (по Рафаэлу [2])

На рис. 24 представлен пример изображения, которое можно проанализировать с применением разметки Хаффмана - Клюса. Оно несколько проще, чем изображение на рис. 20. (Однако и рис. 20 вполне поддается анализу с помощью существующих программ.) После того как разметка закончена, появляется возможность перечислить отдельные объекты на рисунке и указать их поверхности. Чтобы это сделать, необходимо рассмотреть множества линий, которые служат точным продолжением друг друга (как те две пары вертикальных линий на рис. 24, которые, очевидно, являются краями треугольной призмы), и связать их в одну линию.

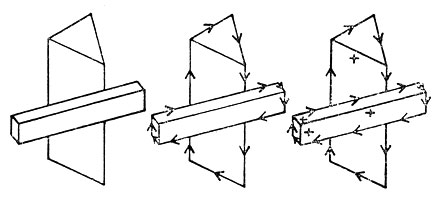
Рис. 24. Контурные рисунки без разметки, с разметкой граничных линий и с полной разметкой

Инженерия знаний

Название этого раздела не совсем удачно, так как за термином Knowledge Engineering скрывается более широкая область науки, которая касается проблем, связанных с представлением, преобразованием и пополнением знаний. - Прим. ред.

Описанный метод позволяет анализировать достаточно сложные сцены определенного типа. Однако анализ сцен, проводимый человеком, отличается несравненно большей сложностью и включает информацию многих видов, поступающую от разнообразных источников.

Для восприятия окружающего трехмерного мира (по крайней мере близко расположенных объектов) человек располагает бинокулярным зрением (способностью к объемному восприятию предметов), обусловленным наличием двух глаз. Бинокулярное зрение, конечно, оказывается бесполезным при интерпретации двумерного изображения сцены. Но поскольку люди справляются с такой интерпретацией достаточно легко, по-видимому, процесс зрительного восприятия человека таит в себе много "скрытых возможностей".

В процессе анализа, безусловно, используется информация, "скрытая" в тенях, отбрасываемых предметами, и в различиях степени освещенности поверхностей предметов. Именно по этой причине некоторые из разумно сделанных штриховок поверхностей на рисунках (подобных изображенным на рис. 21-23) могут оказать существенную помощь в интерпретации.

Маленький человечек, изображенный на приведенных рисунках, иллюстрирует еще одно обстоятельство. А именно то, что в анализе преимущество отводится таким интерпретациям, которые согласуются с имеющимися у нас знаниями относительно гравитации и других физических законов. В соответствии с этим мы отдаем предпочтение таким интерпретациям, в которых предметы находятся на опоре, а не парят в воздухе.

К тому же нам обычно что-то известно о типах объектов, которые могут нам встретиться, и об их пространственных соотношениях. Общую идею здесь можно выразить такими словами: "Если мы узнали ногу, то мы знаем, где искать стопу". На самом деле, как указывал Макс Клюс, такая формулировка упрощает реальную ситуацию. Точнее было бы сказать так: "Если мы предварительно идентифицировали в определенном взаимоотношении ногу и стопу, соответствующим образом расположенные относительно других окончательно или временно опознанных объектов, то в таком случае мы можем с большой степенью уверенности идентифицировать эту комбинацию как нижнюю конечность".

Работы в области искусственного интеллекта преимущественно связаны с интерпретацией знания, полученного самыми различными путями и имеющего самые различные свойства. Термин инженерия знаний обычно относится к тем исследованиям в области искусственного интеллекта, в которых выделяется этот аспект.

Макс Клюс считал, что проблемы инженерии знаний наиболее целесообразно изучать в контексте зрительного восприятия. Другие исследователи сосредоточили внимание на распознавании речи, где также используются самые различные типы знаний.

Клюс поставил перед собой задачу написать такую программу для вычислительной машины, которая должна воспринимать на входе различные изображения игрушечной фигурки типа той, что показана на рис. 25. Эта фигурка может находиться в разных положениях, и программа должна найти способ применения информации об ограничениях, которые накладывают на положение фигурки физические законы. Исходя из этой информации, программа должна интерпретировать входное изображение (с учетом теней и плоскости опоры фигурки), давая в результате описание положения фигурки.

Рис. 25. Изображение фигурки, использованной Клюсом для изучения проблем анализа сцен

При распознавании речи также возникает необходимость в комбинации многих типов знаний, хотя и более сложным образом. Первоначально, как предполагалось, исследования по распознаванию речи должны были развиваться, усложняясь от распознавания фонем к распознаванию слов, а затем - с использованием правил синтаксиса - к распознаванию предложений и, наконец, к пониманию смысла всего текста.

В действительности все оказалось значительно сложнее. На распознавание фонем влияет промежуточное распознавание слов и смысла, на распознавании слов сказываются семантические и синтаксические соображения. Как будет видно из следующей главы, извлечение смысла требует непрерывного взаимодействия семантического и синтаксического анализов.

На анализ речи влияют также признаки, связанные с модуляцией голоса говорящего как по высоте, так и по громкости. Если мы можем видеть говорящего, то необходимую для распознавания информацию нам дают также его жестикуляция и мимика. Процесс распознавания зависит также от акцента и других характеристик, в частности от условий реверберации. Один из проектов системы распознавания речи основывался на использовании массива мини-компьютеров для параллельного анализа различных особенностей речи, причем выходы этих миникомпьютеров должны были объединяться в центральной вычислительной машине.

Синтаксис и распознавание образов

В любом процессе распознавания требуется определенное представление классов объектов, подлежащих распознаванию. Там, где приемлемо совмещение с эталоном, берется представление в форме эталонов. Во многих приложениях возможны различные варианты для образов, относящихся к одному классу, и часто весьма трудно сформулировать требования к задаче их распознавания.

Необходимо найти такую форму представления, которая указывает, что же является инвариантом для различных примеров, относящихся к одному классу. Даже в рамках относительно простой задачи распознавания символов, написанных от руки печатными буквами, нелегко сказать, в чем заключается инвариант, общий, скажем, для всех примеров написания буквы А. Классификация остается неизменной при умеренных искажениях - типа тех, что возникают, если букву написать на резиновой пленке и слегка растягивать ее в разных направлениях. Но классификация также остается неизменной, если на букву нанести какие-то дополнительные линии (предположим, как на рис. 26) или если приделать к некоторым линиям небольшие хвостики.

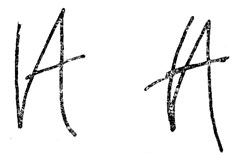
Рис. 26. Примеры искаженного написания буквы 'А'

Идеально класс должен быть представлен достаточно общим способом, который позволяет охватить все допустимые вариации, но вместе с тем сохраняет возможность отличить один класс от другого. Обычное описание (скажем, такое: заглавная буква А состоит из двух исходящих из одной точки (вверху) линий, раздвинутых внизу, с поперечной линией где-то посередине) часто оказывается лучше других представлений, так как хорошо удовлетворяет данному требованию.

Поэтому вполне естественно, что при решении проблемы распознавания зрительных образов делаются попытки использовать лингвистические методы. В приложении 3 к гл. 13 приводятся формальные методы работы с синтаксисом; там даны множества продукций, или правил переписывания, которые определяют предложение и простое арифметическое выражение.

Общий подход при синтаксическом представлении изображений состоит в том, что образы (классы) должны быть заданы наборами правил продукций. При этом необходимо, чтобы образы строились путем объединения малых фрагментов, но чтобы при этом можно было выделить некоторую элементарную составляющую. Такими элементарными составляющими могут быть, например, отрезки прямых фиксированной длины.

Предположим, что для представления отрезков прямых стандартной длины используются буквы а, b, с и d: отрезок а нарисован идущим слева направо, b идет вертикально снизу вверх, с - справа налево, a d - вертикально сверху вниз. Тогда прямоугольник, изображенный на рис. 27, начиная с его нижнего левого угла и двигаясь против часовой стрелки, можно представить в виде aaabbcccdd. Здесь используется соглашение о том, что последовательность символов соответствует соединению концов отрезков линии. Общее выражение для прямоугольника имеет вид

где n и m - положительные целые числа.

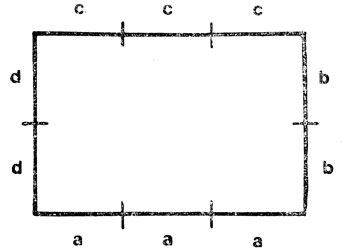
Рис. 27. Прямоугольник, который требуется представить синтаксически

Хотя форма Бекуса - Наура (см. Приложение 3 к гл. 13) допускает неограниченное повторение, в ней нельзя сделать так, чтобы символ а повторялся столько же раз, сколько и с, a b - столько, сколько d. Однако в распознавании зрительных образов могут использоваться и другие варианты формального синтаксиса (см. обзор Фу [3]).

Персептрон

Термин персептрон предложил в 50-х годах Франк Розенблат для некоторого класса систем распознавания образов, способных обучаться на опыте. Первое время эта идея вызывала большой интерес (не обошлось, правда, и без критики со стороны исследователей, работавших в других направлениях, - которые считали, что Розенблат переоценил значение своей идеи и незаслуженно получил слишком большую долю ассигнований, отпущенных на научные исследования).

Персептрон относится к более старому поколению систем распознавания образов в том смысле, что в нем предполагается, что распознаваемый образ изолирован. Этот и другие недостатки персептрона проанализированы в книге Минского и Пейперта [1], которая во многом способствовала изменению в направлении исследований, связанных с распознаванием образов.

Персептрон состоит из пороговых элементов, предназначенных для моделирования работы нервных клеток, как это первоначально предполагалось Маккалоком и Питтсом [4]. Некоторые характеристики таких модельных нейронов регулировались в ходе обучения. Несмотря на свои недостатки, сам принцип персептрона представляет интерес, поскольку алгоритм обучения персептрона, использованный для регулировки, может стать частью более совершенной системы обучения. К тому же в то время, когда была высказана идея персептрона, она представляла собой нечто достаточно определенное, что выкристаллизовалось из огромной массы весьма расплывчатых и разрозненных соображений относительно саморегулировки нейроноподобных элементов. (Однако не следует думать, что в персептроне было подытожено все ценное, что имелось в предшествующих исследованиях.)

Персептрон обычно описывается как схема для распознавания зрительных образов, но его можно использовать и в других сенсорных модальностях. При включении в схему устройств для частотного анализа и создания временных задержек (эквивалентных рисованию спектрограммы) она пригодна, например, для распознавания слов.

Как показано на рис. 28, персептрон содержит узлы трех типов. Сенсорные, или с-узлы, имитируют светочувствительные клетки сетчатки глаза. Они соответствуют демонам изображения, или демонам данных пандемониума Селфриджа. Обычно предполагается, что с-узлы являются элементами типа "все или ничего", но это не обязательно.

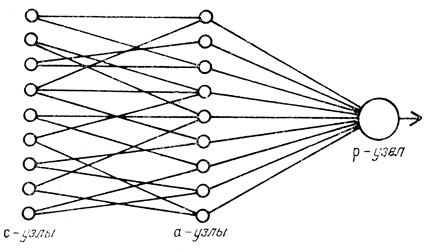
Рис. 28. Простой персептрон

Следующий слой узлов состоит из ассоциативных, или а-узлов, которые в общих чертах соответствуют вычислительным демонам пандемониума, В стандартном персептроне соединения от с-узлов формируются случайным образом еще в процессе конструирования системы, поэтому они определяют некоторые случайные "свойства" изображения. Роберте [5] рассмотрел вариант персептрона, в котором вычисляются данные о ценности каждого а-узла подобно тому, как это делается в пандемониуме. Входные соединения а-узла, ценность которого спустя какое-то время работы оказывается малой, аннулируются, после чего случайным (или псевдослучайным, см. Приложение 2 к гл. 1) образом устанавливается новый набор соединений.

Выходы а-узлов соединены с узлами реакции, или р-узлами, соответствующими демонам понимания пандемониума. Обычно при обсуждении принципов работы персептрона рассматривают лишь один р-узел, обосновывая это тем, что если возможно распознавание для одной категории, то аналогично можно поступить и с другими. Считается, что каждый из р-узлов дает ответ "да" или "нет", так что отпадает необходимость в чем-то подобном демону решений для окончательного выбора между ответами.

В одной из своих первых работ Маккалок и Питтс обсуждали типы вычислений, которые могли бы происходить в нервной системе. Они ввели представление о "модельном нейроне", свойства которого в общих чертах соответствуют свойствам нейронов живого организма. "Модельный нейрон" представляет собой пороговый элемент. У него имеется ряд входов, каждый из которых в данный момент может быть либо активным, либо неактивным, (Это соответствует правилу "все или ничего", по-видимому характерному для поведения нейронов.) Одни из входов модельного нейрона оказывают возбуждающее воздействие, другие - тормозящее. Каждый модельный нейрон имеет свое определенное значение порога, и если число активных возбужденных входов в какой-то момент времени превосходит порог и ни один из тормозящих нейронов в тот момент не является активным, то нейрон "срабатывает" и дает выходной сигнал.

На рис. 29 изображены два представления модельных нейронов. Иногда их рисуют так, что они по форме напоминают реальные нейроны, а иногда изображают просто кружочками. В любом случае возбуждающий вход заканчивается утолщением или треугольником, а тормозящий вход рисуется в виде маленького кружочка. От каждого нейрона отходит отросток, соответствующий аксону реального нейрона. Внутри изображения нейрона может записываться число, показывающее значение порога. На рис. 30 показаны модели нейрона, вычисляющие логические функции и, или и нет.

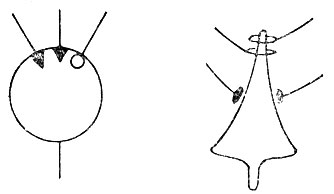
Рис. 29. Представления модельных нейронов

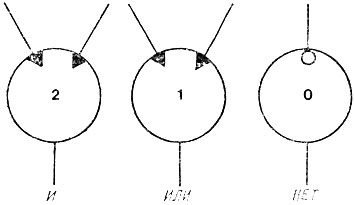
Рис. 30. Модельные нейроны, вычисляющие логические функции

При моделировании некоторых сторон активности нервной системы в искусственных системах часто допускается небольшое отступление от модели Маккалока - Питтса. В последней ведется простой подсчет числа возбужденных активных входов. Известно, что одним из механизмов обучения в нервной системе является модификация синапсов - точек, в которых аксон одного нейрона может воздействовать на другой нейрон. Этот эффект можно смоделировать, допустив, что с каждым синапсом связано определенное значение веса. Тогда вместо простого подсчета числа активных возбуждающих синапсов следует производить суммирование их весов.

Можно предположить, что тормозящие синапсы имеют отрицательные веса, и их следует учитывать при суммировании. Это противоречит первоначальной идее Маккалока и Питтса, которые предоставили тормозящим синапсам абсолютное право вето, однако удобнее считать все синапсы равноправными. При таких новых предположениях условием срабатывания нейрона и возникновения выходного сигнала является выполнение следующего неравенства:

где суммирование производится по всем входам данного нейрона, w_i - вес i-го синапса, t - порог, a x_i принимает значение 1 или 0 в зависимости от того, активен или неактивен i-й вход.

Как а-узлы, так и р-узлы персептрона служат моделями нейрона с учетом такого изменения. Некоторые из соединений между с-узлами и а-узлами являются возбуждающими, а некоторые - тормозящими. Веса синапсов, идущих к р-узлам, изменяются в процессе обучения, который называется алгоритмом обучения персептрона.

Чтобы алгоритм обучения мог работать, необходимо, чтобы каждый выход, или "догадка", персептрона сопровождался указанием от "учителя", верен ли этот выход. Тогда обычный вариант алгоритма обучения действует следующим образом.

Если реакция р-узла является правильной (т. е. если он срабатывает, когда образ принадлежит к распознаваемому классу, или если он не срабатывает, когда образ не принадлежит указанному классу), то веса не изменяются. Если р-узел не срабатывает, хотя распознаваемый образ на самом деле относится к рассматриваемому классу, то веса синапсов, бывших активными, увеличиваются на величину с. С другой стороны, если р-узел срабатывает на образ, который не принадлежит к распознаваемому классу, то веса активных синапсов уменьшаются на величину с.

Возможности персептрона были всесторонне исследованы математически. Теперь так называемую теорему сходимости по праву можно считать одной из "самых доказанных теорем", поскольку было предложено множество вариантов ее доказательства. Два из них, наиболее отвечающие существу дела, были отобраны Нильсоном [6]. Грубо говоря, теорема сходимости утверждает следующее: если существует множество значений весов, которые обеспечивают конкретное различение образов, то в конечном счете алгоритм обучения приводит либо к этому множеству, либо к эквивалентному ему множеству, такому, что данное различение будет достигнуто.

Чтобы строго сформулировать эту теорему, необходимо указать условия, которым должна удовлетворять последовательность входных образов. Она должна содержать выборки из конечного числа возможностей, часть которых принадлежит, а часть не принадлежит распознаваемому классу. Метод генерации последовательности должен быть таким, чтобы число предъявлений каждого образа из множества было неограниченным, причем каждый образ мог бы появляться неограниченно часто в неограниченно длинной последовательности.

Иногда теорему сходимости расценивают как окончательное подтверждение справедливости принципа персептрона, однако на самом деле она оставляет без ответа многие важные вопросы. Прежде всего она ничего не говорит о том, какие именно различия могут быть выявлены, - в формулировке теоремы этот вопрос полностью обходится. Минский и Пейперт показали, что самые серьезные ограничения наложены на типы различий, которые могут быть реализованы простым персептроном. (Система, описанная нами, является простым персептроном. Розенблат дал достаточно расплывчатое определение персептрона, поэтому нелегко точно сказать, какие схемы можно, а какие нельзя рассматривать как персептроны.) Сегодня уже не воспринимаются всерьез предположения, высказанные в первых работах по персептронам, согласно которым такие системы способны обучаться на опыте учитывать абстрактные соображения инвариантности образов при изменении их масштаба, переносе и вращении^*.

^* (Одно время возлагали надежды на многослойные персептроны, состоящие из нескольких слоев нейронов. Но исследование показало, что их возможности ненамного больше, чем у простых однослойных персептронов. - Прим. ред.)

Минский и Пейперт также указали, что теорема сходимости лишь гарантирует сходимость, но ничего не говорит о числе предъявлений, необходимом для этого, или о том, что для достижения окончательного результата, возможно, потребуется исключительно тонкая подгонка значений весов.

Тем не менее принцип персептрона весьма полезен для программиста как метод построения классификаторов, обучающихся с помощью "учителя". Такого рода ситуация складывается в системе распознавания произнесенных слов из небольшого словаря, работающей в условиях, когда при заданных входных сигналах можно подогнать систему под характеристики конкретного говорящего лица.