13. Достигнутые результаты [1985 Эндрю А. - Искусственный интеллект]

Работы в области искусственного интеллекта находятся в центре современных исследований в вычислительной технике. Этому вряд ли стоит удивляться, если вспомнить, что мы говорили в гл. 1 о существе проблемы искусственного интеллекта. Если считать, что она сводится к поиску способов заставить машины производить операции, сегодня ей недоступные, то искусственный интеллект по определению представляет собой передний край таких исследований. Поэтому проблема искусственного интеллекта привлекает многих способных людей, которые занимаются разработкой новых, все более совершенных вычислительных приемов.

Обработка списков, рекурсивная техника и использование формального синтаксиса - эти три предмета, относящиеся к области вычислительных наук, непосредственно связаны с искусственным интеллектом.

Обработка списков

Во многих задачах, связанных с искусственным интеллектом, приходится оперировать информацией, представленной не в числовой, а в символьной форме. Это, например, необходимо при составлении программ для автоматизированной математики, манипулирующих алгебраическими выражениями. Эти выражения представляют собой последовательности, или списки символов, причем слово список, по существу, используется здесь в его повседневном смысле, как список покупок, список участников какого-то мероприятия и т. д. Список в вычислительном смысле всегда является упорядоченным списком. Список покупок представляет собой упорядоченный список, если он записан, скажем, на листе бумаги в строгом порядке сверху вниз, однако при пользовании списком покупок такой порядок не имеет принципиального значения: подобный список можно было бы расположить и на отдельных листочках бумаги.

Простой список символов может быть представлен в памяти вычислительной машины стандартными методами: он подобен массиву числовых величин и его можно хранить в последовательных ячейках линейно упорядоченного пространства памяти вычислительной машины. Но если в ходе вычислений список требуется изменять, то простая, линейная, форма хранения не обеспечивает необходимой гибкости. Совершенно очевидно, что неудобно вставлять новые символы в середину линейного списка или стирать имеющиеся там символы. Кроме того, чтобы зарезервировать достаточный объем памяти, необходимо заранее знать длину списка.

Если же последовательные символы списка не обязательно заносятся в последовательные позиции памяти вычислительной машины, то список можно хранить в форме более удобной для манипулирования. Один из способов достижения такой гибкости состоит в том, что каждый символ хранится в определенном элементе списка, состоящем из одного или более машинных слов и содержащем две части. Сам символ представлен в одной из этих частей (по традиции называемой CAR); другая часть (называемая CDR) указывает адрес следующего элемента списка в последовательности, соответствующей нашему списку. Список, представленный в виде такой "цепочки", свободен от многих ограничений, свойственных списку, хранящемуся в виде числового массива. Вставить какой-либо элемент в середину "цепочки" можно просто путем модификации CDR элемента, расположенного непосредственно перед точкой вставки. Этот CDR в свою очередь должен указывать на новый элемент, вставляемый в список, a CDR нового элемента должен быть копией прежнего содержания CDR предыдущего элемента^*.

^* (Такая организация списков обсуждалась очень давно; см. например, книгу: Китов А. И. Программирование информационно-логических задач. - М.: Советское радио, 1967, ч. III, "Ассоциативное программирование". - Прим. ред.)

Термин обработка списков обычно относится к представлению и манипулированию списками в форме цепочки. До сих пор мы говорили только о простых линейных цепочках. Но списки становятся много полезнее, если часть CAR какого-то элемента списка может быть использована не только для представления символа, но и для указания на некоторыми подсписок. Тогда становится возможным представлять как простые линейные списки, так и структуры типа дерева.

После такого дополнения обработка списков превращается в способ представления вложенных структур и манипулирования ими удобным образом. Алгебраические выражения являются вложенными структурами, поскольку они могут состоять из подструктур, те - из подподструктур и так до любой глубины. Если нам понятно, что означает

то нам понятно и то, что получится, если один из символов, скажем а, заменить подвыражением

и т. д. Часть CAR элемента списка может представлять либо символ, такой, как а, либо указывать на начало подсписка, представляющего подвыражение типа (c + d). Трудно представить, как вложенные структуры можно было бы обрабатывать иначе, чем с помощью цепочечных списков.

Тот факт, что выражения естественного языка носят вложенный характер, еще более подчеркивает, насколько важно иметь возможность обрабатывать вложенные структуры. Слово в предложении (существительное или прилагательное) можно заменить именным или определительным оборотом либо целым предложением. Это предложение будет иметь такую же структуру, как и исходное, и слова в нем можно снова заменить оборотами и предложениями. В принципе глубина вложения ничем не ограничена, однако если в предложении имеются два или три уровня вложения, то люди с ним уже не в состоянии работать.

В области искусственного интеллекта был разработан ряд специальных языков для обработки списков. Наиболее известен из них язык ЛИСП (LISP - сокращение от LISt Processing language, что означает "язык для обработки списков") [1], созданный Маккарти в 50-х годах. То обстоятельство, что этот язык до сих пор находит широкое применение, говорит о том, что он удовлетворяет основным требованиям. Этот язык не только широко используется сам по себе, но и оказал воздействие на построение таких языков программирования, как АЛГОЛ-68, ПАСКАЛЬ и ПЛ-1.

Новые языки типа АЛГОЛ (ПАСКАЛЬ и АЛГОЛ-68) отличаются от более старого языка АЛГОЛ-60 именно тем, что позволяют достаточно удобным образом обрабатывать списки. Некоторые дополнительные соображения относительно обработки списков содержатся в приложении 1 к настоящей главе.

Рекурсия

При обсуждении вложенных структур целесообразно остановиться на понятии рекурсия. Алгебраические выражения естественным образом являются рекурсивными, поскольку любое выражение - что бы ни понималось под ним - может войти как подвыражение в другое алгебраическое выражение. Методы, используемые при обработке списков, должны быть рекурсивными. Это означает, что при работе с внешней структурой (например, с внешним алгебраическим выражением) мы должны располагать возможностью на каком-то этапе прервать работу и применить используемый метод во всей его полноте к некоторому подвыражению. Закончив работу с подвыражением, необходимо иметь возможность возобновить обработку внешнего выражения с того места, где она была прервана. Конечно, при работе с подвыражением также может возникнуть необходимость в рекурсивной обработке подподвыражения и т. д.

Некоторые дополнительные замечания о рекурсии сделаны в приложении 2 к этой главе. В настоящее время рекурсия стала привычной характеристикой разнообразных аспектов программирования на ЭВМ. Возможность создания рекурсивных процедур и возможность рекурсивного вызова процедур были предусмотрены в языке АЛГОЛ с самого начала его создания. (Метод рекурсии часто кажется ненужным, когда языки программирования используются для обычной числовой обработки, однако он представляет ценность в других приложениях, особенно при обработке символьных текстов.) Программы, записанные на языке АЛГОЛ, сами по себе являются вложенными структурами, и используемые для их перевода на машинный язык компиляторы должны оперировать с рекурсивными структурами.

Ценность метода рекурсии стала очевидной в связи с работами в области искусственного интеллекта. Повседневное поведение человека и используемые им способы решения задачи носят рекурсивный характер. Когда человек берется за решение какой-то задачи (допустим, за написание статьи), он должен быть в состоянии прервать эту работу и применить те же методы решения задач и планирования к той или иной подзадаче. Примерами подзадач могут быть, скажем, приготовление кофе для поддержания сил, получение необходимой информации в библиотеке, покупка писчей бумаги, чернил и т. д. Эти подзадачи в свою очередь могут включать в себя другие подподзадачи, как-то: добывание денег для покупки бумаги, организация поездки в библиотеку или в магазин канцелярских товаров и т. д. По завершении решения каждой подзадачи возобновляется работа над исходной задачей и, возможно, человек говорит: "Итак, где я был?"

Рекурсивный характер планирования и решения задач человеком был перенесен в такие программы искусственного интеллекта, как универсальный решатель задач Ньюэлла, Шоу и Саймона (гл. 2 и 3). Рекурсия стала важной характеристикой специальных языков программирования, разработанных для решения задач искусственного интеллекта (в частности, для языка ЛИСП, о котором мы уже говорили).

Формальный синтаксис

Были разработаны специальные средства для представления синтаксиса, т. е. грамматических правил языка формальным и однозначным образом. Правила разработанного типа могут подаваться в вычислительную машину в качестве входной информации. Программа использует эти правила для определения процесса перевода или же выводит из них эквивалентное множество правил, удовлетворяющее требованиям, которым исходное множество не удовлетворяет.

Как мы уже отмечали в гл. 9, для перевода или анализа смысла естественно-языковой информации одних синтаксических соображений недостаточно. Формальный синтаксис главным образом применяется в связи с машинными языками и при теоретическом рассмотрении лингвистами естественного языка. Наиболее известным формализмом для описания правил синтаксиса является форма Бекуса - Наура (БНФ), названная так по имени двух исследователей, которые ее разработали и первыми использовали. Первая публикация [2], принесшая методу БНФ широкую известность, была посвящена использованию этого метода для определения языка АЛГОЛ-60.

Общее представление о формальном синтаксисе сложилось в связи с исследованиями по естественному языку, проведенными лингвистом Хомским. Эти исследования он проводил в Массачусетском технологическом институте (США), где в то время осуществлялась работа по автоматическому переводу и системам вопрос - ответ. Очевидно, формальный синтаксис можно рассматривать как своего рода отход от исследований по искусственному интеллекту^*.

^* (Говоря более точно, формальные системы, примером которых могут служить формальные грамматики, предложенные Хомским, составляют лишь часть, того, что охватывается термином "искусственный интеллект". - Прим. ред.)

Психология

Одним из побудительных мотивов исследований в области искусственного интеллекта является стремление понять сущность процессов мышления у человека. Отношение психологов к проблеме искусственного интеллекта и степени его "родства" с интеллектом естественным колеблется в широких пределах - от пренебрежительного скептицизма до безудержного энтузиазма. Работа Ньюэлла, Шоу и Саймона ставила своей прямой целью моделирование процессов решения задач человеком. Одним из энтузиастов применения методов искусственного интеллекта в психологии по праву считается Аптер [3].

Скептики заявляют, что исследователи, работающие в области искусственного интеллекта, добиваются решения задач методами, которые имеют очень мало общего с методами, используемыми людьми. Разнообразие подходов, отличающее различные исследования в области искусственного интеллекта, говорит о том, что программы составлены с применением определенных наборов приемов, специально разработанных для каждой конкретной задачи.

В следующей главе мы покажем, что некоторые весьма важные стороны умственной деятельности человека не имитируются программами, написанными для вычислительных машин. Вместе с тем при решении различных задач люди, безусловно, прибегают к эвристикам (хотя в свете того определения эвристик, которое было дано в гл. 2, это звучит как тавтология), и исследования в области искусственного интеллекта позволили выявить кое-какие эвристики, которыми, возможно, пользуется человек. Исследования по искусственному интеллекту помогли также выделить некоторые важные аспекты процесса мышления, такие, например, как его рекурсивный характер.

Даже в тех случаях, когда соответствие между машинным методом и методом, применяемым человеком, кажется весьма сомнительным, анализ задачи в форме, приемлемой для искусственного интеллекта, позволяет лучше понять ее характер. По-видимому, это полезно как для разработки искусственного интеллекта, так и для понимания естественного.

К задачам такого рода относятся, в частности, распознание речи и анализ сцен, о которых мы говорили в гл. 8 (в разделе "Инженерия знаний"). В значительной степени прояснился также характер задачи понимания языка. До исследований в области искусственного интеллекта школьный "разбор" и "анализ" предложений считались алгоритмическими процедурами. Теперь же мы видим, сколь существенно они зависят от несинтаксических соображений. Исследования по искусственному интеллекту пробудили интерес к психолингвистике.

Специальные языки (ЛИСП и т. д.) и другие средства (ПЛЭННЕР, МИЦИН и пр.) из области искусственного интеллекта обеспечивают весьма "естественное" общение человека с машиной. Несмотря на свое несовершенство, методы хранения и представления информации, используемые в искусственном интеллекте, имеют важные аналогии с методами, используемыми человеком. К числу таких аналогий можно отнести рекурсию и ее применение к вложенным структурам. Существуют и другие "точки соприкосновения", которые менее ощутимы. Ценность методов искусственного интеллекта как моделей обработки информации человеком нелегко определить количественно, но, несомненно, она существенна.

Практические применения

Нет сомнения, что результаты, достигнутые в ряде областей искусственного интеллекта, находят практическое применение. В качестве примера можно назвать различные методы распознавания образов и распознавание речи. Роботы и экспертные системы создавались с ориентацией на практические приложения, и определенные результаты здесь имеются.

Дальнейшие достижения возможны на пути объединения этих новых систем. Сочетание системы распознавания речи с экспертной системой (и с системой синтеза речи, что осуществить сравнительно просто) откроет возможность консультаций с "экспертом" по телефону. Рассматриваются планы создания автоматической системы заказов билетов на самолеты. Кроме непосредственно заказа билета такая система будет в состоянии давать информацию о расписании движения самолетов и сможет предлагать маршруты путешествий. Она будет давать также информацию о наличии свободных мест^*.

^* (Такая система, названная СИРЕНА, уже несколько лет успешно действует в Москве. - Прим. ред.)

Как и многие другие научно-технические достижения, методы искусственного интеллекта могут служить не только прогрессу, но и целям уничтожения. В настоящее время много говорится о крылатых ракетах. Для их навигации используются методы распознавания образов. В гл. 15 мы коснемся морально-этических аспектов исследований в области искусственного интеллекта.

Приложение 1. Обработка списков

На рис. 43 показано, каким образом алгебраическое выражение

можно представить в форме древовидной структуры. Чтобы записать это выражение в памяти вычислительной машины, необходимо ввести в рассмотрение элементы обработки списков двух типов: соответствующие нетерминальным вершинам дерева и соответствующие его терминальным вершинам (или листьям). Элемент для нетерминальной вершины содержит оператор (+, -, × или ÷) и ссылки (или указатели) на два других элемента. Каждый элемент, соответствующий листу, содержит некоторое представление для символа х, а или b. На рис. 44 показано дерево с прямоугольниками, представляющими элементы списка.

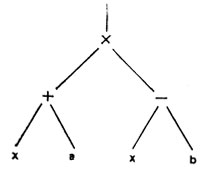
Рис. 43. Дерево, представляющее выражение (x + я)(x - b)

Рис. 43. Дерево, представляющее выражение (х + а) × (х - b)

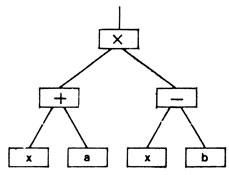
Рис. 44. Древовидная структура в памяти вычислительной машины

Теперь рассматриваются элементы списка, имеющие более двух составляющих частей (CAR и CDR), о которых говорилось ранее. Развитие идеи обработки списков приводит к более сложным элементам. Например, в языке АЛГОЛ-68 допускаются структуры, которые могут содержать ссылки на другие структуры и, следовательно, служить в качестве элементов списка. В языке ПАСКАЛЬ используются записи, которые могут содержать указатели на другие записи.

Процедура формального дифференцирования может выполняться на дереве, подобном тому, что показано на рис. 44, и создавать дерево, представляющее производную. Если эта процедура используется для работы на дереве, содержащем только одну терминальную вершину, то она должна создать дерево, содержащее одну вершину, причем эта вершина содержит символ "1", если исходная вершина содержала "х", и символ "0" - в противном случае. Для дифференцирования более сложных выражений процедура должна действовать в соответствии с правилами дифференцирования суммы, разности, произведения и т. д.:

где значок "штрих" означает дифференцирование.

Поскольку значки "штрих" стоят в правой стороне равенств, процедура дифференцирования должна быть рекурсивной. При генерации дерева, соответствующего производной (скажем, от суммы), процедура дифференцирования должна порождать структуру, содержащую поддеревья, которые представляют производные каждого из подвыражений этой суммы.

На рис. 45 показано дерево производной, которое такая процедура могла бы создать исходя из дерева, изображенного на рис. 44. Правило дифференцирования производной требует, чтобы в этой производной снова появились подвыражения оригинала. Нет необходимости создавать дубликаты деревьев. На рис. 45 дерево производной содержит ссылки на поддеревья исходного дерева, причем отсоединять их от исходного дерева не нужно. Таким образом, эти поддеревья служат двум целям.

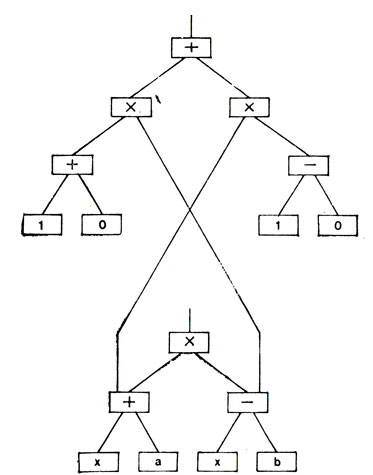
Рис. 45. Структура, представляющая производную по переменной х. В нижней части рисунка приведено исходное дерево, причем некоторые его части являются также частями дерева производной. Производная здесь представлена таким способом, который - хотя и правилен - приводит к слишком громоздкому дереву. В данном случае возможно автоматическое упрощение дерева производной

Приложение 2. Рекурсия

Приложение 1 показывает, что процедура для работы на вложенной структуре - например, для задачи формального дифференцирования - должна быть рекурсивной, если вложение имеет неопределенную глубину.

В качестве примера в литературе часто приводят рекурсивную процедуру для вычисления факториалов целых положительных чисел. (Факториал целого числа равен результату перемножения всех (разных) отличных от нуля положительных целых, не превышающих это число, причем по определению факториал нуля равен единице. Факториал обозначается восклицательным знаком, идущим после числа: например, факториал 6 записывается как 6!, и 6! = 1 × 2 × 3 × 4 × 5 × 6 = 720.)

В обозначениях языка АЛГОЛ-68 процедуру вычисления факториалов можно записать следующим образом:

Первая строка показывает, что процедура, называемая fact, воспринимает на входе целое число, которое в самой процедуре обозначено символом n; результат также равен целому числу. Слово FI (не является стандартным английским словом) используется в качестве закрывающей скобки, соответствующей if, а звездочкой обозначается умножение.

Вряд ли этот пример кого-то убедит в пользе рекурсии. Факториалы можно легко вычислять нерекурсивным методом, при этом предъявляется меньше требований к вычислительному времени и объему памяти. Однако рекурсивный способ представления информации обычно считают более "элегантным" и более понятным для людей, читающих программу. Разработаны методы автоматического перевода большого класса рекурсивных процедур в эквивалентные нерекурсивные процедуры. Рекурсивная форма более приемлема для людей, а нерекурсивная более эффективна при выполнении процедуры на вычислительной машине. Но эти методы неприменимы, если рекурсия действительно необходима, как, например, в случае вложенных структур не определенной заранее глубины, о которых мы говорили в приложении 1.

До сих пор мы рассматривали рекурсию, возникающую при декларации самой процедуры. Но рекурсия может возникать и при активации, или вызове, процедуры. Простым примером может служить процедура нахождения наибольшего из двух чисел:

Эту простую нерекурсивную процедуру можно использовать для присваивания значений следующим образом:

при этом возникает некоторая разновидность рекурсии, поскольку внешнее обращение к max не может быть завершено, пока не будут выполнены три внутренних обращения.

Баррон [4] указывает на "неудачную" функцию, называемую функцией Акермана, которая объединяет эти два вида рекурсии. Это функция двух переменных, скажем A(m, n), которая определяется следующим образом:

Баррон предлагает читателю - если у того найдется минут пять свободного времени - вычислить исходя из этого определения функцию A(2,3). (Однако признаюсь, что у меня эта процедура заняла больше пяти минут. Более того, при первой попытке я допустил ошибку.) Сложность этой задачи для человека вызывает у него чувство восхищения алголоподобными языками, позволяющими решать задачу "с ходу". Достаточно лишь следующим образом (в АЛГОЛЕ-68) определить процедуру:

Тогда значение A(2,3) будет напечатано в ответ на следующую команду:

Аналогично можно произвести вычисления и для других значений аргументов (но не слишком больших, чтобы не выходить за разумные пределы времени вычислений и объема памяти).

Приложение 3. Формальный синтаксис

Наиболее известной системой формального синтаксиса является, как мы уже отмечали, форма Бекуса - Наура (БНФ) в том виде, как она использовалась для определения языка АЛГОЛ-60 [2]. Чтобы отличить символы БНФ от символов АЛГОЛ-60 и любого языка, синтаксис которого необходимо определить, в БНФ используются довольно необычные символы. Один из них - это : : =, который означает "определяется как" или "может быть переписан как". Другой символ - вертикальная черта (|), используемая для разделения различных альтернативных возможностей. Кроме того, в БНФ имеются угловые скобки <и>. Символ, заключенный в угловые скобки, называется нетерминальным символом, так как он определяется одним из правил. Символы и цепочки из символов, не заключенные в скобки, являются терминальными символами и представляют лишь самих себя.

где (цифра) - нетерминальный символ, а каждая из цифр 0, 1, 2, 3, ..., 9 - терминальный символ.

Этот символизм становится намного более мощным, когда в правых частях определений допускается использование нетерминальных символов, и особенно в том случае, когда допускаются рекурсивные определения, так что определяемый объект может появиться с правой стороны своего собственного определения.

Строка из цифр, имеющая любую длину, начиная с единичной, определяется как цел. бзн. (сокращение для "целого без знака") одним из следующих соотношений:

Тогда целое, которое может иметь (а может и не иметь) знак, определяется так:

где символы "+" и "-" являются терминальными. Предположим, что слово пав (простое алгебраическое выражение) используется для указания на выражение, содержащее четыре операции +, -, × и ÷, причем выполняется обычное условие, что последние две операции имеют приоритет перед первыми. Тогда пав определяется следующим множеством правил:

Круглые скобки, охватывающие <пав> в правиле для <блок>, являются терминальными символами, показывающим, что пав в круглых скобках рассматривается как блок. Это определение является рекурсивным, поскольку <пав> появляется в правой части этого правила. Определение вложенной структуры должно быть рекурсивным.

Некоторый класс предложений английского языка определяется следующим образом:

Обычно такое множество правил используется с целью анализа входных цепочек символов (например, в программе АЛГОЛ-60), которые должны соответствовать тому, что определяется. Однако правила можно использовать вместе с генератором случайных чисел (см. гл. 1, приложение 2) для создания случайных предложений, подчиняющихся правилам этого множества. Можно сказать, что процедура анализа запускается в обратную сторону. Приведенные выше правила можно, например, использовать для построения известной фразы, которую часто используют для проверки пишущих машинок (с латинским шрифтом): "The quick brown fox jumps over the lazy dog", (Проворная коричневая лиса перепрыгнула через ленивую собаку.)

Чтобы построить какое-нибудь предложение, процесс генерации нужно запустить с правила 1. Здесь имеются две возможности, и для выбора какой-то одной из них следует обратиться к генератору псевдослучайных чисел. Если генерируется предложение "The quick brown fox...", то на первом шаге должна быть выбрана первая из этих двух возможностей.

В дальнейшем процесс генерирования должен развиваться в соответствии с выбранной альтернативной, т. е. если выбрана первая из возможностей, то управление сначала должно перейти к правилу 2 для создания "существ, часть", а после того, как это сделано, - к правилу 4 для создания "глагольн. часть". Поскольку правила 2 и 4 в свою очередь передают управление другим правилам, то необходимо иметь стек, или магазинную память, для напоминания о неоконченных моментах в различных правилах. Когда осуществляется первая передача управления от правила 1 к правилу 2, в стек помещается первый элемент и указатель - на следующий по порядку элемент (в соответствии с выбранной альтернативой). Если этот метод программируется на языке, допускающем использование рекурсивных процедур, то стек может быть составной частью реализующего правила языка, и тогда пользователю не обязательно нужно указывать его явным образом.

Если в процессе генерирования встречается терминальный символ, то он добавляется к выходной строке, которая создается.

Предложения, которые генерируются таким образом из приведенного множества правил, обычно очень короткие и неинтересные, что-то вроде "The brown cat runs" (коричневая кошка бежит) или "A mouse jumps a quick lazy dog" (мышь прыгает на быструю ленивую собаку). Словарь данного множества правил содержит 18 слов, выступающих в качестве терминальных символов: два артикля, четыре существительных, четыре прилагательных и т. д. Этот метод применим, однако, и к большим словарям, содержащим яркие, выразительные слова, - в этом случае рождались удивительные "современные" стихи. Они "современны" потому, что, во-первых, они таинственны и, во-вторых, в них абсолютно отсутствует рифма. Об этой разновидности "эстетической деятельности" машины мы говорили в гл. 11.