Кибернетические модели развития

Одна из немногих моделей развития как такового, которую можно считать кибернетической, - это выполненная в металле модель Голдейкра и Бина [1-5]. Она основана на предположении, что, "вероятно, развивающийся организм по существу непрерывно сам себя пристально изучает, и рост управляется своего рода "мозгоподобным" взаимодействием большинства или всех клеток организма" [6]. Под "мозгоподобным" взаимодействием здесь понимается нечто более специфическое, чем просто то, что существуют сложные комбинации потоков информации и взаимозависимостей; имеется в виду то, что элементы системы работают по типу да - нет и что вся информация кодируется одинаковыми дискретными импульсами. К сожалению, однако, нельзя сказать, чтобы эта гипотеза имела много подтверждений. Другая возможность, которую указывает сам Голдейкр [7], состоит в том, что сама нервная система, быть может, в какой-то мере управляет развитием (неясно, в какой мере Голдейкр хочет, чтобы его модели так интерпретировались), но это снова гипотеза, и тоже не очень-то подтверждающаяся. Кроме того, эта система используется как модель некоторых сторон деятельности мозга [3], которые мы здесь не будем описывать.

Эта модель, названная "электронный паттерн-генератор", состоит из большого числа электронных элементов или искусственных нейронов, из которых с помощью коммутатора можно составлять разные схемы. Так, их можно соединять наподобие разных "тканей", где каждый электронный элемент играет роль "клетки". В экспериментах использовалось большое число электронных элементов [2], причем каждый, получив импульс, после некоторой задержки посылал импульсы ко всем элементам, в данный момент с ним связанным. Временная задержка оказалась необходимой не только для того, чтобы легче было следить за прохождением импульсов, но и для того, чтобы элементы не запирались в положении "да" при образовании замкнутых циклов, что случалось, когда импульс приходил по циклу обратно к элементу, испустившему его, раньше, чем он кончал его испускать. Чтобы прохождение импульсов можно было наблюдать зрительно, при приходе импульса к электронному элементу на нем вспыхивала лампочка; из тех же соображений удобства в одном варианте модели все элементы при каждом приходе импульса издавали звук, каждый своей высоты.

Самый интересный результат, который Голдейкр и Бин получили в опытах с этой моделью, - это то, что они сумели получить асимметричную картину импульсов при симметричной схеме соединений; это интересно потому, что, как мы видели, одна из загадок развития - это как в однородной системе может возникнуть дифференцировка. Голдейкр и Бин нашли много способов соединения, при которых это получается. Самый простой из них следующий, причем, как мы видим, каждая клетка имеет две входные и две выходные связи:

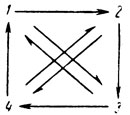
Оказывается, при таком соединении, если в любом месте системы дать импульс, то лампочка на одной клетке будет мигать, а на всех остальных клетках лампочки будут гореть все время. Далее, если пульсирующей клетке не дать пульсировать, то начнет пульсировать другая клетка, а если ей тоже не дать, то начнет пульсировать третья и так далее, пока не запретить всем клеткам пульсировать. Так, асимметрию можно "гонять" по всей системе.

Хотелось бы знать точно, почему так происходит, и даже в случае такой сравнительно простой ситуации Голдейкр и Бин затрудняются точно установить причину. В частности, хочется знать, определяется ли это начальной асимметрией, состоящей в том, что начальный импульс дается только в одной точке системы, или то же самое произошло бы и тогда, когда все четыре элемента получили бы импульсы одновременно.

Голдейкр [1] пишет дальше, что если устроить так, чтобы каждый элемент делился, получив определенное число импульсов, а это можно устроить в эксперименте, подключая в этом месте дополнительный элемент, - то мы увидим, какие после этого возникнут импульсы и, следовательно, где будет следующая точка роста. "Этот процесс можно продолжить неограниченно, и при этом видно, как таким образом, эпигенетически в растущем организме могут возникать определенные формы" [8]. Это открывает очень интересные возможности, которые Голдейкр, видимо, не успел еще сколько-нибудь подробно изучить. Поэтому остается только с огромным интересом ждать дальнейших работ на эту тему.

Голдейкр и Бин рассматривали также проблему самовоспроизведения. Они сообщают об аппарате, который может скопировать схему связей одной системы и закодировать ее в виде другой такой же системы. Бин называет это самовоспроизведением [2], каковым оно, конечно, не является, так как при этом происходит лишь удвоение системы с помощью другой, внешней системы.

Ближе к задачам развития замечание Голдейкра, что то, что он называет явлением "разрывности",- явление, состоящее в том, что в данной области соседние клетки становятся совсем разными, например одни клетки входят в состав волос, а другие остаются неизменными,- может быть объяснено на языке таких моделей, как у них, но трудно объяснимо, например, с помощью градиента диффузии.

Представляются возможными два основных способа интерпретации этих моделей. Можно рассматривать каждый элемент как клетку ткани; Голдейкр и Бин, видимо, так и делают. Можно также рассматривать каждый элемент как генетический; тогда начальную структуру модели можно будет рассматривать как одну клетку. Однако каждая из этих интерпретаций приводит к своим трудностям.

Если мы решим рассматривать каждый электронный элемент как клетку, то развитие модели будет начинаться не с одной клетки, а с какого-то их числа, организованного определенным образом, симметрично или как-то иначе. Так, минимум сложности, необходимый для развития (в отличие от простого роста или симметричного увеличения),-это четыре единицы, соединенные так, как показано выше. Но в действительности развитие начинается с одной клетки, и хотелось бы знать, как получилась схема, с которой начинает работать модель. Более того, эта схема развивается только одним определенным образом. Следовательно, чтобы развитие дало и другие структуры, оно должно начинаться с еще более сложных систем связей. Развитие таких систем, состоящих из простейших единиц, должно полностью определяться системой связей. Можно было бы поступить иначе: сделать эти элементы более сложными - биологическая клетка ведь сложна и несет большое число генов или инструкций - и начать с меньшего числа клеток. Идеально было бы начинать с инструкций, даваемых лишь одной клетке - зиготе, и это мы и пытаемся делать в следующих главах. Конечно, интересно посмотреть, что может получиться при развитии из систем, составленных из простых триггеров, но, быть может, не нужно такое ограничение в исследовании биологического развития. Точно так же нет необходимости и в ограничении передачи информации от клетки к клетке к одним только одинаковым возбуждающим импульсам ввиду сложности межклеточных взаимодействий, особенно химических, в реальных организмах. Лучше было бы потребовать, чтобы развитие начиналось с одной клетки, и затем искать минимальное число инструкций, которые надо было бы ей Дать, чтобы получить различные схемы развития. В гл. 5 мы будем заниматься моделями, в которых единицы имеют N состояний и могут посылать друг другу два типа сигналов; и даже в этом случае при таком ограничении на передачу информации, как мы увидим, можно будет подучить не все формы развития.

Второй способ интерпретации модели Голдейкра и Бина, при которой каждая электронная единица рассматривается как своего рода генетическая, а исходное состояние модели - как набор генетических компонент, определенным образом соединенных, тоже неудовлетворителен. Существуют некоторые данные, говорящие о том, что гены могут взаимодействовать (см. приложение 4 о работе Жакоба и Моно), но трудно придумать истолкование той асимметрии в работе, которой обладает модель, особенно если учесть, что бессмысленно считать, что ген, получив определенное число сигналов, в одиночку делится. Во всяком случае, при теперешнем уровне этого исследования проблема образования структуры в целом организме, существенно связанная с развитием, остается незамеченной.

Тем не менее эта работа все-таки представляет собой полезный начальный подход к сложным проблемам развития. Поскольку исследование моделей других двух родов, т. е. в виде программ и просто на бумаге, излагаемое в следующих главах, имеет столь же предварительный и поисковый характер, то его можно рассматривать как дополнение к исследованиям Голдейкра и Бина.

Иначе подошел к этой проблеме Улам [9], который исследовал, какие пространственные расположения можно построить непрерывным применением к начальному положению какого-либо простого правила. Например, он полагал, что на бесконечном листе клетчатой бумаги действует такое правило: "Если задано множество квадратиков, принадлежащих n-му поколению, то (n + 1)-му поколению будут принадлежать все соседние с ними с одной только оговоркой: те, которые соседствуют более чем с одним квадратиком n-го поколения, не рассматриваются^* [10]. Можно начать с одного квадратика; тогда получится последовательность поколений квадратиков, из которых ни один не имеет больше двух соседей. Рассматривается несколько более сложных правил, в том числе такие, при которых прежние поколения могут стираться; эти правила применяются и к другим разбиениям плоскости: на треугольники и на шестиугольники. По сути самого подхода неожиданных результатов тут нет, и, конечно, все картинки симметричны. Быть может, самый интересный результат - это то, как быстро получается сложная фигура, если начальная фигура - шестиугольник.

^* (И не берутся также квадратики, принадлежащие предыдущим поколениям.- Прим. перев.)

Улам также поднимает в общем виде проблему о том, как предсказать характер роста, если каждый элемент имеет определенный тип, отличный от типа его предшественника и существенно зависящий от типов по меньшей мере двух элементов прошлого поколения. Например, элементами можно считать не треугольники, а их вершины. Теперь пусть у нас вначале был один треугольник, с трех его сторон образуются три новых треугольника, и пусть в каждом новом треугольнике тип дальней вершины как-то определяется типами двух его вершин, принадлежащих той его стороне, на которой он образован. Тогда, если образование новых треугольников продолжается таким же образом, то возникает вопрос, как предсказать типы вершин в очень далеких поколениях. Улам пишет, что даст решение задач этого типа в одной из следующих работ.

Улам упоминает также, что его модели программировались на вычислительной машине: очень интересно было бы узнать, как это делалось, поскольку программирование пространственных моделей более трудоемко, чем в линейном случае (гл. 5).

Маруяма построил модель, очень похожую на модели Улама, но в которой начальная фигура представляет собой несколько несоединенных друг с другом квадратиков. Эту модель мы опишем в гл. 8 (раздел "Развитие, приводящее к сложности"), к содержанию которой она наиболее близка.

Еще одна модель, на которую следует здесь указать, описана в работе Тьюринга "Химические основы морфогенеза" [11]. В этой работе Тьюринг показывает, как в совершенно однородной системе может возникать весьма правильная структура, при условии, что эта система неустойчива и в определенное время подвергается случайному воздействию. Для простоты он берет двумерный кусок ткани, свернутый в баранку, чтобы не иметь дела с граничными эффектами. Берутся два (и для простоты только два) химических вещества, которые диффундируют по этой ткани и реагируют друг с другом, воспроизводясь или уничтожаясь при этом. Утверждается, что система приходит в равновесие и оба вещества равномерно распределяются по ткани. Далее Тьюринг берет специальные графики скоростей диффузии и реакции и показывает (для чего ему требуются машинные просчеты), что в некоторых случаях, если одно вещество в некотором месте оказалось в слишком высокой концентрации, то эта концентрация будет еще увеличиваться и из каждого такого места вещество будет растекаться, так что область высокой концентрации будет расти. Далее он показывает, что при некоторых условиях по всей системе может пойти волна высокой и низкой концентрации этого вещества, длина которой зависит от графиков скоростей диффузии и реакции. Тем самым возникает какой-то порядок, могущий лежать в основе формирования биологических структур.

Как указал Уоддингтон [12], главный недостаток этой модели состоит в том, что параметры возникающей структуры не зависят от размеров всей системы. То есть если бы система была больше, параметры, определяющие структуру, остались бы теми же самыми, возросло бы число элементов, составляющих эту структуру. Поэтому, в то время как относительно внешние эффекты, например пятнистая окраска крыльев насекомых, хорошо этой моделью объясняются, она никоим образом не объясняет возникновения таких структур, какие нужны для формирования органов при развитии.

Уделила внимание росту и развитию и кибернетическая по своей сути организация под названием "Исследовательская группа Арторга" [13]. Это клуб денежных вложений, вклад которого в изучение развития - необычная идея использовать себя как экспериментальную модель (Artorga - сокращение от Artificial organism - искусственный организм) с целью найти условия успешного роста системы. Показателем успеха организации считается прибыль, но более основным критерием успеха является выживание системы. В частности, члены этой организации, среди которых много ученых и много кибернетиков, пишут информационные статьи, которые рассылаются всем членам организации. Большинство этих статей теоретические, и многие из них уже были весьма полезны. (На некоторые из них мы ссылаемся в этой книге.) Надо сказать тем не менее, что никакого развития этой системы в каком бы то ни было смысле пока незаметно; прибыль, приносимая денежными вкладами, невелика, а статьи обнаруживают мало общего между собой - происходит их накопление, но едва ли объединение.