Модели самовоспроизведения

В большинстве организмов воспроизведение клеток и развитие тесно связаны. В области самовоспроизведения в кибернетике теперь имеется значительное количество работ, и поэтому мы бросим взгляд на некоторые из них в надежде на то, что они прольют свет на проблему развития. Обзор Эдварда Ф. Мура "Машинные модели самовоспроизведения" [14] покрывает большинство из них. В нем имеется полная библиография, поэтому мы не будем давать ссылок на работы по этой теме, а отсылаем за ними к статье Мура.

Честь быть инициатором этого направления принадлежит Джону фон Нейману, предпринявшему две различные и важные попытки решения этой проблемы. К сожалению, .большинство его работ на эту тему, как и большинство работ Тьюринга, до сих пор не опубликовано, хотя и предполагается их опубликовать^*. Мы располагаем, однако, его работой "Общая и логическая теория автоматов" [15]; существуют также ротапринтные издания нескольких его статей по самовоспроизведению [16, 17]. Кроме того, имеется статья Кемени с описанием другого подхода [18].

^* (Работы фон Неймана по самовоспроизводящимся автоматам изданы отдельной книгой: "Theory of self-Reproducing Automata by John von Neumann", edited and completed by Arthur W. Burks. University of JUinois Press. Urbana and London, 1966. В настоящее время готовится ее русский перевод в издательстве "Мир".- Прим. ред.)

Первый подход, описанный в классической статье "Общая и логическая теория автоматов", представляет собой развитие работы Тьюринга о бесконечных автоматах (см. приложение 3), в котором показывается, как можно сделать такой автомат самовоспроизводящимся. Это делается следующим образом:

1. Если описание машины А заложить в универсальный автомат (то есть в универсальную машину Тьюринга), то выходом полученного автомата В будет поведение машины А.
2. Если поведение машины А состоит не в печатании на ленту, а в последовательности действий, необходимых для построения машины С, то выходом В будет построение машины С.
3. Если мы теперь в качестве машины С выберем универсальный автомат, идентичный В, что в результате универсальный автомат В создаст копию самого себя. То есть его входом будет описание А, который строит В, а его выходом будет построение В.

Все это, конечно, зависит от того, может ли выходом автомата быть построение другого автомата, а это не теоретическая, а практическая трудность. Но можно представить себе, что в распоряжении универсального автомата имеется запас стандартных деталей, которые надо собрать в определенном порядке. В терминах машины Тьюринга можно сказать, что детали играют роль ленты.

Второй подход более абстрактен и содержит много упрощений. В частности, пространство берется двумерным и делится на клетки как шахматная доска, а время принимает дискретные значения. Машина занимает связное множество квадратов, и каждый квадрат может находиться в одном из некоторого числа допустимых состояний, включая состояние покоя (в том частном случае, который фон Нейман подробно исследовал, было 29 состояний). Задача состоит в том, чтобы найти такой набор правил перехода между состояниями и такой набор состояний в момент времени t = 0, чтобы машина воспроизводила сама себя, если состояние каждой клетки в данный момент зависит только от состояния ее и четырех ее ближайших соседей в предыдущий момент времени.

Такая постановка задачи привлекла и других ученых, включая Бёркса [19], Майхилла [20, 21] и самого Мура, работу которого мы только что упоминали.

Совершенно независимый подход к проблеме машинного самовоспроизведения, связанный с построением механических моделей, принадлежит Л. С. Пенроузу. Этот подход также привлек большое внимание, и Пенроуз описывал его много раз [22-26]. Он решил "придумать простые элементы или "кирпичи" с такими свойствами, чтобы из них можно было построить самовоспроизводящуюся машину" [25]. Для этого он сделал фанерные "кирпичи" такой формы, что когда их все погружали в коробку и эту коробку трясли, так что "кирпичи" приходили в контакт друг с другом, некоторые из них прочно скреплялись при этом между собой. Простой пример представляется моделью, в которой имеются два сорта "кирпичей", причем скрепляться могут только "кирпичи" разных сортов. И скрепляются они при этом только в том случае, если где-то в коробке уже есть хоть одна такая скрепленная пара. Тогда все происходящее можно рассматривать как самовоспроизведение уже скрепившейся "двухатомной молекулы", или "зародыша". Механическое объяснение такого поведения очень просто и быстро становится очевидным, когда видишь ее в действии, и при этом ее работа производит сильнейшее впечатление (см. рисунок на стр. 80).

Пенроуз заключает, что "самовоспроизводящиеся цепи из механических единиц, возможно, помогут объяснить, как на самом деле копируют себя нуклеиновые кислоты в живых клетках. Но более вероятно, что они помогут в понимании более простых систем, например тех, которые должны были предшествовать нуклеиновым кислотам в эволюции" [25].

Пенроуз, однако, не единственный, кто применяет механические модели для имитации самовоспроизведения. Джекобсон, например, построил модель в виде маленькой железной дороги, содержащую несколько элементов, способных собираться вместе [27], а Моровиц развил идею Джекобсона, построив более простую модель, содержащую электромагниты [28]. О работе Голдейкра и Бина мы в этой связи уже говорили.

Первое, что бросается в глаза при рассмотрении этих моделей, - это то, что они имеют удивительно малое отношение к развитию.

Если считать, что самовоспроизведение в этих моделях моделирует воспроизведение одним животным другого животного, то тот факт, что последнее обычно проходит стадию зародыша или оплодотворенного яйца, полностью игнорируется. Так, в моделях фон Неймана новая машина хотя и строится постепенно, шаг за шагом, а не создается готовой в один момент, все же этот рост управляется полностью извне той машиной, которая ее строит. То есть, одна машина строит другую машину, а не вторая машина строится сама на основе инструкций, данных ей первой машиной. Конечно, интересно, почему животные самовоспроизводятся не по способу фон Неймана, а развиваются автономно из чего-то на вид гораздо более простого, чем их родители (и неизбежно более маленького, так как семя само было частью родителя). Ответ, быть может, в том, что просто так легче. Вольперт (личное сообщение) заметил, что легче сделать бумажную птичку, пользуясь списком инструкций о том, как надо сгибать бумагу, чем рассматривая другую уже сделанную. Но, с другой стороны, скопировать картину легче, глядя на оригинал, чем с помощью списка словесных инструкций. Можно было бы предположить, что разница частично состоит в том, что в бумажной птичке части взаимосвязаны, как в животном, а в картине - в некотором смысле нет. Этим вопросом мы еще займемся в начале гл. 8.

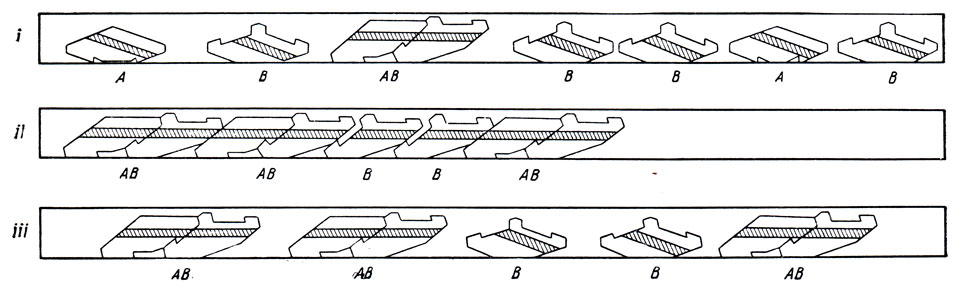
Все это связано с убеждением, высказанным в предыдущей главе, что развитие управляется изнутри. Конечно, для моделей Пенроуза не так очевидно, как для моделей фон Неймана, что образование новой машины управляется извне,- и соединятся два "кирпича" или нет, зависит частично от них самих,- но это зависит и от других "кирпичей", например от присутствия хотя бы одной готовой пары, как в описанной выше модели.

Возможен иной подход к самовоспроизведению: на уровне клеток, а не организмов. И, конечно, модели Пенроуза соответствуют не уровню организмов; сам Пенроуз, как мы видели, считает свои модели наиболее полезными в связи с уровнем еще более низким, чем клеточный,- с молекулярным уровнем. (Фон Нейман, конечно, не занимался моделированием какого-либо определенного уровня: его интересовала в первую очередь абстрактная проблема самовоспроизведения автоматов.)

Повторим, однако, что проблема развития совершенно отлична от проблемы самовоспроизведения, потому что проблема развития основывается на проблеме самовоспроизведения. Она предполагает, что элементы могут воспроизводить себя, и, как мы видели в предыдущей главе, спрашивает: если это так, то как в системе, составленной из таких самовоспроизводящихся элементов, может возникнуть порядок? То есть каковы принципы, управляющие функциональной и (особенно) пространственной дифференцировкой системы, развивающейся путем непрерывного самовоспроизведения составляющих ее элементов? Следовательно, вопрос о том, как одна клетка, содержащая ядро, цитоплазму и оболочку, может воспроизвести себя, совершенно отличен от проблемы биологического развития, и точно так же вопрос о том, как автомат может воспроизвести себя, отличен от вопроса о том, как система, составленная из таких автоматов, может дифференцироваться.

Конечно, нет никаких причин, чтобы не пытаться выразить инструкции, определяющие развитие, на языке более низкого уровня, и всякая теория развития всегда должна находиться в согласии с известными данными об этом нижнем уровне. Несомненно, все, что мы узнаем о принципах развития, раньше или позже должно соединиться с данными о том, как воспроизводятся клетки, и вполне естественно спрашивать, как записать решение этой проблемы в терминах, скажем, кода ДНК (и в гл. 7 мы, следуя этим соображениям, предпримем попытку выразить некоторые представления о развитии в генетических терминах.) Возможно и обратное,- что знание о том, как работают гены, наметит возможные пути применения принципов развития к реальным живым организмам. Но на теперешнем раннем этапе учет этих данных скорее приведет к ненужным сложностям при попытках понять развитие как таковое.

Этот раздел хорошо можно подытожить высказыванием Бёркса и Вана Хао:

Модели фон Неймана можно строить как на уровне клеток, 
так и на уровне целых организмов, но в обоих случаях они, 
по-видимому, лишь частично решают задачу. Процесс деления 
клеток - это только составная часть всего процесса ... 
а воспроизведение совершенно готовых систем исключает 
важный процесс развития от детства до зрелости [29].