Основные модели

Начнем с самых простых программ и попытаемся постепенно увеличивать их сложность. В конце концов, прежде всего мы должны показать, что самовоспроизведение машинных программ вообще возможно, что a priori никоим образом не очевидно, и должно представлять интерес для тех, кто занимается самой проблемой самовоспроизведения.

Самая простая программа занимает всего одну ячейку и выглядит следующим образом:

Работа программы начинается с ячейки 192.

В этой программе имеет место полное самообращение, поскольку обе команды, из которых она состоит, воспроизводятся. К сожалению, воспроизведение повторяется всего два раза, после чего в накопителе все время остается 02 192:20 194. "Проверочная программа 803 С 2" дает возможность обследовать любую часть памяти машины: она печатает ее содержимое в виде команд. С помощью этой программы, которую мы будем использовать для всех остальных моделей, мы видим, что содержимое памяти по окончании работы программы таково:

Эта модель позволяет заключить, что программа, занимающая только одну ячейку в этой машине, не может осуществить более длинный ряд последовательных самовоспроизведений. Но с использованием двух ячеек можно написать такую программу, правда, заполнив при этом заранее и накопитель:

Перед началом работы программы надо записать в накопитель 22 192/20 193. Программа начинает работать с ячейки 193.

В этом случае проверочная подпрограмма выдает нам:

Этот продолжающийся процесс самовоспроизведений не обрывается сам, и работу программы приходится останавливать вручную с пульта управления. Таким образом, число воспроизведений целиком зависит от того, когда происходит остановка. Это число записано в ячейке 192, служащей счетчиком.

Недостаток этого способа моделирования развития в том, что он не поддается обобщению, поскольку объем накопителя равен объему лишь одной ячейки, а только его содержимое и воспроизводится; эта модель включена, следовательно, скорее для полноты и ничего не дает. Однако следующая модель, хотя она тоже очень коротка и проста, важнее, чем две описанные, потому что ока представляет нам более широко применимый способ развития. В этой модели программа поделена на две части, и в том ее конкретном варианте, который приведен ниже, используется переадресация, хотя это и не существенно и без нее вполне можно было бы обойтись. Здесь одна часть, та, которая воспроизводится, использует другую, чтобы совершить воспроизведение. Иными словами, то слово, которое воспроизводится, в действительности само себя воспроизводит, но делает это путем передачи управления "подпрограмме воспроизведения". (Аналогично используется выход R в автоматах, описываемых в следующей главе.) Управление по-прежнему происходит изнутри, что самое главное, хотя сам акт воспроизведения теперь осуществляется извне. Программа этой модели такова:

Третья модель

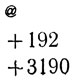
Работа программы начинается с ячейки 192.

(Во второй команде ячейки 3191 на месте операции поставлено 20 затем, чтобы при каждом обращении к ней после прибавления вследствие В-модификации содержимого ячейки 3190 получалось 40.)

В этой модели, как и в предыдущих, рост происходит в арифметической прогрессии и сам себя не обрывает. Однако в данном конкретном случае рост обрывается благодаря положению "подпрограммы воспроизведения": поскольку она помещена в ячейках 3190 и 3191, то рост обрывается, дойдя до этих ячеек, и программа останавливается, поскольку прежнее их содержимое стирается. Такое использование части программы как "буфера", конечно, необычно, и если бы нужно было остановить работу машины каким-нибудь другим способом, то было бы безопаснее поместить эту подпрограмму перед остальной частью программы, а не после нее, как мы это сделали.

Если напечатать результат роста с помощью проверочной программы, то станет видно, что во всех ячейках, от 192 до 3189, записано слово 22 3190:40 3190.

Следующая модель тоже растет арифметически, но отличается от предыдущей во многих отношениях:

1. Программа состоит из одного блока, т. е. нет отдельных подпрограмм. Управляющие команды расположены перед той командой, которая воспроизводится. Снова используется В-разряд.
2. Рост этой модели в отличие от предыдущих ограничен, т. е. это самоограничивающая модель. (Мы уже говорили в гл. 2, что первый вопрос, возникающий в связи с каждой развивающейся системой,- это как она может ограничить свое развитие, остановив его.) Это делается обычным способом, с помощью счетчика, вставленного в цикл, считающего число воспроизведений и в нужный момент останавливающего программу. Правда, нужно заметить,что хотя программа в целом сама себя останавливает, но та ее часть, которая определяет число воспроизведений, сама не воспроизводится. В следующих моделях этот недостаток, конечно, надо будет устранить. Заметим, однако, что в известной степени то, что мы моделируем,- это самовоспроизведение ядер, происходящее в недифференцированной массе цитоплазмы, действительно часто имеющее место на раннем этапе развития эмбриона. И не исключено, что цитоплазма оказывает существенное влияние на ход этого самовоспроизведения.
3. Каждая новая клетка воспроизводит себя, т. е. делает копию себя самой, а не копию исходной клетки. Таким образом, не воспроизводится снова и снова первая команда, а каждая новая команда воспроизводит себя в следующей ячейке. Это удается сделать, используя отдельную команду, работающую каждый раз с новой, а именно последней заполненной ячейкой, для чего используется В-разряд.
4. Наконец, этот процесс является скорее процессом развития, чем просто роста или накопления, поскольку теперь каждая выросшая клетка отличается от других. (Под "клеткой" мы всюду в этой главе будем понимать ту часть программы, которая воспроизводится.) Причина этого не просто в том, что каждая новая клетка воспроизводит себя, так как в этом случае конечный результат, выданный проверочной программой, совпадал бы с результатом, полученным в предыдущих моделях, где каждая новая клетка была копией исходной клетки. Тогда в обоих этих случаях получился бы ряд одинаковых клеток. Здесь же вторая половина воспроизводимого слова не участвует в работе программы и может использоваться для нумерации. К ней и прибавляется единица при каждом новом воспроизведении (с помощью операции 02), в результате чего с помощью проверочной программы мы обнаруживаем, что все слова различны. Это различие было бы, конечно, поверхностным, если бы не то обстоятельство, что его можно легко превратить в "настоящее" или функциональное различие. Для этого достаточно, чтобы этот счетчик обеспечивал передачу управления от всех слов к разным подпрограммам, представляющим различные функциональные свойства, которые могут как-то менять клетки, которые передали им управление, или даже, может быть, ход развития в целом. Каждую такую подпрограмму можно рассматривать как эквивалент гена, и это напоминает нам о проведенной в предыдущей главе аналогии между яйцом и программой для вычислительной машины, когда мы предположили, что все гены (или хотя бы некоторые из них) могут действовать наподобие подпрограммы. Первые ячейки всех этих подпрограмм должны, конечно, идти подряд друг за другом, так как их адреса отличаются на единицу, но в них можно поместить команды передачи управления, отсылающие к разным местам в памяти машины, где уже поместить основные части этих подпрограмм; формально можно сказать, что эти команды передачи управления соответствуют генам в каждой клетке. Подпрограммы при этом могут быть любой длины.

С другой стороны, если бы удалось устроить передачи управления между этими клетками, то в каком-то смысле возникла бы пространственная или топологическая структура, причем передачи управления соответствовали бы каналам связи.

Вот сама программа:

Четвертая модель

Работа начинается с ячейки 200.

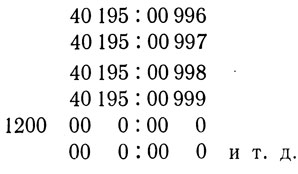
Программа останавливается, заполнив 999 ячеек, так что, включая клетку в исходной программе, построенный "организм" содержит 1000 клеток. Вот содержимое нескольких последних ячеек по окончании развития: 40 195:00 996 40 195:00 997

При развитии реальных организмов часто сначала происходит рост массы, а уже потом дифференцировка. Пятая модель - это то же самое, что четвертая, с той разницей, что она состоит из двух блоков: первый блок делает то же, что четвертая программа, только без дифференцировки, а второй блок осуществляет дифференцировку, причем вступает в работу лишь тогда, когда первый блок кончает работать. Заметим, что точно так же, как и в четвертой модели, нарощенные ячейки могут передавать управление другим частям программы.

При построении этой программы надо было позаботиться о том, чтобы первый блок, работая и заполняя ячейки, не испортил второй блок; в данном случае, когда второй блок начинается с ячейки 3190, это обеспечивается тем, что число клеток в построенном организме равно 1000. Однако положение было бы труднее, если бы в программу входили другие блоки, осуществляющие функциональную дифференцировку, и поэтому, возможно, вообще было бы лучше поместить оба блока рядом в самом начале, а новые клетки помещать уже после них.

Пятая модель задается следующей программой:

Пятая модель

Работа начинается с ячейки 195, т. е. 3,1.

Результат работы этой программы точно такой же, что для четвертой модели: 999 новых ячеек заполняются словами вида "40 195 : 00 N" (где N пробегает все значения от 1 до 999), и в результате система содержит 1000 ячеек, различающихся числом N.