Дальнейшие усложнения

Пока мы построили что-то вроде искусственной, машинной тканевой культуры, причем крайне примитивной; при этом, как в идеализированной культуре ткани, управление ростом и дифференцировкой было пока внешним по отношению к клетке (кроме случая нежелательного прекращения роста в первой модели). Однако, согласно аксиомам, принятым в гл. 2, развитие должно управляться изнутри, и мы должны, следовательно, искать способ заключить все команды, управляющие размером и дифференцировкой в системе внутрь клетки, т. е. той части программы, которая воспроизводит себя. До сих пор размер клетки был ограничен одной ячейкой, содержащей немногим больше чем одну команду передачи управления, и теперь, следовательно, его надо увеличить. Если мы сумеем найти метод, подобный примененному выше, которым клетка могла бы использовать остальную часть программы, чтобы воспроизвести себя целиком, как бы велика она ни была, то с помощью этого метода мы сможем строить более сложные и реалистичные модели развития, применимые к клеткам любого размера и сложности. Требуется, очевидно, что-то вроде универсальной подпрограммы роста, которая даст любой "подпрограмме семени", помещенной в машину, возможность самовоспроизводиться с ее помощью и, следовательно, расти и проявлять свои возможности развития. В результате "программа семени" сможет расти и в ходе этого роста автономно дифференцироваться любым способом, каким она пожелает.

Вот пример такой подпрограммы роста:

Программа роста 1

Работа начинается с ячейки 195.

Эта подпрограмма придает всякой подходящей "программе семени" способность самовоспроизведения. Требования к "программе семени" следующие:

1. Она должна начинаться с ячейки 203, и в этой ячейке должно быть записано число всех ячеек в клетке.
2. В клетке должна в некотором месте стоять команда передачи управления ячейке 197 программы роста.

Никаких других ограничений на программу семени нет.

Поэтому простейшая программа семени содержит только названные ячейки и выглядит так:

Программа семени 1

Эта программа в соединении с программой роста 1 приводит к неограниченному росту в арифметической прогрессии, и модель в целом в некоторых отношениях похожа на третью модель, тоже в действительности состоящую из подпрограммы роста и подпрограммы семени. Из-за этой неограниченности роста процесс приходится останавливать вручную с пульта управления. Проверочная программа, конечно, выдает непрерывный ряд одинаковых двухкомандных клеток.

Следующий шаг, очевидно, должен состоять в придании семени способности ограничить рост. Но это требует еще одной ячейки в семени, свободной от команд, в которой должно быть записано, сколько раз семя надо воспроизвести, и которую можно использовать как счетчик. Теперь семя будет начинаться с двух ячеек, не занятых командами, и во второй из них должно храниться число воспроизведений, которое удобно записать со знаком минус. Поскольку есть опасность принять это число за пару команд, то лучше, чтобы программа роста передавала управление прямо третьей ячейке каждой клетки, а не первой. Это достигается небольшим изменением в ячейке 202 программы роста 1; для ясности выпишем полностью полученную программу и присвоим ей номер 2:

Программа роста 2

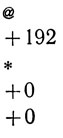
Требования к "программе семени", предъявляемые этой программой, конечно, точно такие же, что и в случае программы роста 1, и работа всей программы по-прежнему начинается с ячейки 195. Тогда простейшая самоостанавливающаяся "программа семени" записывается так:

Программа семени 2

Число во второй ячейке этой программы, конечно, ограничено лишь величиной памяти машины, причем надо помнить, что часть памяти уже занята проверочной программой С2. Результат работы той конкретной программы, которая приведена выше, состоит в том, что клетка воспроизводится 100 раз без изменений, так что заполняются 500 новых ячеек.

Эта программа семени в ее теперешнем виде не предусматривает, однако, обращения ни к одной из построенных клеток, а только к исходной, к семени. То есть когда любая клетка обращается к счетчику определяющему, сколько надо выполнить воспроизведений," она обращается не к той ячейке, которая находится в ней, а к той, которая принадлежит первой клетке, т. е. к постоянной ячейке с адресом 204. Подобно этому останов обеспечивает постоянная ячейка 207, а не последняя ячейка последней клетки. Если говорить о счетчике числа воспроизведений, то вполне допустимо, чтобы, если в реальном организме было что-то вроде такого счетчика, этим занималась бы и объединяла бы деятельность всего организма какая-то одна клетка или одна группа клеток. Но, может быть, предпочтительнее было бы, если бы каждая клетка могла обращаться к своим собственным ячейке-счетчику и ячейке остановки. При этом счетчик мог бы служить для предварительной разметки для дифференцировки. Но гораздо важнее то, что, если мы хотим запрограммировать клетку, состоящую из многих взаимодействующих частей,- а это вполне естественное для нас желание - то эти части клетки должны быть способными адресоваться именно друг к другу внутри одной и той же клетки, а не к соответствующим частям исходной клетки. В противном случае разные клетки системы не смогут выполнять разные функции. Во всяком случае, раз мы хотим построить общую программу роста, применимую к любому семени, эта программа обязана предусматривать и такую возможность. (Кроме того, не следует забывать, что каждая клетка должна сохранять и некоторую способность внешнего обращения; как минимум все клетки должны иметь возможность передать управление какой-то специальной ячейке в программе роста).

Простейший способ сделать передачу управления внутри клетки возможной - это сделать так, чтобы при каждом воспроизведении к N-части каждой команды прибавлялось число ячеек в клетке. Этого можно достичь, изменив программу роста так, что она станет в сущности "программой роста и изменения адресов". Для этого достаточно просто добавить к программе команду 199, как показано ниже, после чего придется сделать еще несколько мелких изменений. В результате получаем новую программу:

Программа роста 3

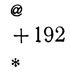
Программа начинает работать с ячейки 195.

Семя теперь должно начинаться с ячейки 204, так как эта программа роста на одну ячейку длиннее, чем две предыдущие. Как и прежде, в первой ячейке семени должно быть записано число ячеек в клетке, подлежащей воспроизведению; кроме того, как и прежде, семя должно содержать в подходящем месте команду передачи управления в ячейку 197 программы роста.

По причинам, которые станут ясны после знакомства с программой семени, приводимой ниже (программа семени 3), первые команды ячеек 196 и 197 теперь работают с содержимым ячейки 192, а не первой ячейки семени. Поскольку в ячейке 192 записывается точно то же самое, результат не меняется. Однако теперь, после выполнения команд ячейки 195 (что происходит только один раз - в самом начале работы), программа роста и программа семени 3 абсолютно автономны и работают каждая только со своими ячейками, если не считать передачи управления между ними и существенного обращения к 192 третьей ячейкой семени.

Итак рассмотрим теперь программу семени 3, простейшую самоограничивающуюся и самообращающуся программу семени из всех, к которым применима программа роста 3:

Программа семени 3

В результате работы всей программы эта клетка из 9 ячеек воспроизводится пять раз, так что получившийся "организм" содержит шесть таких клеток и заканчивается ячейкой 257. Все клетки различаются числами, стоящими в их вторых ячейках.

Работа программы, возможно, требует некоторых пояснений:

1. Поскольку адреса команд модифицируются с помощью операции 04 в ячейке 199 программы роста так, чтобы каждая клетка была автономна, как оно и есть на самом деле, то все эти команды должны занимать только вторую половину ячеек: ведь операция 04 прибавляет число ячеек в клетке только ко вторым половинам воспроизводящихся ячеек. Этим объясняется большое количество пустых мест в первых половинах ячеек в программе семени. Конечно, эта программа тем самым занимает больше места.
2. Однако некоторые команды, например команда передачи управления программе роста, наоборот, не должны меняться. Их, очевидно, надо поместить в первые половины ячеек, что и сделано в отношении третьей и восьмой ячеек программы семени. Эти ячейки при работе 199 не могут измениться, если только число ячеек в семени не окажется таким огромным, что его прибавление затронет первую половину ячейки^*, но пока это вряд ли возможно, во всяком случае, на машине 803. Итак, команды, помещенные в первых половинах ячеек, работают с постоянными ячейками.
3. К сожалению, поскольку счетчик - это число, мы не можем выбирать, в какую половину ячейки его поместить, оно всегда будет находиться во второй. (Фактически его часто будет удобно брать отрицательным, и тогда оно будет заполнять собой всю ячейку). Следовательно, неизбежно всякий счетчик, в какой бы ячейке он ни находился, будет изменяться при каждом воспроизведении, что гибельно для программы. Простейший способ справиться с этой проблемой - это сделать так, чтобы каждая клетка сама исправляла свой счетчик, вычитая из него то самое число ячеек в клетке, которое программа роста прибавила. Это должно быть сделано, очевидно, до того, как сработает хотя бы одна команда в клетке. Все детали того, как это сделать, можно понять, рассмотрев данную выше программу семени.

^* (Или командную часть второй половины.- Прим. перев.)

Далее необходимо отметить, что программа семени почти любой сложности сможет расти лишь при условии, что она удовлетворяет нескольким простым требованиям: начинается с ячейки 204, в которой записано число занимаемых ею ячеек, и в какой-то момент передает управление ячейке 197. Кроме того, конечно, передача управления от программы роста к клетке должна быть изменена так, чтобы перескочить через счетчики и адресоваться сразу к ячейкам, занятым командами. Этого удалось достичь, вписав число ячеек, через которые надо перескочить в адресную часть второй половины ячейки 203 программы роста (см. программу роста 3). Можно было поступить иначе: поместить все счетчики, константы и другие ячейки, не занятые командами, вместе в конце программы в виде "хвоста" (по выражению фон Неймана [5]), а в адресной части второй команды 203 записать 1. Очень может быть, что, вообще говоря, так было бы удобнее, потому что тогда на программу роста вообще можно было бы не обращать внимания и применять ее к одной программе семени за другой, не меняя ее каждый раз. К тому же различные, но мало отличающиеся друг от друга варианты программы семени можно было бы запускать в машину, не меняя основную часть программы семени (только следить за первой ячейкой, в которой пишется общее число ячеек семени), а меняя лишь хвост программы. Во всяком случае, если бы все некомандные ячейки программы были собраны в конце, легче было бы уследить, чтобы программа не приняла их за команды.

Итак, теперь уже можно поставить вопрос о том, как использовать рассмотренный здесь тип моделей, чтобы промоделировать на машине процесс, близкий к реальному развитию организмов. Самое трудное здесь - решить, как представить организм на языке машины. Выберем какой-нибудь конкретный вид и попытаемся промоделировать хотя бы начальный этап его развития. Поскольку более всего биологам знаком морской еж и его раннее эмбриональное развитие хорошо иллюстрирует свойства, присущие многим видам, выберем его как пример.

После оплодотворения яйцо морского ежа начинает интенсивно дробиться и в результате превращается в полый шар, бластулу, состоящую из большого числа клеток, бластомеров. Некоторые из них, первичные клетки мезенхимы, продвигаются во внутренность сферы, или бластоцель, и двигаются по внутренней стенке бластулы, пока не занимают на ней определенных положений, прикрепившись к отдельным клеткам. (После этого наступает гаструляция, которую мы в этом кратком примере не будем описывать.) Из сказанного видно, что первый этап состоит из трех существенных частей:

1. Непрерывное дробление, приводящее к образованию бластулы.
2. Самоузнавание и выселение из бластулы первичных клеток мезенхимы.
3. Прикрепление этих клеток к специальным клеткам бластулы. Их расположение, видимо, определяется клетками бластулы, которые служат на самом деле "матрицей"; первичные клетки мезенхимы к ней прикреплены.

Основная программа, следовательно, должна состоять из трех частей:

1. Программа воспроизводит себя определенное число раз подобно самоостанавливающимся программам семени, описанным выше. Теперь, однако, последняя клетка, вместо того чтобы остановить работу, передает управление назад, второй части начальной клетки. В некотором смысле, следовательно, образуется круг, который можно рассматривать как аналог сферы бластулы, точно так же как рост в арифметической прогрессии заменяет у нас для удобства рост в геометрической прогрессии. Однако надо признать, что этот круг образуется не так, как бластула, поскольку он возникает как таковой в топологическом смысле лишь на последнем шаге.
2. В ходе воспроизведений все клетки нумеруются. Затем каждая клетка сравнивает свой номер со списком номеров клеток, которым суждено стать "первичными клетками мезенхимы". Такой список имеется готовым в конце каждой клетки. Если номер клетки совпадает с одним из номеров из этого списка, то клетка передает управление своей третьей части, если же нет, то она передает управление второй части следующей клетки.
3. Каждый раз, когда управление передается третьей части какой-нибудь клетки, происходит следующее: эта клетка просматривает номера всех клеток подряд, пока не находит клетку с номером, совпадающим с одним из номеров второго списка, также приданного всем клеткам. Затем она проверяет, не прикрепилась ли к этой клетке уже другая; для этого в каждой клетке припасена специальная ячейка, вначале пустая, в которую вписывается-1, если к этой клетке прикрепляется другая клетка. Если наша клетка находит такую клетку, к которой еще ничего не прикрепилось, она записывает у себя в определенном месте номер, присвоенный ей при воспроизведении, и вычитает 1 из содержимого упомянутой ячейки этой клетки. В противном случае она продолжает проверку других клеток. Найдя такую клетку и выполнив все описанные действия, она передает управление второй части следующей клетки; если же она так и не находит клетки, к которой может прикрепиться, то она останавливает работу программы.

Кроме этих трех основных частей, программа должна содержать еще две части. Одна из них - это блок восстановления, вроде того, который применен в программе семени 3; он восстанавливает счетчики, разметку клеток и команды абсолютной передачи управления после того, как их портит программа роста во время воспроизведения. Имеется еще следующая трудность: как сможет клетка передавать управление в заданное место, например в начало второй части другой клетки, если длина всех клеток зависит от длины их хвостов? Для ее преодоления надо ввести поправочные команды, меняющие адреса этих команд передачи управления в зависимости от длины хвоста.

И наконец, еще одна часть программы- это, конечно, сам хвост, содержащий списки адресов, хотя, пожалуй, правильнее было бы считать его главной частью программы, а то, что здесь названо основной частью программы, считать подпрограммой, поскольку она, оставаясь постоянной, все время получает управление из разных мест. Как бы то ни было, хвост определяет, как конкретно будет преобразовываться программа - сколько клеток должно получиться, какие из них станут первичными клетками мезенхимы и т. д.,- а также содержит много других ячеек, не содержащих команды и нужных для разных частей программы. Особенно важно, чтобы все эти данные были в конце, поскольку длина хвоста меняется в зависимости от числа первичных мезенхимных клеток и от числа клеток, к которым они могут прикрепляться, и если списки их будут не в конце, то при каждом изменении в списках придется всю программу переписывать (если только вся программа не будет написана в относительных адресах). В общем в состав хвоста должны входить: счетчики, которыми будут пользоваться первые, вторые и третьи части соответственно; счетчик подпрограммы восстановления; записанное с обратным знаком число будущих воспроизведений; число первичных мезенхимных клеток и число ячеек, которые занимает хвост; номер, присваиваемый клетке при воспроизведении, т. е. ее положение в ряду клеток; пустая ячейка для записи -1, если к этой клетке прикрепится другая, и еще одна ячейка, чтобы записать номер той клетки, к которой она прикрепилась, если это первичная мезенхимная клетка; наконец, список номеров первичных мезенхимных клеток и список номеров клеток, к которым они могут прикрепляться (той же длины). Первая ячейка клетки, ячейка 204, в которой стоит число ячеек в клетке, включая хвост и все другие ее части, функционально тоже входит в состав хвоста, хотя и расположена отдельно от него.

Теперь уже виден целый ряд недостатков использования машинных программ в качестве моделей, хотя до сих пор о них явно не говорилось.

Во-первых, на ранней стадии исследования такой сложной проблемы, как эта, модели, которые нужны,- это поисковые модели, главное назначение которых помочь хотя бы частично понять основные принципы. Однако теперь должно быть уже ясно, что машинные модели неособенно пригодны для этой цели и что машины полезны на самом деле скорее для проверки гипотез, чем для их выдвижения. Следовательно, машинные модели, по-видимому, менее полезны на ранней стадии разработки теоретической проблемы, чем на более поздних стадиях.

Это не означает, что программирование может обойтись без формулирования каких-то идей даже на раннем этапе исследований; но эти идеи, возможно, окажутся бесполезными или непригодными в применении к той реальной ситуации, которая моделировалась. Например, из того факта, что развитие на машине требует наличия счетчиков для своего управления, не обязательно следует, что счетчики в том или ином виде присутствуют в реальных клетках: там управление может осуществляться совсем другими способами (хотя всякий такой способ обязательно содержит функциональный эквивалент счетчика). Сходным образом, когда программы имеют вид низкоуровневых моделей, аналогия между ними и объектом моделирования может быть несколько произвольной, что ясно видно на примере только что описанной довольно жесткой и искусственной модели морского ежа. Такая программа, следовательно, может воплощать лишь поверхностные черты моделируемого процесса, хотя это, конечно, необязательно. Все это не следует воспринимать в том смысле, что машинный подход не может повлечь за собой интересных теоретических выводов и один такой вывод в отношении развития, сделанный на основе описанных выше моделей, обсуждается в гл. 8 в связи с самообращением при развитии.

Верно также и то, что в программировании средства иногда становятся целями и задачи программирования могут заслонить первоначальную проблему. Отчасти это объясняется тем, что программы обычно настолько чувствительны, что малейшая ошибка, даже описка, может помешать работе всей программы и вызвать потерю времени. Но главная причина - это то, что вычислительные машины в принципе неудобны для представления многих процессов. Хорошим примером из области развития может служить трудность программирования пространственной дифференцировки; по этой причине формирование структуры в моделях, описанных выше, определялось скорее функциональной, чем пространственной дифференцировкой. В настоящее время представление пространственных систем более чем одного измерения на машинах всегда несколько произвольно^*, потому что память машин линейна, и возникает общая проблема моделирования параллельных систем одномерными. Быть может, это одна из наиболее серьезных причин, ограничивающих возможности современных вычислительных машин, и поэтому вопрос о проектировании и создании машин с нелинейной памятью, который как раз теперь разрабатывается [7, 8], представляет огромный интерес.

^* (Эти замечания автора не совсем понятны, ибо программирование любой сколько-нибудь сложной задачи на ЭВМ достаточно трудоемко и, разумеется, неоднозначно, и в этом смысле произвольно.- Прим. ред.)

При попытках моделирования пространственной дифференцировки на машине возникает и другая трудность, связанная с предыдущей: если система должна расти не только на конце, как описанные выше модели, то, очевидно, части системы должны раздвигаться, чтобы дать место новым частям. Идеальным способом преодоления этой трудности было бы построить "обобщенную" универсальную вычислительную машину вроде той, что предлагают Бёркс и Ван Хао [9], в которой между любыми двумя ячейками может возникнуть новая ячейка.

В данный момент, однако, можно было бы применить способ, предложенный в этой главе и реализованный в модели развития морского ежа; по этому способу можно реализовать на машине пространственную или топологическую дифференцировку, если пронумеровать все клетки, и затем использовать этот номер при работе других клеток, которые тем самым можно будет считать взаимодействующими с этой и которые могут фактически с пей взаимодействовать в смысле взаимной передачи управления. Так, чтобы построить из пяти клеток Y-образную фигуру, их надо соединить так:

Возможно, этот способ неуклюж, но он позволяет моделировать пространственные системы. Надо только следить при моделировании развития таких систем, чтобы программа не приняла параллельные (т. е. одновременные) события за последовательные. Например, если одно из двух таких событий машина выполняет раньше, то его результаты не должны влиять на второе, которое мыслится происходящим одновременно с первым. Этого не всегда легко добиться, и в следующей главе мы опишем модель, с которой можно работать просто с помощью карандаша и бумаги, и она в этом отношении проще, так как там одновременные события действительно происходят "одновременно". Модель, описываемая в следующей главе, возможно, больше подходит на данном этапе еще и потому, что использует идеализированные вычислительные машины типа машины Тьюринга, и в этом смысле она принципиально проще, чем модели, программируемые на реальных машинах, вследствие чего она скорее может помочь на пути к пониманию процесса развития.

Подведем итог того, что проделано в этой главе. В ней показано, что на машинах можно программировать нетривиальные модели развития, и предложен метод, с помощью которого любую идею, относящуюся к развитию, можно в принципе реализовать на машине^*. Надо надеяться, что машина может быть особенно полезна на более позднем этапе изучения, когда потребуются способы как проверки, так и демонстрации общих принципов развития.

^* (С этими утверждениями нельзя согласиться. Рассмотренные модели очень просты, их программирование, безусловно, не составляет труда. Неясно также, что автор имеет в виду, говоря, что "предложен метод, с помощью которого любую идею, относящуюся к развитию, можно в принципе реализовать на машине". Дело в том, что в принципе любую математическую модель, если только хватит для этого времени, можно запрограммировать на машине.- Прим. ред.)