Глава 7. Управление пространственной структурой

Модель управления пространственной структурой

Регенерацию, во всяком случае регенерацию у простых организмов, где она может быть полной, можно считать одной из форм развития, поскольку конечным состоянием обоих процессов является организм, обладающий полным комплектом органов и тканей. Однако можно пойти дальше: одной из самых ярких особенностей живого мира является то, что размеры частей организма определяются размерами целого. Следовательно, в процессе развития части, поскольку речь идет об их размерах, растут согласованно друг с другом. Подобно этому, при полной регенерации величина регенерировавшей части определяется величиной всего организма. Тогда, очевидно, должен существовать какой-то способ регуляции относительными размерами частей организма как в процессе роста (эмбриональное развитие), так и в зрелом состоянии (регенерация), и природа этой регуляции остается основной проблемой развития. Эта проблема важна не только сама по себе; изучение развития с этой точки зрения может привести к лучшему пониманию проблемы образования пространственной структуры.

Далее, если происходит вмешательство в ход развития извне, оно часто само исправляет ошибку. Если вызвать какое-либо нарушение в области эмбриона, т. е. часть клеток убрать, или добавить новые, или перемешать клетки, то очень часто после этого развитие протекает нормально. Например, как показал Дриш [1], половина эмбриона морского ежа, если она отделена на достаточно ранней стадии развития, развивается в личинку, имеющую нормальные пропорции, хотя и меньший, чем обычно, размер. В подобном случае говорят, что имела место "регуляция", и мы можем рассматривать ее скорее как форму регенерации или исправления ошибки, включенную в процесс развития, чем как регенерацию или исправление ошибки в зрелом организме. Способность к регуляции, по-видимому, - широко распространенное свойство ранних этапов развития животных, и во всяком случае, чем раньше в ходе развития происходит повреждение, тем больше вероятность, что оно будет полностью исправлено. (У некоторых видов, которые мы имели в виду, говоря о "мозаичных яйцах", способность к регуляции практически исчезает при оплодотворении.)

Поскольку генотип всех клеток предполагается одинаковым, соотношение пропорций частей при нормальном развитии, регуляции и регенерации должно быть надклеточным в смысле существования некоторого "целого", независимого от конкретных частей, составляющих его. Оно должно в то же время в конечном счете определяться набором инструкций, данных индивидуальной клетке. Как всегда при изучении развития, вопрос о том, как такой способ управления может возникнуть из совокупности одинаковых наборов инструкций, является загадочным. Существует мутантная форма слизистого гриба Dictyostelium discoideum, способная образовывать нормальные плоды, состоящие из спор, клеток ножки и базальных клеток, приблизительно в одних и тех же пропорциях, несмотря на то, содержат ли они сотни тысяч клеток или всего десять клеток. (См. фотографии в [2].) Как может подобная организация сохраняться в таком большом диапазоне размеров? Если вырезать половину почки конечности или перемешать две такие почки, образуется одна пропорциональная почка. Ясно, что в таких случаях управление пространственной структурой не зависит от какой-либо конкретной клетки, но включает в себя все клетки независимо от того, где в ткани находятся те или иные конкретные клетки этой ткани. Таким же свойством обладает и гидра, поскольку ее можно разрезать на маленькие кусочки, а потом их соединить в случайном порядке, и они реорганизуются заново в полноценный организм [3]. Как объяснить эти явления, не прибегая к витализму ни в какой его форме?

Попробуем прежде всего сформулировать проблему управления пространственной структурой, будь то развитие, регуляция или регенерация, в виде простой общей модельной ситуации. Вот один из возможных способов постановки проблемы.

Как в организме (или в ткани), состоящем из клеток с идентичными наборами инструкций, сохраняется определенное пространственное расположение функционально различных клеток, независимое от размеров организма (или массы ткани) и независимое от наличия или отсутствия каких-либо определенных клеток и их взаимного расположения? (Решение этой проблемы будет означать и решение вопроса о том, как такое расположение возникает вначале.)

Чтобы исследовать эту проблему в принципе, мы будем говорить о некоторой абстрактной ткани и сделаем следующие упрощения:

1. Ткань одномерна, т. е. представляет собой прямолинейную цепочку из N клеток.
2. В то время как генотип всех клеток одинаков, фенотип может принимать одну из двух различных форм, т. е. каждая клетка находится либо в состоянии X, либо в состоянии Y.

Проблема в ее простейшем варианте теперь формулируется так: как может такая система организоваться так, чтобы:

1. половина клеток всегда была в состоянии X, а половина - в состоянии Y;
2. эти два множества клеток были пространственно разделены друг от друга, так чтобы первая половина цепочки состояла из клеток X, а вторая половина - из клеток Y;
3. как сделать так, чтобы это положение восстанавливалось при прибавлении, удалении и перестановке этих одинаковых клеток?

Как и в предыдущих главах, давайте посмотрим, не удастся ли решить эту задачу, задав тот набор инструкций, который будет содержать каждая клетка. Модель, удовлетворяющая всем приведенным здесь условиям, получается, если каждая клетка имеет такой набор инструкций:

1. Если слева от тебя нет клеток, то пометь себя числом +1 и передай это число соседней клетке справа.
2. Если справа от тебя нет клеток, то пометь себя числом -1 и передай это число соседней клетке слева.
3. Если ты получила от соседней клетки положительное число, то прибавь к нему 1, пометь себя получившимся числом и передай его соседней клетке с другой стороны.
4. Если ты получила от соседней клетки отрицательное число, то вычти из него 1, пометь себя получившимся числом и передай его соседней клетке с другой стороны.
5. Если ты пометила себя двумя числами, то сложи их.
6. Если результат этого сложения положителен, то приди в состояние X, а если он отрицателен, то приди в состояние Y.

Следующая диаграмма наглядно показывает работу этой системы на примере цепочки из девяти клеток:

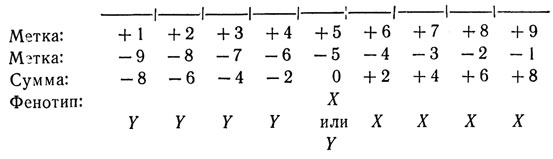
Возможности этой модели, конечно, ограничены тем, что она может управлять расположением клеток только двух типов. Допустим, что мы хотим обобщить эту модель так, чтобы цепочка клеток делилась не только на два, но и на три, четыре, вообще N равных кусков.

Это можно сделать следующим образом: клетки теперь не складывают свои метки, а составляют из них дробь, и каждая клетка определяет свой фенотип в зависимости от величины этой дроби.

Например, пусть мы хотим, чтобы система разделилась на три равные части, независимо от ее общей длины, так же, как раньше мы хотели, чтобы она разделилась на две равные части. Диаграмма, приводимая ниже, показывает, как это можно сделать:

Теперь напишем правила, по которым клетки определяют свой фенотип:

Если отношение меньше чем 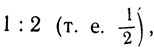то клетка переходит в состояние X.

Если отношение больше чем 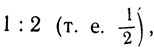но меньше чем 2:1 (т. е. 2), то клетка переходит в состояние Y.

Если отношение больше чем 2:1 (т. е. 2), то клетка переходит в состояние Z.

Следуя этим правилам, клетки образуют следующую картину:

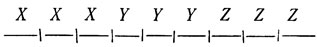
То, что это всегда будет так независимо от длины цепочки, видно из того, что:

• первая доля содержит ^N/₃ клеток,
• вторая доля содержит 2^N/₃ клеток.

Первый порог определяется отношением

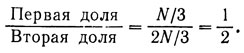
Аналогично второй порог определяется отношением

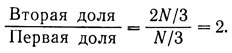
Покажем еще, как эта модель работает при другом N:

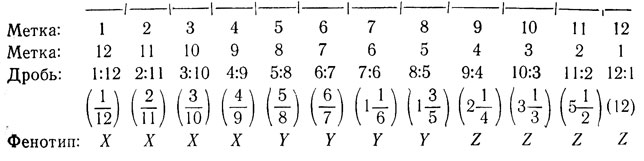
Аналогично если бы мы хотели, чтобы цепочка разделилась на четыре равные части, то пороги надо было бы взять такие:

Первый порог: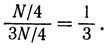

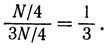
Второй порог: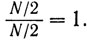

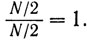
Третий порог: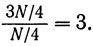

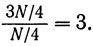
Тогда мы получили бы следующее: отношения, меньшие 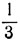, дали бы состояние W, отношения от 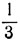до 1 дали бы состояние X, отношения от 1 до 3 дали бы состояние Y и отношения, большие 3, дали бы состояние 2.

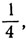
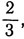
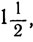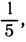
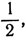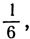
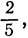
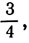
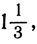
Аналогично, чтобы получилось пять равных частей, пороги, или критические значения, должны быть равны 4. Для шести равных частей: 1, 2, 5; для семи равных частей: 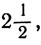6; и так далее.

Ясно, что этот способ можно обобщить на случай любого числа равных частей. Кроме того, ничто нам не мешает делить цепочку

и на неравные части. В случае деления, например, на три части ничто не мешает взять критические значения равными ⁵/₁₁ и 4 вместо 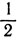и 2. Единственным ограничением здесь служит то, что если в цепочке будет меньше четырех клеток, то третий кусок исчезнет; отсюда вытекает интересный способ объяснения того, что по мере роста эмбриона в нем увеличивается число различных областей.

Хотя эти первые идеи неизбежно основаны на упрощенном варианте исследуемого явления, наша модель все-таки демонстрирует управление пространственной структурой, и оно основано на эффективных наборах инструкций. Справедливость требует отметить, что ни одной другой модели, обладающей тем же свойством, не предложено. Ближайшая к этой теме модель Роуза [4, 5] не описана эффективно, и не ясно, будет ли она действительно работать так, как предполагается.

По поводу этой модели управления пространственной структурой следует сделать ряд замечаний.

Более пятидесяти лет назад Т. Г. Морган [6] предложил различать два вида регенерации, которые он назвал "эпиморфоз" и "морфоллаксис". Под эпиморфозом он понимал регенерацию, происходящую путем вырастания новой массы ткани, которая затем оформляется в недостающую часть. Под морфоллаксисом он понимал такой случай, когда оставшаяся часть организма сама переформируется так, что превращается в целый организм. Можно пойти дальше и заметить сходство между этим различием и различием, которое можно провести между теми случаями в развитии, когда какая-то форма образуется путем роста в определенном направлении, и теми случаями, когда сначала происходит рост, а потом оформление.

Модель, предложенная здесь, очевидно, соответствует морфоллаксису, поскольку, если часть клеток удалить, то она их не возмещает, а изменяет оставшуюся часть, чтобы приспособиться к новой ситуации. (В этом смысле можно еще сказать, что растущие сети автоматов, наоборот, ближе к эпиморфозу, чем к морфоллаксису, поскольку там "форма" системы или сети определяется направлениями роста.)

Наша модель была бы ближе к системе, применяющей и эпиморфоз и морфоллаксис, если бы мы включили в нее регулятор размера, поддерживающий постоянную общую длину. Может быть, проще всего это было бы сделать так: придать одной из концевых клеток способность самовоспроизведения (пусть той, которая помечает себя числом +1); пусть она воспроизводится во внутреннем направлении каждый раз, когда получает от соседней клетки число, меньшее определенного критического значения, и делает это непрерывно, пока получает такое число. Если мы введем общее правило, что всякая клетка, помечающая себя +1, становится регулятором размера, то хотя наборы инструкций, данных всем клеткам, останутся одинаковыми и каждая клетка в принципе сможет стать регулятором размера, тем не менее регулятором во все моменты времени будет концевая клетка, а если ее отрезать, ее место автоматически займет следующая. Далее, если убрать все клетки, кроме регулятора размера, то эта оставшаяся клетка воспроизведет нужное число новых клеток. Результатом этого, если управление структурой тоже работает, будет то, что многие старые клетки на одном конце будут вынуждены изменить свой фенотип, чтобы дать место вновь воспроизведенным клеткам на другом конце.

Возможно, не лишен интереса тот факт, что, предприняв этот простой шаг, мы получаем систему, работа которой в некоторых отношениях похожа на функционирование гидры. Действительно, у гидры имеется гипостом, находящийся на дистальном конце тела, который, по-видимому, регулирует остальную часть организма (и если его удалить, то образуется новый гипостом в самом дистальном конце оставшейся части организма), и существуют Данные [7, 8], говорящие о том, что под гипостомом находится область роста, регулирующая его, и что рост в этой области во время регенерации "проталкивает" следующие клетки в области с другими фенотипами, которые они затем принимают. Это отнюдь не означает, что мы предполагаем, что гидра функционирует подобно нашей модели. Главное ее назначение в том, чтобы показать, как, добавляя, к описанной основной модели простые гипотезы, можно резко усложнить ее поведение в развитии; она может, таким образом, дать начало изучению возможных способов регуляции в живых организмах, поведение которых может быть очень далеким от того идеализированного поведения, которое мы берем за отправную точку.

Наша система управления пространственной структурой обладает еще одним достоинством, которое проявляется, если попытаться увеличить круг явлений, моделью которых она служит. Дело в том, что в ней есть не только уровень, на котором все клетки идентичны, и второй уровень, на котором они разбиваются на группы, но еще и третий уровень, характеризуемый дробями (т. е. отношениями двух меток), на котором все клетки различны. Это свойство было бы особенно полезно при моделировании явления, которое Голдейкр назвал явлением "разрывности" (см. гл. 3). Например, кожные клетки одной области, дающие волосяной покров, должны быть похожи, но, кроме того, отдельные клетки в пределах этой области должны дифференцироваться определенным образом с тем, чтобы одни клетки давали волосы, а другие нет.

Мы могли бы попытаться усложнить поведение этой модели посредством обобщения на случай пространственной, а не функциональной дифференцировки. Прежде всего мы могли бы спросить, какого рода инструкции нужны для того, чтобы объяснить регенерацию простых двумерных форм, например вида X или Y, как в предыдущей главе. Затем мы могли бы спросить, какие инструкции нужны для того, чтобы построить и содержать в исправности заданные формы, такие, как формы конкретных органов конкретных животных. Особенно примечательна в этой связи работа Д'Арси Томпсона [9], поскольку он показал, как можно изображать органические формы в двух измерениях, пользуясь прямоугольными координатами^*, и как затем их можно многообразно изменять, просто по-разному деформируя координатную сетку. В связи с его работой возникает мысль, что, возможно, форма одного и того же органа у разных животных развивается и поддерживается с помощью одинаковых инструкций и лишь с той разницей, что критические значения или пороги выбираются заново в каждом случае.

^* (Более подробно эти представления Д'Арси Томпсона вместе сих критикой изложены в книге Р. Розена "Принцип оптимальности в биологии", 1969, стр. 101-119.- Прим. ред.)

Одно из основных предположений описанной выше модели управления пространственной структурой состоит в том, что клетки на концах цепочки могут "узнать", что они действительно находятся на конце, чтобы начать весь процесс управления. Однако для наших целей достаточно заметить, что поверхностная клетка неизбежно отличается от внутренней клетки, поскольку она может вступать в общение с другими клетками только одной своей стороной. Поэтому поверхностная клетка может меньше подавляться другими клетками, чем внутренняя, и поэтому здесь может спонтанно начаться процесс, который в другом месте не может начаться. Следовательно, нет необходимости постулировать специфические влияния среды вопреки мнению Чайлда [10], который считает нужным это делать, чтобы объяснить начало подобного процесса.

Но, возможно, самая важная идея, заключенная в этой модели,- это идея двустороннего потока информации. Право, чем больше думаешь об этой проблеме, тем труднее представить себе, как можно было бы осуществить подобное управление, не реализуя так или иначе эту идею. В описанной здесь модели информация, передаваемая в каждом направлении,- это одновременно и "первичная" информация и обратная связь, и тем самым используется она очень экономно.

Поэтому имеет смысл спросить, нет ли данных, говорящих о наличии двусторонних потоков информации в организмах, в которых в данный момент происходит регуляция или регенерация. К сожалению, отсутствие таких двусторонних потоков в данном организме доказать вообще трудно. Но положительные свидетельства существуют в виде "двухградиентной" теории развития.

Эта теория была выдвинута впервые в работе Руннштрема. Проводя опыты с морским ежом [11], он высказал предположение, что вдоль оси яйца существуют не один, а два качественно различных градиента. Один из них анимальный, а другой вегетативный, и оба доходят до противоположного полюса, перекрывая друг друга на всем протяжении яйца. С тех пор накопилось много данных, говорящих в пользу этой теории, и им посвящен хороший обзор Гёрстадиуса [12], в котором сведены вместе данные, полученные путем изоляции и трансплантации тканей, химических исследований яйца, измерений метаболизма яйца и комбинаций этих методов. Ясно, что такой градиент (а это градиент скорости обмена веществ) может быть связан с потоком информации, и данные о существовании у морского ежа двух градиентов различных направлений в какой-то мере обнадеживают.

Здесь изучалась проблема совершенной регуляции и регенерации на моделях "совершенных" организмов. Однако не все организмы обладают такими возможностями: некоторые, например те, что развиваются из "мозаичных" яиц, обладают очень слабыми возможностями подобного управления. Вообще способность к регенерации больше у простых, чем у высокоразвитых видов, а регуляция легче проходит на ранних, чем на поздних стадиях развития. Огромное большинство организмов, конечно, обладает частичной способностью регуляции в указанном смысле, и круг применимости этой модели, следовательно, можно было бы увеличить, сделав те или иные ее части после того, как они развились, неизменяемыми или неподвластными ее управлению.

Но это, конечно, не означает, что на первых порах не имеет смысла заниматься моделированием регуляции и регенерации в их полном, совершенном варианте, как здесь и было сделано. Такая модель служит основой, к которой можно добавлять новые предположения, если только основная идея кажется достаточно перспективной.