Генетическая интерпретация модели

Одной из трудностей, связанных с описанной нами моделью, является то, что модель, очевидно, требует, чтобы каждая клетка была математиком, умеющим не только складывать, но даже делить. Это сводится, конечно, к тому, что каждая клетка должна уметь работать, как некая простая вычислительная машина или автомат, выход которого зависит в одном случае от абсолютной величины поданного входа, а в другом случае - от относительных величин двух входов.

Кибернетика может предложить множество различных систем, способных делать именно это. Эта задача в любом ее варианте не представляет ничего сложного для машины Тьюринга или вычислительной машины, имеющей соответствующую программу. Беда только в том, что это нам нисколько не поможет в решении вопроса, с которым мы рано или поздно столкнемся: как представить себе построенную модель в виде биологического процесса? Действительно, для этого нужно провести подобные вычисления на каком-то биологически более убедительном материале, чем машина Тьюринга. То есть требуется модель, которая бы показала, как действительно клетка может прибавить постоянное число к какому-то ее входу и дать сумму на выход или как отношение двух каких-то входов может определять поведение клетки, и все это должно опираться только на известные или хотя бы правдоподобные формы клеточной активности.

Ближайшую возможность к этому нам предоставляет работа Жакоба и Моно и круг их идей о генах-регуляторах, операторах и оперонах [13], и, опираясь на эти понятия; они сами построили много моделей дифференцировки в своей работе о "телеономических" механизмах в процессах клеточного обмена, роста и дифференцировки [14]. (См. краткое описание этой работы в приложении 4.)

Мы теперь займемся обобщением моделей Жакоба и Моно с тем, чтобы объяснить пересчет клеток и зависимость их поведения от отношения входов. Но для этого с самого начала следует явно высказать ряд предположений. Все эти предположения либо присутствуют явно в работе Жакоба и Моно, либо совместимы с их идеями. Вот они:

1. Скорость, с которой ген функционирует, и, следовательно, скорость, с которой образуется продукт, синтез которого этот ген в конечном счете контролирует, есть функция количества или концентрации вещества, активирующего его или подавляющего его активность. Действие этого правила ограничено следующим:
2. Существует максимальная скорость, с которой каждый ген может функционировать, и, следовательно, максимальная скорость, с которой может происходить синтез соответствующего продукта. Эта скорость может меняться известным образом от гена к гену внутри одной клетки, но должна быть одинакова для одинаковых генов разных клеток.
3. Действия на ген различных корепрессоров суммируются.
4. Репрессор может инактивироваться рядом различных продуктов, действия которых на репрессор на этот раз тоже суммируются. Инактивация репрессора происходит не по закону "все или ничего", а зависит от количества или концентрации инактивирующих продуктов.
5. Скорость, с которой данный ген-регулятор продуцирует свой репрессор, постоянна для этого гена и обычно не может быть изменена никаким сигналом, посланным этому гену. Таким образом, это является исключением из правила 1.
6. Химическая взаимосвязь между генами специфична:

   Конкретные особенности каждой регуляторной системы мы получим, 
   если сделаем предположение о самом типе данной специфической 
   взаимосвязи. Подобные гипотезы вполне допустимы, поскольку, 
   как мы уже видели, специфичность индукции репрессии и 
   аллостерического подавления основана не на каком-либо химическом 
   принципе аналогии, а является всецело результатом отбора 
   наиболее эффективных механизмов регуляции [15].
   

7. Первичные продукты деятельности генов недолговечны. Добавим к этим предположениям правило, реализуемое произвольно, что всегда, когда степени репрессии и активации теоретически равны, преобладает репрессия. То есть активация должна превзойти репрессию по силе, чтобы оказать свое действие.

Опираясь на эти правила, вернемся к нашей проблеме и, поскольку сложение представляется более простым процессом, чем деление, обратим сначала наше внимание на пересчет.

В сущности для пересчета нужно, чтобы каждая клетка в цепочке вырабатывала стандартное вещество с большей скоростью, чем это делала предыдущая клетка. Тогда меткой каждой клетки будет служить скорость, с которой она производит это вещество, и если выходом каждой клетки служит это вещество, одновременно являющееся входом следующей клетки, то остается только сделать так, чтобы каждая клетка преобразовывала скорость входа в скорость выхода с усилением, и пересчет готов. (Желательно, чтобы усиление было постоянным для всех клеток, т. е. чтобы каждый раз прибавлялось одинаковое количество.)

Это можно сделать несколькими способами. В каждом из них используется тот факт, что если одним из выходов каждой клетки является вещество, частично инактивирующее репрессор, производимый регуляторным геном следующей клетки, то достаточно, чтобы количество этого вещества, в свою очередь определяемое степенью инактивации репрессора, возрастало, чтобы пересчет, как он описан выше, был возможен.

1. Подходящая зависимость выхода от входа для oперона. Простейшее и в то же время наиболее подходящее к данному случаю решение этого вопроса состоит в следующем.

Определенная степень инактивации репрессора вызовет определенную активность операторного гена, которая в свою очередь создаст определенный уровень активности в каждом структурном гене, связанным с ним. Теперь если один из этих структурных генов продуцирует вещество, частично инактивирующее репрессор той же самой регулятор-оперонной группы в следующей клетке (и репрессор его собственной регулятор-оперонной группы был частично инактивирован таким же способом), то остается только позаботиться о том, чтобы график зависимости степени инактивации репрессора от скорости синтеза вещества, инактивирующего репрессор, был таким, чтобы в результате получилась большая степень инактивации репрессора следующей клетки, чем предыдущей; и тогда пересчет возможен. Иными словами, для каждого такого оперона Выход = Вход + Константа, где константа такова, что без ее прибавления каждый оперон работает с той же скоростью, что и оперон предыдущей клетки. Тогда, если каждую клетку охарактеризовать скоростью работы того структурного гена, о котором мы говорим, мы получим пересчет клеток по этим скоростям.

2. Более одного структурного гена. Другая простая идея состоит в том, что оперон в каждой клетке содержит более одного структурного гена, причем каждый из них независимо вызывает производство вещества, частично инактивирующего репрессор следующей клетки. Пусть, например, в каждый оперон входят два структурных гена, каждый из которых производит указанное вещество со скоростью, пропорциональной степени активации его оператором. Пользуясь диаграммным языком Жакоба и Моно [14], это положение можно изобразить так:

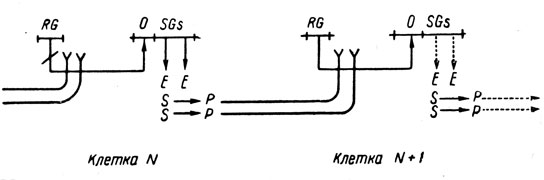
Недостаток этой модели состоит в том, что каждый раз происходит скорее умножение (в данном случае на 2), чем сложение. Конечно, для пересчета можно было бы использовать и умножение, но это привело бы к усложнению модели двусторонней передачи информации и, кроме того, после небольшого числа таких передач репрессор скоро был бы полностью инактивирован и пересчет прекратился бы.

3. Положительная обратная связь. Возможно, наиболее удовлетворительное решение заключается в устройстве положительной обратной связи внутри каждой клетки так, чтобы один из структурных генов, входящих в оперон, заведовал выработкой вещества, частично инактивирующего репрессор, действующий на сам оперон. Тогда от клетки к клетке будет постепенно увеличиваться количество вещества, частично инактивирующего репрессор, образованный регуляторным геном следующей клетки.

Это можно изобразить следующей схемой:

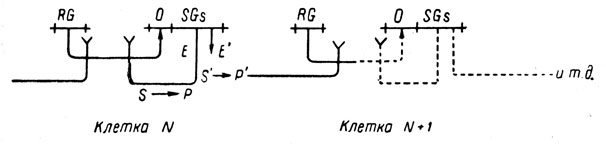
Это всего лишь обобщение той идеи об обратной связи, которой пользуются сами Жакоб и Моно (модель II [16]).

Вряд ли нужно описывать эту простую систему с помощью дифференциальных уравнений, чтобы показать, что дна работает, но надо сделать следующее замечание.

Максимальная скорость, с которой самовозбуждающийся структурный ген может работать, должна быть как можно ниже. Если бы такой максимальной скорости не было, то все клетки "закусив удила" продолжали бы все сильнее и сильнее инактивировать свои репрессоры, пока совсем их не подавили, и никакой дифференцировки бы не произошло.

Прежде чем перейти к делению, надо сделать несколько замечаний, касающихся всех трех способов осуществления пересчета.

Для того чтобы процесс мог начаться, требуется некоторая минимальная степень инактивации репрессора в начале цепочки.

Если часть клеток удалить, или добавить новые, или поменять их местами, то пересчет заново происходит автоматически, поскольку он выражается в динамическом равновесии, и метки никогда не ставятся окончательно - это просто скорости вырабатывания некоторого вещества.

Сколько клеток вся система может таким способом пересчитать, зависит от соотношения между силой действия репрессора и силой действия тех веществ, которые его инактивируют; чем больше разница между ними, тем больше клеток можно будет пересчитать, прежде чем репрессор будет полностью инактивирован. Вот почему максимальная скорость работы структурного гена должна быть как можно меньше.

Задача здесь такая. У нас есть черный ящик ровно с двумя входами. Их можно называть "количество вещества Л" и "количество вещества В" соответственно. Ящик имеет N выходов, из которых в каждый момент времени работает только один. Какой из них работает - это зависит от отношения величин входов. Какая модель типа Жакоба и Моно может обладать таким поведением?

Проблема в сущности не так сложна, как кажется t первого взгляда. Уже одна из моделей, предлагаемых в работе Жакоба и Моно, а именно модель III [17], после небольшой переделки обладает поведением, зависящим от отношения входов. Эта модель демонстрирует явление, которое Жакоб и Моно называют "перекрестной обратной связью", и состоит из двух регулятор-оперонных блоков, соединенных таким образом, что если один из них работает производительнее, чем другой, то он его полностью подавляет, и продукция всей системы определяется структурными генами первого блока. Активность каждого из этих блоков определяется наличием или отсутствием соответствующих веществ. Вот схема этой модели:

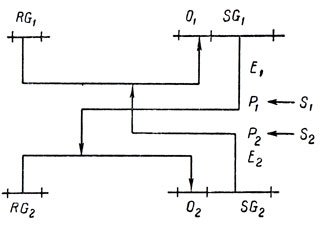
Эту взаимосвязь можно выразить и так: если то, что частично инактивирует репрессор, действующий на RG₁, сильнее, чем то, что в то же самое время частично инактивирует репрессор, действующий на RG₂, то продуктом всей системы становятся продукты структурных генов, управляемых RG₁, а не продукты структурных генов, управляемых RG₂, и, наоборот, если сильнее то, что частично инактивирует репрессор, действующий на RG₂, то вырабатываются только продукты структурных генов, управляемых RG₂. (Предполагается, что одна и та же сила соответствующего инактивирующего вещества заставляет структурные гены обеих систем продуцировать одинаковые количества корепрессоров. Ясно, что можно положить по определению равными такие количества инактивирующих веществ, которые приводят к синтезу корепрессоров равной силы.)

Здесь мы имеем простейший случай, когда отношение входных веществ определяет поведение системы. Теперь нужно только сделать так, чтобы веществами, инактивирующими репрессоры, были вещества, продуцируемые регулятор-оперонными блоками попутно в ходе пересчета, как он описан выше (таким образом, эти вещества теперь влияют одновременно на пересчет и вычисление дроби в следующей клетке), и мы получим цепочку, разбивающуюся на две равные области по принципу двустороннего потока информации. Каждая клетка этой цепочки, конечно, должна при этом состоять из двух блоков пересчета, соединенных с соответствующими блоками двух соседних клеток (по одному на каждое направление), и двух регулятор-оперонных блоков, соединенных между собой, как описано выше, и вычисляющих отношения.

Для полноты картины следует сказать, что во всех подобных ситуациях, видимо, установление нужного фенотипа требует лишь определенного количества определенного вида белка, тогда как в описанной таким образом модели производство фермента для этого белка непрерывно изменяется. Но эта трудность не принципиальна, и с ней можно справиться несколькими способами. Например, мы можем постулировать, что, после того как накопится достаточное количество этого белка, оно запирает дальнейший его синтез. Это запирание не должно мешать работе других структурных генов, находящихся в одном опероне со структурным геном, отвечающим за выработку фермента для этого белка, так что ферменты, нужные для выработки вещества, подавляющего другой регулятор-оперонный блок, будут по-прежнему вырабатываться и оказывать свое действие. В этом случае для того, чтобы изменения состояния клетки были обратимыми, надо еще предположить, что белки, определяющие фенотип, могут разрушаться веществами, производимыми другим опероном.

Более удовлетворительная возможность состоит в том, что существует некоторая обратная реакция, которая всегда стремится разрушить образовавшийся белок. Тогда, чтобы поддерживать заданный уровень этого белка, надо либо непрерывно его синтезировать, чтобы возместить убыток, либо непрерывно синтезировать вещество, способное инактивировать вещество, обусловливающее обратную реакцию. Такой способ больше соответствует работе остальной системы, в которой первые продукты деятельности генов мы условились считать короткоживущими, что делает необходимым непрерывное производство их для поддержания постоянного уровня. Если эти белки будут короткоживущими по причине такой обратной реакции, то общее состояние клетки будет легко изменяться на противоположное при перемене местами скоростей притока входных веществ А и В.

Однако этот вопрос не является центральным в настоящем обсуждении; коль скоро мы увидели, что эта трудность преодолима, нет никаких причин упоминать об этой части системы при обсуждении следующих моделей, особенно если учесть, что это только усложнит картину.

Легко видеть, что от этой модели только один шаг к модели, в которой цепочка разбивается на две неравные части. Пусть мы хотим, например, чтобы цепочка разбилась на два куска - в одну треть и в две трети ее длины. Тогда для этого надо, чтобы одного из веществ в данной клетке, пусть вещества A, было хотя бы вдвое больше, чем вещества В; иначе эта клетка будет второго типа.

Это можно сделать многими способами. Один из них состоит в допущении, что RG₁ (или SG₁ или Е₁) имеет вдвое меньшую мощность, чем RG₂ (или SG₂ или Е₂), и, следовательно, вещества А должно быть вдвое больше, чем вещества В, чтобы RG₁ начал пересиливать RG₂.

Возможность, менее подходящая для данного случая, заключается в том, что RG₂ посредством оператора управляет опероном, содержащим не один, а два структурных гена, которые вместе производят вдвое больше энзима для производства корепрессора, чем каждый из них в отдельности, и, следовательно, RG₂ вдвое сильнее подавляет O₁. Это можно изобразить следующей схемой:

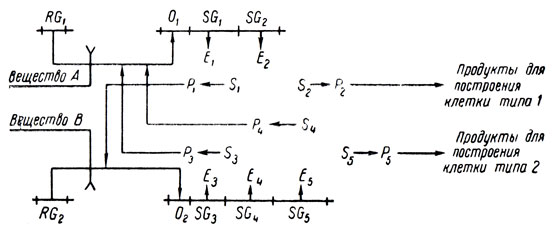
Очевидно, эта модель обобщается на случай любой дроби.

До сих пор мы говорили только о системах с двумя выходами. Теперь займемся случаем, когда возможны три типа клеток и цепочка разбивается на три равных куска клеток этих типов. Этого можно достигнуть с помощью следующей модели:

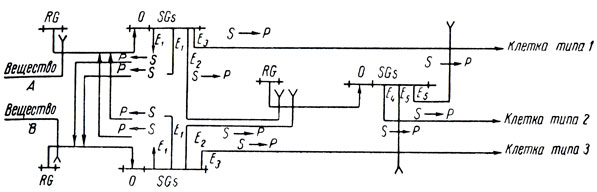
Чтобы она работала правильно, нужно добавить, что репрессор, действующий на блок, который производит белки для клеток типа 2, может инактивироваться лишь совместным действием веществ, производимых двумя другими блоками, но не каждым из них в отдельности. Назовем это "конъюнктивной" индукцией в противоположность "дизъюнктивной" индукции. Тогда модель работает следующим образом: если вещества А хотя бы вдвое больше, чем вещества В, то блок, соответствующий типу клеток 3, будет подавлен блоком клеток типа 1, а репрессор блока клеток типа 2 не будет инактивироваться, так как, согласно только что сказанному, для того, чтобы его инактивировать, требуется совместная работа блоков клеток типа 1 и 3. Поэтому клетка в целом станет клеткой типа 1. Аналогично если вещества В хотя бы вдвое больше, чем вещества А, то клетка в целом будет синтезировать белки, определяющие тип 3. Если же отношение количеств этих веществ заключено между ¹/₂ и 2, то возникнет равновесие, при котором оба блока клеток типов 1 и 3 будут частично работать. Тогда заработает блок клеток типа 2, а это приведет к подавлению производства белков, определяющих типы 1 и 3 (но не веществ, индуцирующих блок клеток типа 2), и в результате клетка станет клеткой типа 2.

Общая схема модели разбиения на три равных куска, основанной на принципах Жакоба и Моно, такова:

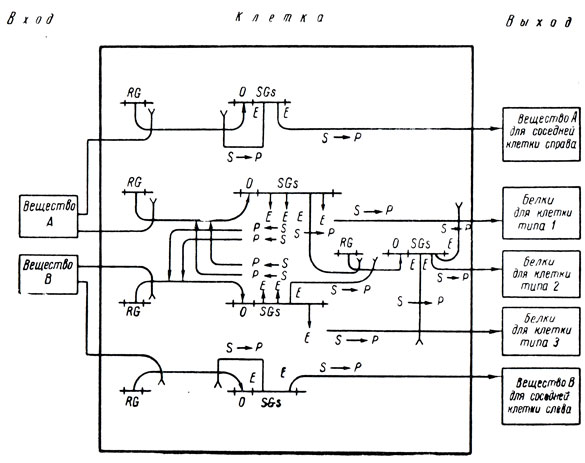
В начале этого параграфа было сказано, что для моделирования управления структурой требуется что-нибудь биологически более убедительное, чем, скажем, машинная программа. Однако, показав, что схематизация Жакоба и Моно позволяет реализовать нужные соотношения между входами и выходами для каждой клетки, стоит подумать и о том, нет ли более подходящего и красивого способа выразить идеи Жакоба и Моно, чем в виде тех неизбежно несколько нескладных соглашений, которые они приняли. Действительно, может быть, лучше, если бы мы решили попытаться изучать более сложные системы, рассматривая регулятор-оперонный блок как черный ящик с определенными взаимоотношениями между входом и выходом, соответствующими нашим представлениям о работе этого блока, а не описывая в точности каждый шаг работы всех его составных частей.

Поскольку модели Жакоба и Моно - в сущности сети, в которых эти блоки различным образом взаимосвязаны, возможно, стоило бы исследовать много сетей, уже известных в кибернетике, чтобы посмотреть, не могут ли они заменить сети Жакоба и Моно. Сугита [17, 18], например, показал уже, как выглядят модели Жакоба и Моно в переводе на язык логических сетей.

Возможно также, что при этом могут пригодиться не только конечные, но и бесконечные автоматы, и, следовательно, может оказаться полезной работа Стала и Гоэна о представлении биохимических явлений машинами Тьюринга [19].