6-2. Вероятностное определение количества информации по Шеннону

Как правило, при приеме по телеграфу после первых слов можно с достаточной точностью предсказать следующие слова. Поэтому говорят о взаимосвязи элементов в сообщении. Связь понимается в вероятностном смысле, т. е. существует условная вероятность появления (при данном алфавите) символа А вслед символу В:

Так, в русском тексте после гласной не может следовать мягкий знак или подряд четыре гласные буквы, т. е. условная вероятность равна нулю. Если понятно, какие символы последуют дальше, сообщение представляет мало интереса и содержит меньше информации, чем оно содержало бы, если бы взаимная связь его элементов не была очевидна. В качестве примера взаимных связей можно привести прямой порядок слов в предложении, согласно которому после подлежащего должно следовать сказуемое: если принимается сообщение "Весна пришла", то достаточно принять "Весна при..." и прием следующих символов уже не добавит информации. Это свойство сообщений характеризуется величиной, называемой избыточностью.

Количество информации может уменьшаться также из-за того, что в силу особенностей языка различные символы с разной вероятностью появляются в тексте сообщения. Так, на 1000 букв приходится следующее количество повторений:

Так, свойство буквы Е в английском языке встречаться чаще буквы I позволяет предсказывать, предопределять сообщение, т. е. неравно- вероятное, неравномерное появление символов в сообщении (если, конечно, оно заранее известно) уменьшает количество сведений, количество информации в принимаемом сообщении.

Современный развитый язык насчитывает в своем составе до 100 тыс. слов. Однако не все они одинаково часто употребляются. В среднем достаточно знать несколько тысяч слов, чтобы изъясняться. Слова в языке также обладают разной вероятностью появления. Очевидно, что неравномерное распределение вероятностей появления отдельных слов в языке (максимум одних и минимум других) также уменьшает количество информации, так как можно предсказать появление тех или иных слов в сообщении.

Так же как в теории вероятностей, в теории информации к вероятности возможны два подхода. В первом случае, который эквивалентен усреднению по времени, рассматриваются бесконечно длинные (а практически просто длинные) сообщения. В процессе наблюдения во времени за длинным сообщением исследуется статистика появления отдельных символов или их комбинаций. Во втором случае рассматривается множество (теоретически бесконечно большое) конечных сообщений и статистические характеристики определяются путем усреднения по ансамблю сообщений. При этом всегда предполагается, что число сообщений (или символов) такое большое, что применим закон больших чисел. Приведем простейший вывод выражения для количества информации, предполагая отсутствие связей элементов. Пусть имеем алфавит, состоящий из m элементов (символов) h₁, h₂, ..., h_i, ..., h_m. Вероятности появления этих элементов в сообщении соответственно равны р₁, р₂,... ..., p_i, ..., р_m. Составим из этих элементов сообщение, содержащее n элементов. Среди них будет их элементов h₁, n₂ элементов h₂, ..., n_m элементов h_m. Вероятность появления каждой комбинации из n элементов выразится произведением вероятностей отдельных элементов, так как предполагается, что появление каждого элемента есть независимое событие. С учетом повторяющихся элементов вероятность некоторого сообщения

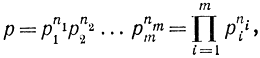
вероятность появления i-го символа

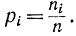
Можно считать, что все N возможных сообщений (все перестановки) равновероятны. Поэтому

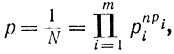
откуда число возможных сообщений

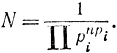
Логарифмируя, получаем количество информации в сообщении длиной n при неравновероятности его элементов:

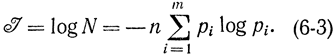
Можно дать другой вывод этой формулы. Число сообщений можно записать в виде

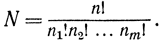
В данном случае предполагается, что число элементов в сообщении n всегда больше числа символов в алфавите m, n>m. Кроме того, считается, что в сообщении присутствуют все символы алфавита (хотя бы с малой вероятностью). В этом состоит основная особенность вероятностного рассмотрения. Поэтому общее число сообщений может быть найдено как число возможных перестановок n элементов n!. Однако из этого количества следует исключить число перестановок одинаковых между собой символов, которое равно:

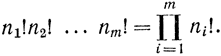
По формуле Стирлинга при n большом

Эта формула дает хороший результат при n> 100. С другой стороны,

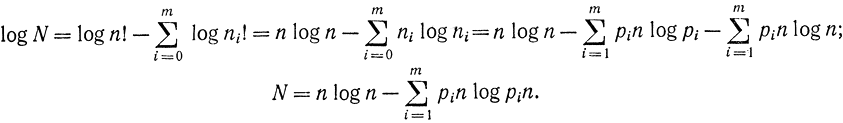
Учитывая, что

получаем

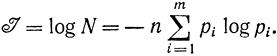
Пример 6-2. Имеются символы а, в, с. В этом случае m=3, n₁=2, n₂=3, n₃=1, "=24-3+1=6. Возможные сообщения будут выглядеть следующим образом: 1 - аааввс; 2 - ваавввс; 3 - вваас; 4 - ввваас; ... Общее число сообщений

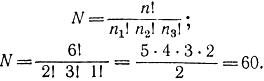
Отсюда при длине сообщения n=6 количество информации будет равно:

Из формулы (6-3) нетрудно получить формулу (6-2) для случая равновероятных событий, надо только положить все p_i=1/m. Если вероятность какого-нибудь элемента равна единице, а остальных нулю, то количество информации равно нулю, так как очевидно, что никакой информации сообщение не имеет, т. е. в этом случае заранее известно, что придет символ, вероятность которого равна единице. Наоборот, в случае p_i=1/m ситуация наиболее неопределенная и сообщение содержит максимальное количество информации.

Возможность выбора и уникальная атмосфера сайта https://sterlitamaksm.com помогут вам организовать незабываемое свидание с девушкой в Стерлитамаке.