16-1. Математическая формулировка задачи

Математически задача линейного программирования ставится следующим образом: ищется максимум линейной формы (функции цели)

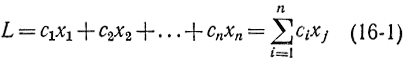
при условиях

или

Словесно задачу линейного программирования можно сформулировать так: требуется найти максимум линейной формы от n переменных при m ограничениях в виде неравенств или равенств. Нетрудно убедиться, что всегда можно говорить только о равенствах, так как введением дополнительных или слабых переменных x_n+v, (c=1,...,p≤m) неравенства всегда можно свести к строгим равенствам. Так, ограничение

можно свести к равенству, добавив переменную x_n+1:

Тогда условие (16-2) сведется к (16-3) и условию не отрицательности переменной x_n+1. Поэтому можно сказать, что при решении задачи линейного программирования определяются такие значения n переменных x_j, которые бы обращали в максимум линейную форму

при условии выполнения m равенств