16-3. Геометрическая интерпретация задач линейного программирования

В решении задач линейного программирования часто пользуются геометрическими интерпретациями в разных вариантах.

Система неравенств (16-2) определяет в пространстве x₁,...,x_n выпуклую область - выпуклый многогранник или многоугольник. Для простоты рассмотрим случай для n = 2 переменных:

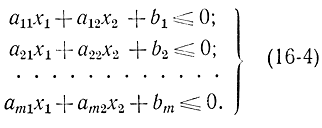
Каждое из этих соотношений определяет область, лежащую по одну сторону от прямой:

Выпуклой называется такая область G векторной переменной x, для которой справедливо следующее свойство: если из любых двух значений векторов х¹ и х², принадлежащих этой области (х¹∈G, х²∈ G), образовать выпуклую линейную комбинацию

где λ - произвольное действительное число, для которого 0≤λ≤1, то вектор х³ также будет принадлежать этой области: х³ ∈ G.

На рис. 16-1 изображены выпуклая и не выпуклая области значений х¹ и х²; Действительно, если на рис. 16-1, б выбрать точку х³, равную линейной комбинации точек х¹ и х², то она не будет принадлежать заштрихованной области, и поэтому эта область не будет выпуклой. С другой стороны, нетрудно убедиться, что для любых двух точек, принадлежащих заштрихованной области на рис. 16-2, я, выполняется условие (16-5), и поэтому эта область является выпуклой.

Линейная форма (16-1) в случае двух переменных принимает вид

Это - уравнение прямой в плоскости (x₁, x₂), пересекающей оси x₁ и x₂ в точках L/c₁ и L/c₂ соответственно (рис. 16-2). Величины c₁ и c₂ определяют наклон прямой (угол наклона к оси x₁ задается формулой 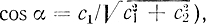, L определяет расстояние от начала координат до прямой, которое находится из формулы 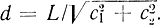. Теперь можно дать геометрическую интерпретацию задачи линейного программирования. Если требуется определить такие x₁ и x₂, которые придали бы линейной форме минимальное значение, то геометрически это означает, что необходимо провести прямую L (16-6), проходящую хотя бы через одну точку области и имеющую минимальное расстояние d от начала координат (рис. 16-3, а). В случае максимизации это расстояние должно быть максимальным (рис. 16-3, б). Могут представиться два варианта: прямая имеет с допустимой областью G. одну общую точку в вершине области или совпадает с Одним из ее ребер. Во втором варианте (рис. 16-4) имеет место вырожденный случай, т. е. линейная функция цели совпадает с левой частью одного из ограничений.

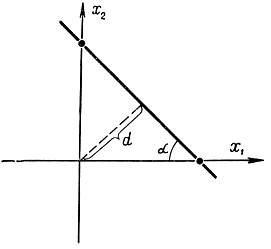
Рис. 16-4. Геометрическая интерпретация линейной функции цели

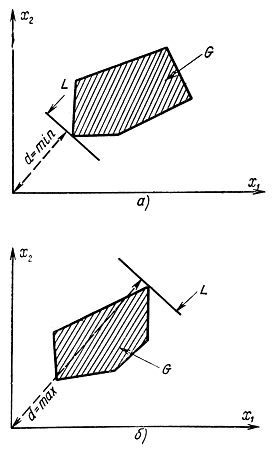
Рис. 16-4. Геометрическая интерпретация задачи линейного программирования для случаев минимума (а) и максимума (б)

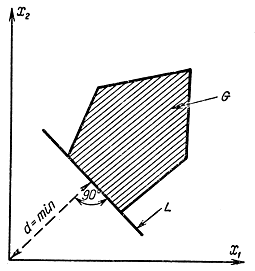
Рис. 16-4. Геометрическая интерпретация задачи линейного программирования для вырожденного случая