День 3. Оптимальное производственное планирование (Винерит или колмогорит? А может, то и другое?)

- Каковы ваши творческие планы?
- Еще не готовы, оптимизирую их на ЭВМ.

(Разговор о союзе композиторов)

На N-ском комбинате стройиндустрии заканчивалось производственное совещание.

- Итак, принимается без поправок оптимальный по прибыли производственный план на будущий год, который выдала ЭВМ. Возражений нет? - спросил директор.

- А нельзя ли поискать план получше? - раздался голос. - Машина машиной, но как бы не того... разобраться надо.

Законное желание! Попытаемся его удовлетворить.

Допустим, появились два новых строительных материала, которые в ознаменование успехов математики в строительстве решено назвать (в честь двух виднейших математиков современности, внесших вклад в кибернетику, Н. Винера и А. Н. Колмогорова) винеритом и колмогоритом. Оба материала одинакового качества, но один принесет комбинату прибыль 5 руб, за кубометр, а второй -6 руб.

- Все ясно! Выпускаем колмогорит, он прибыльней! - раздался нетерпеливый голос. Стоп! Не поддавайтесь на эту удочку: видимо, из-за кажущейся простоты решения подобных проблем и случилось так, что метод оптимального планирования производства советский математик Л. В. Канторович предложил только в 1939 году. Ведь ничего особенно сложного в этом методе нет, чтобы в нем не разобрался, скажем, Архимед. А интегральное исчисление, известное уже триста лет, куда мудренее, но кажущаяся очевидность мешала сделать до поры до времени следующий шаг. Итак, задача нетрудна, но все-таки она чуточку сложнее, чем представляется обладателю нетерпеливого голоса.

Пусть винерит должен выпускаться в количестве х₁, а колмогорит - в количестве х₂. Тогда общая прибыль П, которую принесут предприятию оба вида материала, выразится так

И план нужно построить таким образом, чтобы эта общая прибыль была максимальна. Отсюда...

Ну и что? - прервал нас нетерпеливый голос. - Задача стала еще абсурднее: если устремить х₁ или х₂ - все равно что - к бесконечности, то получим бесконечную прибыль.

Верно, в задаче чего-то не хватает. Но чего? Догадаться нетрудно. Даже если спрос на материалы неограничен, произвести их в неимоверном количестве обычно не удается: не хватает Ресурсов!

Всякое производство потребляет ресурсы, причем обычно несколько десятков видов, не меньше. И наши материалы не составляют исключения. Какие же ресурсы нужны для производства материалов? Вот они, в этой таблице.

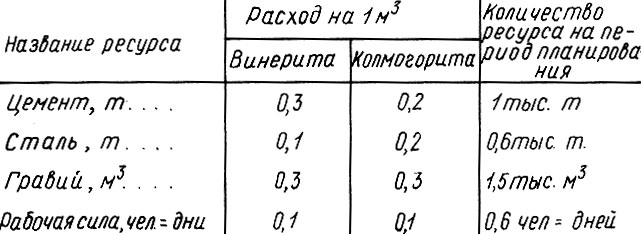
Как уже говорилось, обычно количество видов ресурсов составляет несколько десятков. Специфика наших материалов в том, что для них употребляется лишь четыре вида ресурса: чтобы понять суть, этого достаточно. Итак, для винерита и колмогорита нужны в разных количествах цемент и сталь (они измеряются в тоннах), гравий (чтобы читатель не подумал, будто ресурсы можно измерять только в тоннах) и рабочая сила (чтобы читатель почувствовал, насколько разнообразны могут быть ресурсы). В двух столбцах таблицы проставлены расходы каждого ресурса на производство одного кубометра каждого материала. Скажем, один кубометр винерита требует 0,1 т стали и 0,3 м³ гравия. В последнем, правом столбце, указано количество ресурса, которым располагает предприятие на планируемый период (скажем, на год).

А теперь составим ограничения по ресурсам. На один кубометр винерита идет 0,3 т цемента, а на х₁ кубометров пойдет в х₁ раз больше, то есть 0,3х₁ тонн. В свою очередь, колмогорит потребует 0,2 х₂ тонн цемента. Общее количество цемента, которое уйдет на оба материала, не должно превышать допустимого, 1 тыс, тонн, то есть

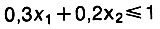
(чтобы не писать много нулей, давайте условимся все мерить в тысячах - и результат получим в тысячах кубометров). Такие же ограничения потребуются для стали, гравия и рабочей силы:

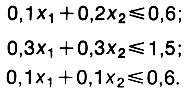
Сюда нужно добавить еще два ограничения-неравенства

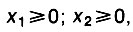
поскольку в любом случае наша цель состоит в производстве материалов, а не в их уничтожении.

Итак, требуется найти х₁ и х₂, которые доставляют максимум прибыли П (она называется целевой функцией задачи) при ограничениях на ресурсы. Отметим, что целевая функция П и ограничения линейны, то есть включают неизвестные х₁ и х₂ только в первой степени с постоянными коэффициентами. Эта математическая задача называется задачей линейного программирования. Линейное программирование часто возникает там, где речь идет об управлении сложной системой, нередко оно будет появляться и на наших страницах. Поэтому, из уважения к труду наборщиков обозначим его начальными буквами - ЛП.

- Прошу слова! - вмешался обладатель нетерпеливого голоса. - Вы хотите искать максимум функции П, но ведь линейная функция экстремума не имеет.

Точно! Не имеет: мы это знаем из школы. Ну хотя бы для случая одной переменной, когда у = х. Эта функция имеет вид, показанный на рис. 4, и у нее действительно нет экстремума, ни минимума, ни максимума. Но добавим сюда ограничение х₁≤5. Графически оно будет обозначать, что допустимые значения лежат левее прямой х = 5 (рис. 5). Подштрихуем прямую х = 5 со стороны допустимых значений и убедимся, что максимум функции у тогда достигается в точке А. Вот, оказывается, в чем дело: максимум линейной функции всегда лежит на границе допустимой области.

Для решения задачи ЛП Л. В. Канторович разработал свой метод. Наибольшую популярность при решении задач ЛП приобрел так называемый симплекс-метод, который предложил в 1948 году американский математик Данциг.

Мы не станем утруждать читателя изложением этого метода, да это и не очень нужно: если задача ЛП составлена, решить ее можно на ЭЦВМ с помощью стандартных программ. Важнее понять, в чем смысл решения задачи, тем более что для двух материалов решение можно получить совсем простым путем, графически.

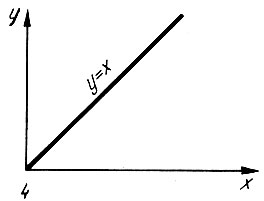
Рис. 4

Рис. 5

Для этого дадим графическое истолкование ограничениям по ресурсам. Рассмотрим первое ограничение, переписав его в форме равенства

Вот тут неизбежно придется вспомнить геометрию: прямую, описываемую этим уравнением, удается построить, если найти две ее точки. Проще всего - точки, в которых она пересекает оси координат. Положив х₁ = 0, получаем 0,2 х₂ = 1 или х₂ = 5, а положив х₂ = 0, получаем х₂ = 3,33. Проведя прямую через две точки с такими координатами, приходим к рисунку 6. Но это пока еще не то, что нам надо: ведь нас интересовало неравенство. Чтобы перейти от уравнения к неравенству, заметим, что последнему удовлетворяют все точки, лежащие ниже прямой. Подштрихуем эту прямую снизу (рис. 7). Поступая точно так же со всеми неравенствами, можно получить графический образ всех остальных ограничений (рис. 8).

Всмотревшись в этот рисунок, можно заметить, что не все линии на нем существенны. В самом деле, из рисунка видно, что если будет выполняться ограничение по цементу, то заведомо будут выполняться и ограничения по гравию и по рабочей силе, и поэтому их можно убрать. Правда, выполнение ограничения по стали при этом не гарантируется, и на участке АВ его придется сохранить. И вообще существенны лишь ограничения в виде многогранника ОВАС, который образует область допустимых значений переменных х₁ и х₂. Иначе говоря, каждая точка из этой области своими координатами определяет какой-либо допустимый производственный план. Но какой из этих планов даст максимальную прибыль?

Чтобы ответить на этот вопрос, обратимся к графическому изображению функции прибыли П. Построим сначала линию, вдоль которой прибыль П равна нулю, П - 5х1+6х2±О. Положив x₁ = 0, получим х₂ = 0, то есть эта прямая проходит через начало координат. Чтобы найти вторую точку прямой, положим x₁ = 1, откуда х₂ = -5/6. Изобразим эту прямую на рис. 9 вместе с допустимой областью. На этой прямой лежит один допустимый план x₁ = 0 и х₂ = 0. Однако такой план вряд ли устроит кого-либо, кроме завзятых лодырей. Их мы не рассчитываем встретить среди наших читателей, ибо лодыри предпочитают чтиво полегче, чем мы можем им предложить. Но случай П = 0 по-своему полезен и нам, и вот почему. Представим себе прямую, где П = 100. Не будем строить ее в точности, а лишь заметим, что она параллельна прямой П = 0 (ведь угловые коэффициенты у них одни и те же) и пройдет где-то намного правее и выше этой прямой. Таким образом, если увеличивать прибыль, то соответствующая ей прямая будет параллельно самой себе перемещаться вверх и вправо, или иначе на северо-восток. И требуется найти то предельное положение прямой, при котором она еще пересекает допустимую область ОВАС. Из чертежа видно, что это точка А с координатами х₁ = 2, х₂ = 2, то есть оптимальный план заключается в производстве 2000 м³ винерита и 2000 м³ колмогорита. Этот план принесет прибыль в П = 5x₂ ±6x₂ = 22 тыс. руб. Этот способ отыскания оптимальной точки допускает простую географическую интерпретацию. Пусть имеется местность, повышающаяся с юго-запада к северо- востоку, а прямые П = const - ее горизонтали, так что отметка местности выражает прибыль. На этой местности имеется четырехугольный участок ОВАС, на котором нужно расположить телебашню. Где вы ее поставите? Разумеется, в точке А, где повыше отметка местности.

Из чертежа видно, что если не производить винерит (х₁ = 0), то удастся произвести 3000 м³ колмогорита (х² = 3). Это принесет прибыль П = 5x₀ + 6x₃ = 18 тыс. руб. Итак, верхоглядное решение чуть не стоило нам 4000 руб. прибыли! А сколько прибыли уже потеряно из-за такого рода скоропалительных решений!

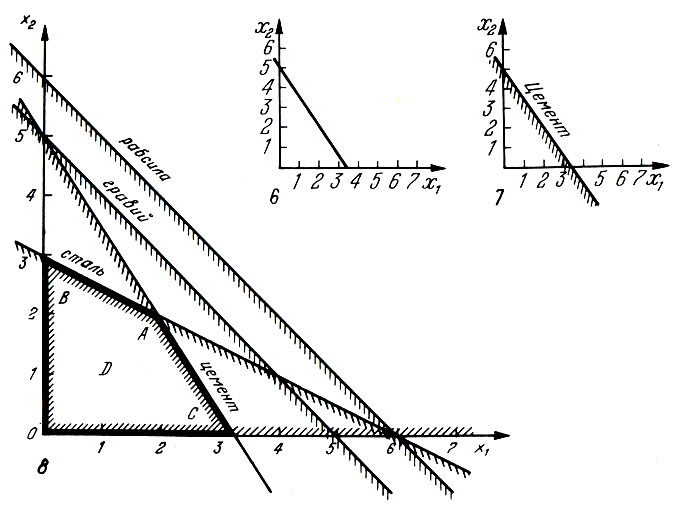
Рис. 6-8

Рис. 9

Способ, подобный описанному нами, возможен лишь для двух видов материалов. На N-ском комбинате строй индустрии их выпускается намного больше. Но решение, которое выдала машина, обладает той же особенностью - оно доводит до максимума (при имеющихся ресурсах) прибыль комбината. Современные ЭВМ способны отыскивать оптимальные планы при числе видов продукции до 1000 и числе ресурсов до 500 (не желая утомлять читателей, мы не будем подробно разъяснять, что эти виды продуктов необязательно должны быть строительными материалами и называться в честь великих математиков). Применение ЭВМ позволяет повышать прибыльность планов на 10-12%, не повышая количества ресурсов.

- Постойте, но почему в качестве единственного показателя плана вы приняли прибыль? Ведь есть еще вал, рентабельность, производительность труда, фондоотдача и много других показателей, которые характеризуют план.

Мы замялись... Со всеми предыдущими репликами нетерпеливого голоса удавалось небрежно расправляться с помощью убедительных аргументов, а тут... Первой мыслью было вычеркнуть "неудобный" вопрос, забыть его и продолжать восхваление методов оптимального планирования. Но вспомнив неосторожное обещание во введении и попеняв за него друг другу, мы все- таки попытались ответить.

К сожалению, целевая функция может быть только одна. И если кто-нибудь призывает вас добиваться максимальной прибыли при минимальном расходе ресурсов, максимальной рентабельности и минимальных трудозатратах, объясните ему, что он требует невозможного^*. Строго говоря, можно искать лишь наилучшее плановое решение по какому-то одному показателю, зафиксировав остальные. Например, как мы делали выше, искать максимум прибыли при заданных количествах ресурсов. Или стараться добиться минимума расхода ресурсов (в рублях) для достижения заданной прибыли. Но максимум прибыли при минимуме ресурсов - это нечто вроде сапог всмятку: минимальный расход ресурсов всегда равен нулю, хотя при нем и прибыль будет, естественно, нулевой. Однако жизнь есть жизнь, и она требует учета многих показателей. Как же с этим быть?

^* (Или предложите посмотреть, например, книгу И. Я. Бирмана "Оптимальное программирование". М., "Экономика", 1968)

В количестве предложений на этот счет недостатка нет, а проблема до сих пор окончательно не решена. Она тянет за собой слишком много других вопросов, решительно выходящих за рамки математики, ибо далеко не всегда можно сказать, что лучше, а что хуже. Эта неопределенность сказывается уже при решении вопроса, что именно следует строить. В самом деле, куда направить данный конкретный миллион рублей?

Это зависит от коллективного мнения членов общества. Скорее всего, мнения разделятся. Кто-нибудь один решит, что нужно строить квартиры, другой - трикотажную фабрику, третий будет горячо ратовать за производство сосисок со съедобной кожурой... Наконец, авторы знают одного члена общества, который непременно выскажется за то, чтобы на каждые три жилых дома приходился плавательный бассейн.

Еще хуже обстоит дело, когда приходится, оценивая план, выбирать между прибылью и трудоемкостью. Долгое время математики лишь смущенно пожимали плечами, когда к ним обращались с такими вопросами. Пожалуй, первым над ними серьезно задумался в начале нашего века экономист В. Парето. Суть предложения Парето можно представить себе так.

Если какое-то изменение плана улучшает некий показатель, но при этом ухудшает какой-то другой показатель, то планы не сопоставимы. Зато они становятся сопоставимыми, если все показатели одного плана лучше (или скорее не хуже) всех показателей другого плана. Так давайте считать оптимальным такой план, в котором нельзя улучшить ни один показатель, не ухудши при этом какого-то другого показателя. Скажем, найден план с прибылью 10 тыс. руб. и трудоемкостью 15 тыс. чел.-дн. И всякая попытка изменить этот план или снижает прибыль, или увеличивает трудоемкость. По Парето, такой план оптимален.

Но вскоре выяснилось, что почти в любой задаче планирования много оптимумов Парето, а вопрос о выборе между ними равнозначен решению первоначальной задачи, то есть дело не сдвигается с места.

Другое предложение сводится к тому, чтобы вырабатывать единый комплексный показатель К:

где П - прибыль, Т - трудозатраты и т. д., а k₁ и k₂ - весовые коэффициенты, показывающие относительную важность каждого показателя и уравнивающие размерности. Для отыскания этих весовых коэффициентов предлагается спрашивать сведущих людей, экспертов, отчего и сам метод носит название метода экспертных оценок. Об этом методе мы еще поговорим, когда речь будет идти о строительном проектировании.

Если экономистов можно упрекнуть в нечеткости при решении коренного вопроса о показателях качества планов, то в отсутствии фантазии их никак не упрекнешь. Какие только единые показатели не предлагались! Вплоть до максимума средней продолжительности жизни каждого члена общества^*. Говорят, что такой единый показатель не устроил медиков и мотоциклистов...

^* (Мы здесь имеем в виду печатные работы серьезных экономистов, а не вечерние беседы в студенческих общежитиях. (См. А. И. Каценелинбоген, Ю. В. Овсиенко, Е. Ю. Фаерман. Методологические вопросы оптимального планирования социалистической экономики. М., "Наука", 1966).)

Такие задачи, где ищется минимум некоторого показателя при наличии ограничений, называются сейчас задачами математического программирования^*. Если показатель и ограничения включают неизвестные плановые параметры лишь в первой степени, то это задача ЛП.

^* (Не путать с "программированием на ЭЦВМ", то есть с переводом алгоритмов на язык машин, о котором пройдет речь ниже. Вообще слово "программирование" оказалось сейчас на русском языке перегруженным содержанием. Положение еще больше запуталось, когда стали говорить и о "программированном обучении" как педагогическом приеме. Если читатель хочет никогда не теряться в этом вопросе, советуем в качестве упражнения разобраться в смысле выражений: "обучение математическому программированию", "программированное обучение математике", "обучение математиков программированию".)

Сложнее обстоит дело, если приходится планировать на длительный срок. Ведь прибыль, полученная сегодня, и прибыль, которую мы получим через пять лет,- это не одно и то же. Народная мудрость отдает предпочтение синице в руке. Но как быть, если альтернативой ей служит не журавль в небе, а, скажем, голубь на чердаке, которого можно поймать с большей вероятностью успеха? Для сравнения прибылей, получаемых сегодня и через пять лет, предлагается умножить их на коэффициент (1 + Е)^-5 Против этой формулы никто не возражает, но трудно договориться о значении ?: до самого последнего времени оно колебалось для разных областей народного хозяйства СССР в пределах от 0,08 до 0,4 (для строительства Е = 0,17). Теперь большинство согласилось с тем, что Е должно быть единым для всего Союза. Осталось решить, какое оно, а это не так просто.

Впрочем, отраслевые инструкции по планированию до сих пор содержат различные нормативные коэффициенты эффективности - их сторонники хотя и составляют меньшинство, но меньшинство воинственное. Да, впрочем, и Коперник был в свое время в меньшинстве...

Мы показали, как получается оптимальный годовой план. Удовлетворение ограничений по ресурсам гарантирует нам сбалансированность плана, а максимизация целевой функции - оптимальность. И смысл этой задачи следует постичь всем строителям.

Мы рассмотрели задачу оптимального годового планирования. Но планирование ведется на разные периоды.

Составляются самые общие двадцатилетние планы-прогнозы. Затем эти планы конкретизируются в виде пятилетних. В пятилетних планах масштаб таков, что многие мелкие детали ускользают. Например, если планируется производство сборного железобетона, то весь он в пятилетнем плане предстанет в одеянии безликих кубов (кубометров). Далее на стадии годового планирования происходит самое грубое деление железобетона на пять- шесть групп изделий - плиты, колонны, фермы и т. д.

Планирование поставок железобетона внутри кварталов (квартальное планирование) производится уже с большим числом групп. Но все же такое разделение недостаточно подробно, чтобы можно было в рамках месячного планирования разнарядить заводам сборного железобетона конкретные поставки определенных марок изделий на определенные объекты к определенному сроку. Конечный пункт такой детализации - марка изделия - рождается из кубов лишь на этапе месячного планирования. Прослеживается простая закономерность: чем ближе становится планируемый период, тем подробнее для него разрабатывается план. В самом деле, было неразумно вносить изменения в весь пятилетний план оттого, что понадобились изменения в текущем месяце: эти изменения скорее всего можно скомпенсировать всего лишь в рамках квартала.

От этих рассуждений один шаг до формулировки непременного свойства современного планирования - его непрерывности. Каждый новый план является конкретизацией плана более крупномасштабного и в то же время его корректировкой. Таким образом обеспечивается плавный переход от пятилетки к году, от года к кварталу, от квартала к месяцу, от месяца к декаде... Впрочем равномерный ли? Действительно ли при такой системе плавно уменьшается длина временного периода и удается без ущерба перейти к плану на более краткий период? В месяце три декады, в квартале три месяца, в году четыре квартала, в пятилетке... Стоп! Вот здесь как раз и намечается разрыв - слишком трудно шагнуть от пятилетки к одному году. Экономисты знают: труднее всего добиться сбалансированности планов именно по годам, по месяцам и декадам - проще. А отсюда простои, нехватки материалов, сбои в монтаже - весь набор неприятностей, который сулит строителям несбалансированный план. В самом деле, если, скажем, за пятилетку в целом предприятия стройиндустрии способны снабдить строителей железобетонными колоннами, то отсюда еще не следует, что те получат, все что хотели в третьем квартале второго года.

А нельзя ли ввести промежуточный этап планирования между пятилеткой и годом и тем самым заполнить неприятный пробел?.

Так родился Орловский эксперимент, двухлетка, которая способна обеспечить плавный переход на этом самом трудном стыке планов. Рождается двухлетка каждый год; первый год конкретизируется и уточняется на основе предыдущей двухлетки, а второй появляется заново каждый раз на основе пятилетнего плана. Стоит ли говорить, что реализация такого непрерывного планирования намного облегчается с помощью АСУС.