Оптимальное управление

Это высшая - форма всех режимов управления, в которой решения подчиняются требованию оптимальности в соответствии с какими-либо принятыми критериями. Именно такую форму управления и должны обеспечивать автоматизированные системы управления и проектирования в строительстве.

Действия Павла Ивановича, которые мы обсуждали выше, производились в режиме следящего управления, даже с элементами самообучения, так как он, несомненно, использовал свой богатый опыт строителя с тридцатилетним стажем. Но принятые им решения, как мы видели, далеки от оптимальных. К сожалению, это не есть особенность только данного руководителя: непонимание возможностей оптимального управления и незнание его методов характерны для многих строителей. Вот почему, в отличие от многих других книг по кибернетике, мы уделим в дальнейшем основное внимание именно оптимальному управлению. Мы покажем, какие выгоды сулит оптимальное управление и в области строительного производства и, что не менее важно, в области проектирования.

Заметим, что принцип оптимальности может быть заложен во все рассмотренные нами виды управления как в программном, так и в следящем режиме. Например, в программном режиме может быть составлено оптимальное расписание поставок бетона на объект, а в следящем режиме стремятся сократить простои. В то же время для обеспечения минимального отклонения от расписания поставок придется использовать комбинацию обоих режимов.

Границы между различными режимами управления могут быть размыты. Бывает и так, что одни параметры системы регулируются в программном режиме, другие - в следящем... Пример программного режима - это порядок ухода в отпуска, всякие нарушения которого обычно встречаются в штыки, или выдача зарплаты два раза в месяц. А вот, скажем, повышение в должности - это управляющее воздействие, которое иначе как в следящем режиме не осуществишь: нужно знать профессиональные качества работника и историю его деятельности. В целом можно утверждать, что управление системой тем лучше, чем большее число ее параметров переведено на принцип оптимального управления.

Для того чтобы управлять, нужно иметь информацию. Кое-кто до сих пор считает, что это необходимое условие является и достаточным, то есть что хорошее качество управления обеспечивается одной лишь хорошей организацией системы информации. Это привело к присвоению некоторым информационным системам почетного звания автоматизированных систем управления. Однако информация - это лишь сырье для производственного процесса управления, цель которого - выработка управляющих воздействий. И как нетрудно себе представить производство, заваленное сырьем, но тем не менее не справляющееся с планом, так и легко вообразить плохое управление при отлично поставленной информации.

Для тех, кто склонен преувеличивать значение информации, нелишне будет узнать, что существуют методы оптимального управления при неполной информации. Необходимость в таких приемах возникает в том случае, когда так или иначе требуется принять какое-либо решение, а недостающей информации ждать неоткуда.

Как можно принимать решения в условиях нехватки информации и что при этом теряется - поможет нам установить история, случившаяся с нашим знакомым по первому дню, старшим прорабом Солодковым.

...Настроение Солодкова было неважным: систематически подводил транспорт, план не выполнялся, ни в трест, ни в управление не дозвонишься. А каждое утро нужно было решать, сколько бригад направлять на отдаленный объект -'птицефабрику. Можно использовать эти бригады и на других объектах, но все равно была неясность насчет того, как они будут загружены.

Схватившись по привычке очередной раз за безмолвный телефон и чертыхнувшись про себя, Солодков обратился к лежащей перед ним таблице.

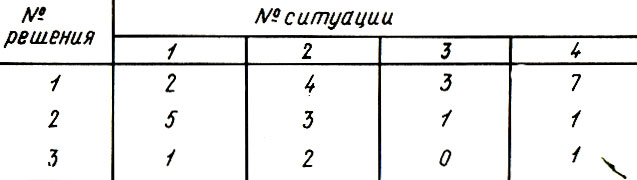
Выработка в тыс. руд. в зависимости от принятых решений

В распоряжении Солодкова были три разных решения. В зависимости от того, как будут обеспечены материалами и транспортом объекты, эти решения приводили к четырем различным выработкам, показанным в таблице. Какой будет выработка в каждой из ситуаций и для каждого из принятых решений - это Солодков знал. Но что из этого, если он все равно не знает, какая из ситуаций реализуется на самом деле. Какое же решение принять? Пока ясно только одно: решение 3 принимать не стоит, оно хуже других в любом случае. Какая бы ситуация ни возникла, выработка при решении 3 будет меньше, чем при двух других решениях. Но какое из двух оставшихся следует выбрать?

Ведь жизнь устроена по закону падающего бутерброда: в надежде на ситуацию 4 примешь решение 1 (выработка 7 тыс. руб.), а на поликлинику, как назло, не завезут раствор и будет простой (ситуация 1). С другой стороны, если понадеешься на ситуацию 1 и примешь решение 2, опять-таки может возникнуть ситуация 4. И тогда тысяча рублей - и все дела, хуже не придумаешь.

Но тут Солодков задумался. Встретилась ему вчера странная книжка под названием "Совершенный стратег", проглотил ее залпом перед сном, оторваться не мог^*. Так вот там предлагалось рассуждать так. Пусть в оптимальном случае принимается не одно какое-то решение 1 или 2, а попеременно оба решения, но в оптимальном соотношении. Первое в случаях, а второе - в р₂ случаях. И потребуем, чтобы гарантированная средняя прибыль была не меньше некоторой величины v, пока неизвестной.

^* (о-видимому, Солодков все-таки человек везучий: книжку Р. Вильямса "Совершенный стратег" (М., "Советское радио", 1962) уже давно днем с огнем не найдешь)

Рассмотрим при этих условиях первую ситуацию. Если бы первое решение использовалось во всех случаях, то выработка составила бы 2 тыс. руб. Но поскольку оно используется лишь в p₁ случаях, то средняя выработка составит 2 p₁ тыс. руб. В то же время выработка в результате принятия второго решения составит 5 р₂ тыс. руб. Общая выработка в первой ситуации равна сумме этих величин и должна быть не меньше v, то есть

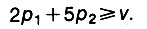
Это рассуждение можно повторить и для трех других ситуаций и получить

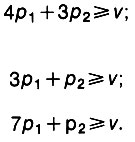
Кроме того, поскольку какое-то решение придется так или иначе принять, p₁ и р₂ в сумме должны равняться единице:

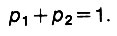
В этих условиях частоты использования решений р₁ и р₂ нужно принять таким образом, чтобы обеспечить максимальное значение средней выработки, то есть чтобы максимизировалась величина v. Задача отыскания p₁ и р₂ - это задача линейного программирования (см. четвертый день), и решать ее Солодков умел^*. Под нетерпеливое "гудение" бригадиров он решил задачу и получил р₁=⁴/₅, р₂ = ¹/₅. Гарантированная средняя выработка v при этом составила 2,6 тыс. руб. Значит, в четырех случаях из пяти нужно принимать решение 1, а в одном - решение 2. Но как реализовать такое странной смешанное решение? И тут произошло нечто совсем непонятное для обступивших Солодкова бригадиров: Солодков посмотрел на часы... и тогда разослал бригадиров по местам в соответствии с решением...1!

^* (А вы думали, все прорабы лыком шиты?)

А все объяснялось просто. Чтобы реализовать смешанную стратегию, как называется полученный Солодковым результат, ему нужно было разыграть случайную игру, в которой бы орел выпадал вчетверо чаще решки. Р. Вильямс рекомендовал такой способ: посмотреть на часы, где положение секундной стрелки близко к случайному. Если секундная стрелка окажется между 0 и 12 секундами, то нужно принять решение 2, если на остальных 4/5 циферблата, то решение 1. Секундная стрелка оказалась на 13 секундах, и Солодков принял первое решение.

К сожалению, такой образ действия небезупречен. Он более или менее оправдан лишь тогда, когда действиям руководителя противостоит спящий противник, который ему сознательно вредит. Но вряд ли кто-либо сознательно лишает стройки материалов. Поэтому принятая Солодковым стратегия носит перестраховочный характер.

А теперь прикинем, что приобрел бы Солодков, будь в его распоряжении, скажем, одна лишь вероятностная информация о могущих возникнуть ситуациях. Ну, например, сведения о том, что все ситуации равновероятны. Тогда вероятность каждой составила бы 0,25 и каждое из решений дало бы следующую выработку решение 1:

решение 2:

Ясно, что в этих условиях, приняв решение 1,

Солодков получил бы выработку 4,0 тыс. руб., что на 1,4 тыс. руб. больше средней выработки при отсутствии информации.

Этот несложный расчет иллюстрирует следующее общее положение: за отсутствие информации приходится платить. Но и сама информация обычно не достается бесплатно. Так что существует некоторый оптимальный уровень информированности руководителя, при котором его деятельность наиболее эффективна. Информация, поступающая сверх этого уровня, уже не будет окупаться качеством решений.

Ну скажем, если в нашем случае за информацию о вероятностях возникновения той или иной ситуации нужно заплатить 2 тыс. руб., то делать этого не стоит, лучше управлять в условиях неполной информации. Однако сейчас в большинстве случаев уровень информированности ниже оптимального, и его следует стараться повысить.

Итак, мы познакомились с частью проблем, которыми занимается кибернетика. А есть ли что-либо, чем она не занимается? Ответ прост: нет. Ибо если она еще чем-то не занималась, то лишь оттого, что не доходили руки.