Метод минимального элемента

Метод этот настолько прост, что угрозы не понять его для читателя не существует; гораздо реальнее угроза проникнуться навсегда неуважением к современным математическим методам. Основной принцип метода выражается фактически одной фразой:

на каждом шаге решения максимально возможная перевозка помещается на маршрут с минимальным тарифом (отсюда и название метода).

Поясним метод на примере. Самый малый тариф в клетке 1-4 (1 руб.). Хотелось бы провезти по этому маршруту как можно больше. Но сколько можно провезти? Первый завод может дать 100 м³ но четвертому объекту столько не нужно: ему хватит 30 м³. Значит, на этот маршрут можно поставить, самое большее, перевозку в 30 м³, соответственно убрав потребность четвертого объекта и уменьшив на 30 мощность первого завода.

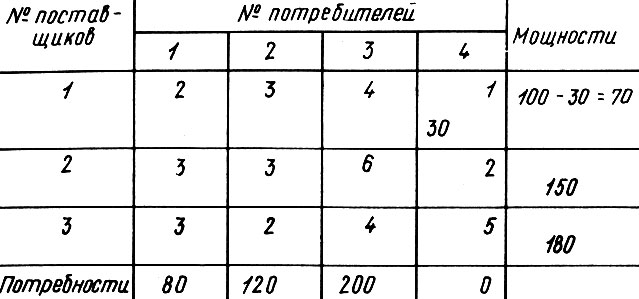
Теперь на последний столбец в таблице можно не обращать внимания и находить минимальный элемент в оставшейся части таблицы. Таких элементов два, и они равны 2 руб. В маршруты с минимальными тарифами можно внести перевозки соответственно 70 и 120 м³.

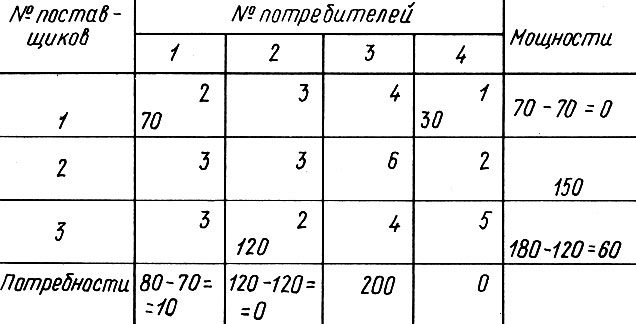
Теперь в таблице минимальный элемент равен 3 руб. и находится он тоже в двух разных клетках, но в одном столбце или строке. В таких случаях следует, вообще говоря, отдавать предпочтение тому маршруту, по которому можно больше провезти. Но здесь оба маршрута 2-1 и 3-1 допускают одну и ту же перевозку в 10 м³. Поэтому можно использовать любой из них. Наконец, уже без всякого выбора придется заполнить клетки 2-3 и 3-3, направив по этим маршрутам остаток груза. Получается следующая таблица (мощности и потребности нам не нужны).

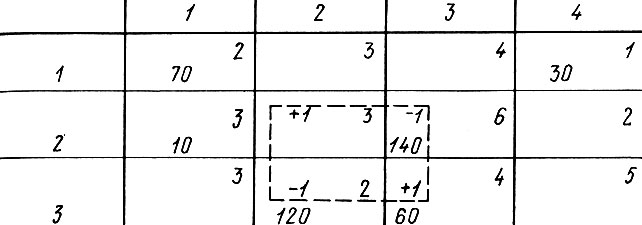
Стоимость перевозок Т по этому плану равна:

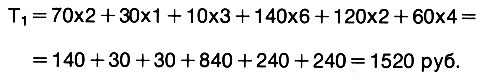
Казалось бы, мы рассуждали здраво, но не смогли избежать неприятного обстоятельства: на последнем шаге пришлось ставить перевозки на маршрут 2-3, не считаясь с тем, что тариф на этом маршруте велик. Это наводит на мысль, нельзя ли найти лучший план перевозок?

Мы рассмотрим самый простой, хотя и не самый эффективный метод улучшения допустимого плана, который носит название.