Распределительный метод

Обратим внимание на то, что одни маршруты мы используем (заполненные клетки), а другие нет (пустые клетки). Может быть, внеся перевозки в пустые клетки, мы сможем уменьшить транспортные расходы? Возьмем, например, маршрут 2-2, и поставим на этот маршрут 1 м³ груза. Это увеличит транспортные расходы на 3 руб. и вызовет следующую неприятность: нарушится баланс во второй строке и втором столбце. Попытаемся восстановить этот баланс, используя одни только заполненные клетки. Чтобы добиться баланса во втором столбце, снимем 1 м³ с маршрута 3-2, что уменьшит транспортные расходы на 2 руб., но нарушит баланс в третьей строке. Для восстановления баланса в третьей строке поставим 1 м³ на маршрут 3-3, что увеличит транспортные расходы на 4 руб. Наконец, снимая 1 м³ с маршрута 2-3, восстанавливаем баланс одновременно в третьем столбце и второй строке. Клетки, которых коснулись изменения, образуют при этом цикл. Подсчитаем полное изменение транспортных расходов Т при использовании маршрута 2-2 с перевозкой в 1 м³, которое назовем индексом клетки 2-2 и обозначим через

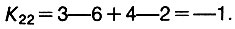
Значит маршрут 2-2 использовать выгодно, каждый кубометр груза, переданный на этот маршрут, позволит сэкономить 1 руб. Но коли так, то нужно постараться передать на этот маршрут как можно больше*! Беда, однако, в том, что столько же кубометров, сколько мы поставим на маршрут 2-2, придется снять с маршрутов 2-3 и 3-2, которые помечены в таблице знаком "минус". А с этих маршрутов можно снять всего лишь 120 м³: если снять больше, то перевозка на маршруте 3-2 станет отрицательной, что не имеет смысла - не повезем же мы бетон в обратном направлении^**. Произведем в клетках цикла указанные изменения, а остальные клетки оставим без изменений. Это приведет к следующему плану перевозок:

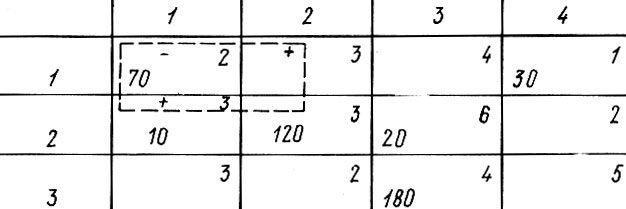
^* (Скажем, если бы мы сумели передать на этот маршрут 1520 м³, перевозки вообще стали бы бесплатными!)

^** (Тут читатель вправе упрекнуть нас в незнании жизни: перевозки материалов со строительных объектов обратно на заводы - это, увы, не столь уж редкое явление. Но вряд ли такие обратные перевозки могут привести к оптимальному плану)

Транспортные расходы по этому новому плану можно подсчитать таким же длинным путем, как и раньше, но можно и сократить этот путь. Действительно, если перенос на маршрут 2-2 одного кубометра уменьшал транспортные расходы на 1 руб., то перенос 120 м³ вызовет во столько же раз большее изменение. Иначе говоря, новые транспортные расходы представятся в виде

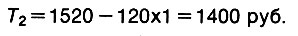
А мы перейдем к исследованию нового плана перевозок. Вычисляем индексы свободных клеток первой строки

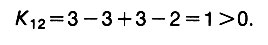
Это значит, что использовать маршрут 1-2 невыгодно.

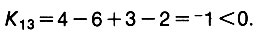
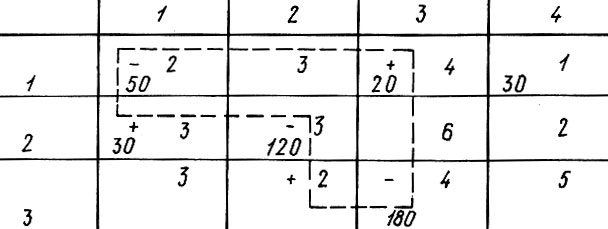
А вот маршрут 1-3 принесет уменьшение транспортных расходов, причем на него можно поставить 20 м³. И новый план перевозок примет вид

а новые транспортные расходы составят

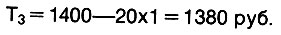
Отыскиваем новые индексы пустых клеток

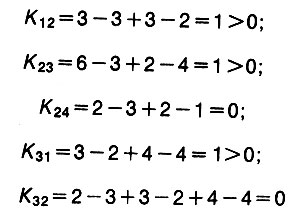
Обратим внимание, что для клетки 3-2 цикл состоит из шести клеток (он показан в таблице) - иначе передать в нее перевозку нельзя. Наконец, для клетки 3-4

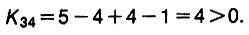
Итак, все индексы неотрицательны: значит, этот план перевозок улучшить невозможно. Первоначальный план перевозок нам удалось улучшить на 10%. В среднем планы перевозок удается улучшить на 7-8%.

Распределительный метод прост и удобен для ручного решения транспортных задач небольшого объема. Умение строить для них циклы достигается после решения вручную двух-трех задач. Для задач большого объема (с числом поставщиков и потребителей более 20) строить циклы сложнее, и на это уходит большая часть машинного времени. Поэтому были развиты методы, позволяющие сократить количество построений циклов (метод потенциалов) или вообще обойтись без них (венгерский метод).

Эти методы мы не будем здесь рассматривать, но лишь отметим, что современные ЭЦВМ позволяют решать транспортные задачи с числом потребителей и поставщиков до 500.

Разумеется, в рассмотренной задаче содержался ряд упрощений. Скажем, считалось, что стоимость перевозки прямо пропорциональна количеству груза (вот почему эта задача называется транспортной задачей ЛП), не учитывались специализация и другие факторы. Но даже в приведенном виде транспортная задача часто решается на практике и позволяет построить оптимальный план перевозок. Разумеется, жизнь так многообразна, что ее не втиснешь ни в какую математическую модель без существенной идеализации. Руководитель, которому машина посоветует оптимальный план перевозок, может и не принять ее совета в силу одной из тех причин, которые жизнь изобретательно выкладывает перед нами, нарушая самые лучшие планы. Скажем, на объекте 3 неожиданно заболел прораб, а его преемник толком не знает, куда укладывать бетон: ему вообще ничего посылать не стоит. Могут быть причины и более деликатные. Ну, например, водителя Задвижкина рискованно посылать на маршрут 4-4, ибо последний проходит в опасной близости от гастронома и возложит непосильную нагрузку на слабый характер мастера баранки. И только из-за одного этого летит оптимальный план. Таких примеров можно придумать много, но жизнь все равно еще изобретательнее, и с ее каверзами по плечу пока бороться только человеку - руководителю. Зато машина сильнее в так называемых хорошо формализованных задачах, например в обычной транспортной. Вот и получается, что человек и машина должны, не подменяя друг друга, делить бремя принятия важных решений. В машине человек должен видеть подспорье своему интеллекту.

Даже транспортная задача требует часто сильного усложнения постановки. Ну скажем, почему транспортные расходы должны линейно зависеть от объема перевозки? На самом деле при малых объемах перевозки это не так: за ста килограммами груза все равно нужно гонять трехтонный грузовик. И привезти их будет стоить немногим дешевле, чем полновесные три тонны груза. А при очень больших объемах перевозок может усилиться напряженность работы коммуникаций и снизиться скорость движения. Так что на самом деле зависимость стоимости перевозки Т от ее размера выглядит примерно вот так (рис. 11).

Рис. 11

Для многих видов грузов важен учет их партионности: некомлектные партии грузов вызывают не до груз.

Наконец, мы ничего пока еще не говорили о таком важном показателе, как коэффициент холостого пробега. Умелая диспетчеризация перевозок часто помогает гораздо рациональнее составить расписание ездок с учетом уменьшения коэффициента холостого пробега. К сожалению, для решения этой более сложной задачи не существует таких простых и логичных методов, как для транспортной задачи. И машина обычно способна дать лишь приближенное решение.

Даже в самой обычной транспортной задаче выливается в самостоятельную проблему определение тарифов. Для правильного определения тарифа нужно знать самый дешевый маршрут от поставщика к потребителю. Так возникает задача оптимальной маршрутизации.

Конечно, глядя на географическую карту, нетрудно прочертить по железным дорогам ближайший путь из Керчи в Вологду или из Вологды в Керчь. Несколько труднее будет найти скорейший путь, который не всегда совпадает с ближайшим: по некоторым дорогам ходят скорые поезда, по другим - только пассажирские. И уж куда сложнее становится эта задача, если ее предстоит решать машине, которая пока еще не может анализировать географическую карту. Для машины процесс выбора наилучшего маршрута должен быть формализован. И эта формализация достигается с помощью динамического программирования.

Начало нашей задачи вызывает в памяти картины далекого школьного детства: из пункта А в пункт Б движется самосвал с бетоном. На рис. 12 показана сетка дорог (не в масштабе), по которым может проехать самосвал, и пять возможных промежуточных пунктов. Требуется найти кратчайший путь.

Процесс решения задачи состоит из нескольких шагов. Сначала пронумеруем пункты в любом порядке, но желательно так, чтобы их последовательность хотя бы приблизительно отражала путь самосвала. Все вычисления сведем в таблицу.

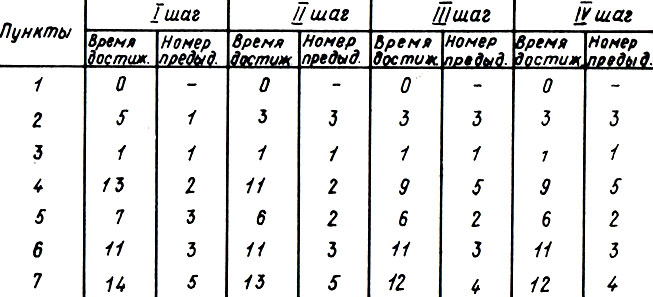
Проследим за тем, как заполнялась таблица. Пункт 1 достигается за нулевое время - это начальный пункт. В пункт 2 пока можно попасть только из пункта 1 за 5 мин. В пункт 3 можно попасть из пункта 1 за 1 мин (не забывайте фиксировать все это в таблице!). В пункт 4 можно попасть только из пункта 2, и займет это 5 + 8 = 13 мин. В пункт 5 можно попасть из пунктов 2, 3 и 4, и пути эти займут соответственно 5 + 3 = 8,1 + 6 = 7 и 13 + 3 = 16 мин. Разумеется, следует предпочесть путь из пункта 3, который займет всего 7 мин, что и отражено в таблице.

В пункт 6 можно попасть из пунктов 3 и 5 соответственно за 1 + 10 = 11 и 7 + 9 = 16 мин. Разумеется, путь из пункта 3 лучше. Наконец, в пункт 7 (или Б) можно попасть за 13 + 3 = 16, 7 + 7 = 14 и 11 + 5 = 16 дней, в зависимости от того, будем ли мы идти от пунктов 4, 5 или 6. Лучше всего идти из пункта 5. На этом оканчивается первый шаг вычислений.

Рис. 12

На втором шаге снова пройдем по порядку все пункты, обращая внимание на то, что время достижения каждого из них уже имеется. Так, уже в самом начале выясняется, что в пункт 2 можно попасть двумя путями: из 1 и из 3. В первом случае это займет 5 мин, а во втором (см. первый шаг) 1 + 2 = 3 мин. Занесем этот улучшенный результат в шаг II. Время достижения пункта 3 останется тем же, в то время как пункт 4 теперь удастся достичь за 3 + 8 = 11 дней. И так далее. Процесс оканчивается тогда, когда мы выясняем, что время достижения всех пунктов на двух соседних шагах не изменяется (для этого в данной задаче потребуется четыре шага).

Заметим, что, отыскивая минимум из продолжительностей пути от всех предыдущих пунктов, мы не интересуемся тем, как удалось попасть в каждый из этих пунктов, - это несущественно. Важен лишь результат во времени. Это и есть основной принцип динамического программирования, который, как мы убедимся, используется в самых разнообразных задачах.

Длины дуг, соединяющих пункты, могут выражать не только время движения, но и транспортные расходы - вот вам способ определения оптимальных тарифов.

Вот так или примерно так должна была бы реагировать АСУ на изменения в мощностях поставщиков бетона.

Транспортная задача интересна не только сама по себе. Она как кирпичики, из которых можно строить гораздо более сложные конструкции. Не будь ее, нельзя было бы и подступиться к задаче оптимального размещения производства, которая так важна в планировании. Читателю не составит труда разобраться с постановкой этой задачи, если он уже уверенно ориентируется в транспортной.

В самом деле, представим себе, что заводы сборного железо-бетона, которые должны снабжать наши стройки, еще не построены. Значит нам можно не заботиться о выполнении ограничений по мощности. Но в то же время не обойтись без дополнительных капвложений в эти заводы. Эффективность капвложений зависит от их объема и в то же время сказывается на себестоимости продукции. Таким образом, в целевой функций задачи придется учесть не только транспортные расходы, но и капвложения в строительство или расширение заводов, а также себестоимость производства на них.

Разумеется, задача размещения производства гораздо сложнее транспортной. А если читатель твердо уверен во всемогуществе современной науки, мы можем ему сообщить по секрету, что решать эту задачу точно до сих пор никто не умеет. Особенно большие трудности возникают тогда, когда заводы строятся по разным типовым проектам и мы не можем в силу этого как угодно дробить капвложения. А могучие современные ЭВМ? Они в лучшем случае позволяют найти приближенно оптимальное размещение производства. А что такое "приближенно оптимальное" решение? Чтобы ощутить это понятие, достаточно вспомнить, что приближенным значением числа а является любое число Ь.

...Ну а сейчас, на четвертый день, Павла Ивановича заботили уже совсем другие проблемы: снова горел план по яслям.

- К вам на прием математик, Скобкина, с утра сидит, - напомнила ему секретарша. - Жалуется, что работы по специальности для нее у нас нет.

- Кто? Математик? Зачем математик? Никаких математиков! У меня нет времени! Соедините меня, наконец, с Солодковым!