День 5. Календарное планирование (Кому, что, где и когда продавать?)

Открываем календарь, 
Начинается январь. 

С. Маршак

Этот день мы посвятим знакомству с календарным планированием. Для начала прислушаемся к разговору.

- Вызывали, Павел Иванович?

- Да, вызывал! Садитесь! Что же это, товарищ Солодков? Вы молодой, растущий инженер, а сетевые графики у вас не внедряются. Ну я еще понял бы...

Павел Иванович показал на стоящего у его стола начальника технического отдела Игнатия Евстафьевича, отличавшегося "здоровым" скептицизмом, но не закончил фразы.

- Есть трудности, - замялся Солодков.

- Не верю! Просто вы не освоили сетевое планирование! Или сейчас же докажите мне обратное!

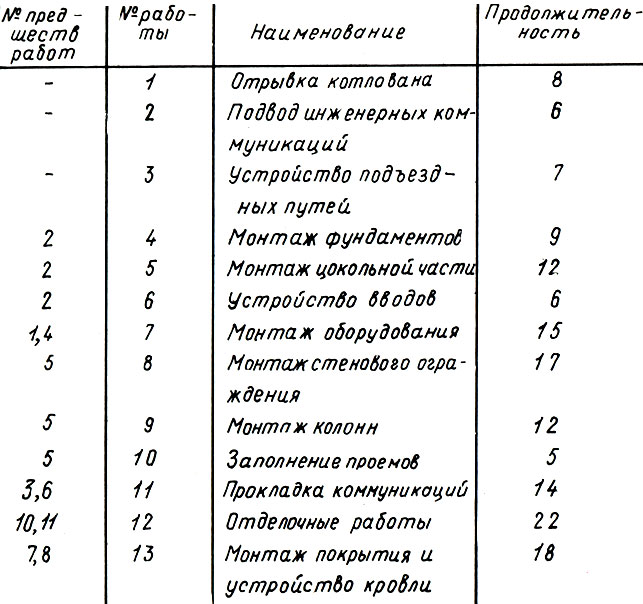
- Пожалуйста, - отчеканил самолюбивый Солодков и развернул бумажки. - Вот фрагмент сетевого графика для четвертого объекта. А здесь у меня перечень работ и какая какой из них должна предшествовать.

Здесь отражены связи между работами: например, монтаж стен не может начаться до окончания монтажа цокольной части и т. д. Для наглядного представления всех этих связей и для производства расчетов и служит сетевой график. Представим все работы в виде кружков с номерами, а стрелка между двумя кружками пусть показывает, что одна работа должна непременно предшествовать другой; вот так, скажем (рис. 13). Кружки, разумеется, можно расположить на бумаге и иначе, но стрелки будут иметь тот же смысл. В таком случае говорят, что сохраняется топология сети.

Последние два слова Солодков произнес с гордостью.

- А как рассчитать ранние и поздние сроки начала и окончания работы? - поинтересовался Павел Иванович.

- Сейчас. Пусть работы на объекте начинаются в нулевой день, а закончиться должны не позднее чем через 60 дней. Отразим на сетевом графике продолжительность каждой работы, ранний срок начала и поздний срок окончания, вот так (рис. 14). Тогда весь наш сетевой график будет выглядеть, если перенести из таблицы продолжительности работ, следующим образом (рис. 15). Ранние сроки начала первых трех работ, T₁, Т₂, Т₃, равны нулю (рис. 15). Работа 4 не может начаться до окончания работы 2; следовательно, ранний срок ее начала Т₄ равен 6, продолжительности работы 2. То же самое можно сказать о работах 5 и 6, которые также не могут начаться ранее чем через 6 дней. С работой 7 чуть сложнее: ей предшествуют две работы: 1 и 4. Работа 1 может закончиться, если ее начать в ранний срок, через 8 дней, а работа 4 - через 6 + 9 = 15 дней. Поскольку до начала работы 7 должны быть выполнены и 1 и 4, то ранний срок начала работы 7 Ту равен 15 дням. Точно так же для работы 11 ранний срок 7 начала равен максимуму из чисел 7 и 6 + 6 (ранний срок начала работы 6 плюс ее продолжительность, T^рн₆ + t₆), то есть 12 дням. С работами 8, 9 и 10 снова все просто: для них ранние сроки начал определяются ранним сроком начала работы 6 плюс продолжительность этой работы. То есть для всех трех работ они равны 18 дням. Наконец, для работы 13 ранний срок начала равен максимуму из 15 + 15 и 18 + 17, то есть 35, а для работы 12 - максимуму из 18 + 5 и 12 + 14, то есть 26. Ранний срок окончания последней работы называется критическим временем Т_кр . Чтобы его найти, нужно определить, какая из трех работ, 13, 9 и 12 кончится позже других: 35 + 18 = 53, 18 + 12 = 30, 26 + 12 = 38. Значит критическое время будет Т_кр =53 достигнуто на работе 13. Его определяет срок выполнения работы 8 - соединим эти две работы двойной линией. В свою очередь, выполнение работы 8 зависит от выполнения работы 5, а выполнение работы 5 - от работы 2. Эти четыре работы образуют критический путь на сетевом графике. Они отличаются от прочих работ тем, что задержка с их выполнением хотя бы в один день уже не позволит выполнить весь комплекс работ за 53 дня; за этими работами нужно следить особенно внимательно.

Рис. 13

Рис. 14

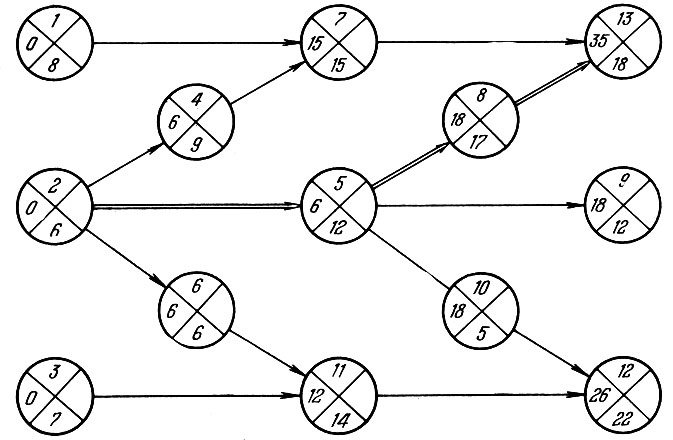
Рис. 15

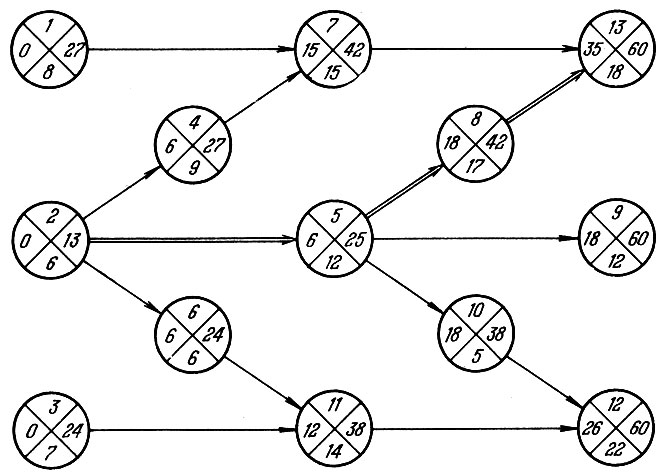
Рис. 16

Перейдем теперь к определению поздних сроков окончания работ. На весь комплекс нам выделено 60 дней (рис. 16). Следовательно, именно в этот срок должны завершиться последние работы комплекса 13,9 и 12, то есть Т^по₉ = Т^по₁₂ = Т^по₁₃ = 60. Чтобы весь комплекс завершился вовремя, работу 8 нужно закончить не позднее чем через 60 - 18 = 42 дня = Т^по₈ - иначе мы не успеем в оставшееся время выполнить работу 13. То же можно сказать и о работе 7. Работы 10 и 11 требуется окончить не позднее чем через 60 - 22 = 38 дней = Т^по₁₀ = Т^по₁₁. А вот с работой 5 дело обстоит посложнее: ее лимитируют поздние сроки окончания сразу трех работ - 8, 9 и 10. Соответственно поздний срок ее окончания 7?°будет равен минимальному из следующих поздних сроков: 42-17, 60-12 и 38-5, то есть 25. Так же определяются и прочие поздние сроки. Далее...

- Довольно, - прервал его Павел Иванович. - Вижу, что в сетевом планировании вы разбираетесь. Но тогда мне тем более неясно, почему вы его не внедряете.

- Сейчас объясню. На сетевом графике отражается только один вид зависимости между работами - полное предшествование, то есть какая из них не может начаться раньше окончания какой. На самом деле все гораздо сложнее. Например, работы 6 и 11 делает одна специализированная бригада, к тому же субподрядная. Это значит, что работы должны выполняться без перерыва - два раза они не могут приезжать.

- А разве это нельзя учесть? Да ведь можно вот так...

После нескольких попыток Павел Иванович вынужден был признать, что на сетевом графике это условие никак не отразишь.

- Затем, для работ по монтажу 4 и 7 нужен деся-титонный кран. Его мне только на 26 дней могут выделить.

- Это верно, он на другом объекте нужен.

- Не спорю. Но как это отразить на сетевом графике? Снова невозможно: как ни сделай, все будет не то. Наконец, работы 4 и 5, монтаж фундамента и цокольной части должны быть совмещены со сдвигом в 1 день. Даже работу 5 можно начать за 1 день до работы 4 - задел есть. Как мне это отразить?

- Вообще сетевое планирование - это эффективное техническое мероприятие, - сказал молчавший доселе Игнатий Евстафьевич и добавил: Для показухи пока. Для дела же - посмотреть еще надо.

Не по душе было Павлу Ивановичу это последнее замечание: начальник техотдела явно предпочитал работать по-старинке. Однако возразить нечего, ни ему, ни Солодкову: выходит, сетевой график, действительно, слишком грубый инструмент.

Выйдя из кабинета управляющего, Солодков с Игнатием Евстафьевичем честили на все лады сетевое планирование: было бы снабжение хорошее, да кадры, да транспорт не подводил бы... А потом ведь не все производственные ситуации удается учесть. Трудов сколько составить график, но чуть какое изменение - вноси исправления, а то и весь график на свалку. А без графика работать - в голове всего не удержишь. Где же выход?

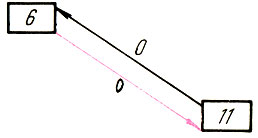
Рис. 17

Но тут в разговор вмешалась наша новая знакомая математик Ира Скобкина, которую заинтересовала возникшая проблема.

- Извините, пожалуйста, конечно без материалов и рабочих построить ничего нельзя, но календарное планирование поможет хотя бы лучше их использовать. А если обычная сетевая модель не может отразить взаимосвязи работ, попробуйте другие модели. Например, обобщенное сетевое планирование.

Маленькая рука уверенно взяла у него сетевой график и стала аккуратно исправлять.

- Разберемся в ваших затруднениях. Работы 6 и 11 должны выполняться непрерывно? Отлично! Соединим их двумя дугами нулевой продолжительности. Это и выразит требование, чтобы работа 11 начиналась не раньше окончания работы 6, но и, заметьте, не позже! То есть интервал между этими работами должен быть нулевым. Здесь удобно изображать работу прямоугольником, у которого левая сторона - начало, а правая - конец (рис. 17). На работы 4 и 7 отведено в сумме лишь 26 дней? Превосходно! Выразим это обстоятельство следующей дугой (рис. 18). Она показывает, что начало работы 4 и конец работы 7 не могут отстоять друг от друга более чем на 26 дней. Наконец, совмещенность со сдвигом работ 4 и 5 выразим следующим образом (рис. 19). Эти связи показывают, что работа 5 должна начаться не раньше, чем за 1 день до, и не позже чем через 1 день после начала работы 4, а закончиться может на 4 дня позже: ведь ее продолжительность больше на 3 дня, чем у работы 4. Измененный сетевой график примет такой вид (рис. 20).

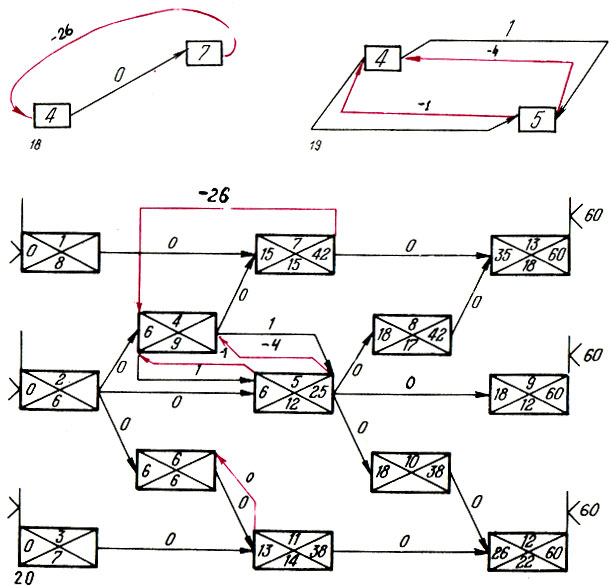
Рис. 20

- Но ведь в этом сетевом графике есть циклы, которые недопустимы: цикл показывает, что работа должна начаться раньше самой себя! Например, цикл между работами 4 и 7 (рис. 21).

- В том-то и особенность обобщенного сетевого графика, что циклы в нем допустимы. При этом только нужно следить, чтобы общая длина дуг и работ, вошедших в цикл, была не положительна. Так, для работ 4 и 7 длина цикла 9 + 15 -26 -2 < 0. Значит этот цикл допустим. Но теперь нужно скорректировать ранние и поздние сроки наступления событий - ведь они пока вычислены без учета отрицательных дуг. Для этого нарисуем часть графика, содержащую одни только отрицательные дуги (рис. 22). Этот график циклов не содержит. Числа, обведенные кружками, примем за исходные и посчитаем теперь по ним ранние начала и поздние окончания работ 4 и 6. В новом графике с одними только отрицательными дугами их можно считать как ранние и поздние сроки в обычном графике, но с учетом знака длины дуги. Так, для работы ^ ранний срок окончания есть

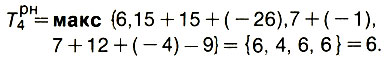
Для работы 6

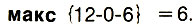
Теперь найдем поздние сроки окончания работ 7, 5,11. Для работы 7

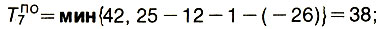
Для работы 5

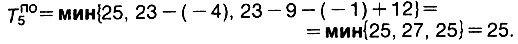
Внесем эти поправки.

В результате скорректировался лишь один поздний срок, но это требует повторного расчета по графику, не содержавшему отрицательных дуг. Для работы 1 поздний срок теперь станет

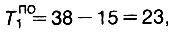
а для работы 4

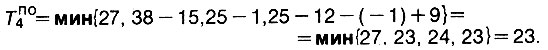
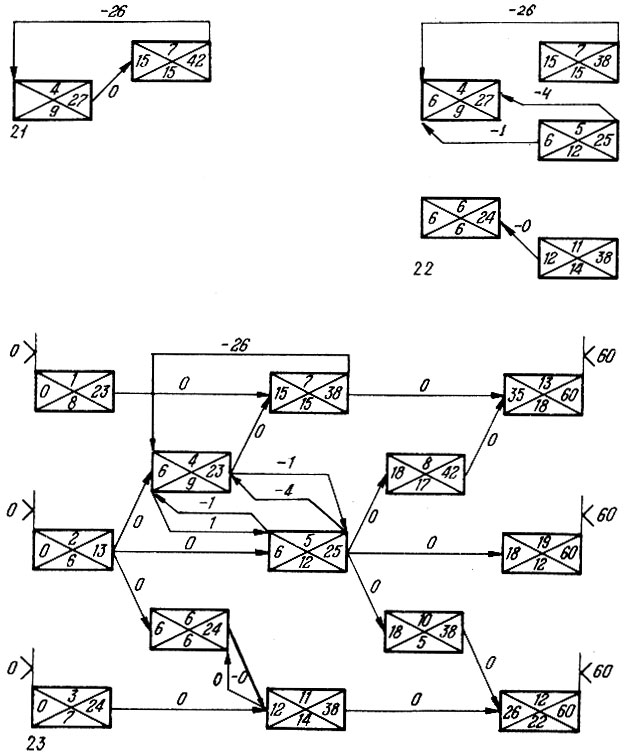
Рис. 21-23

Проведя расчет еще раз, можно убедиться, что ранние и поздние сроки не изменятся. Окончательно сетевой график с рассчитанными ранними и поздними сроками примет вид (рис. 23).

Как видите, в обобщенном сетевом графике сроки выполнения работ 1, 4 и 7 несколько сжались - это обычный результат учета дополнительных связей. На этом сетевом графике, как и на обычном, можно производить оптимальное перераспределение ресурсов.

- Интересная вещь! -сказал Солодков. - Но как нам ее внедрить? Может, вы поможете? Ведь вы у нас в тресте работаете!

- К сожалению, не могу. Я уже написала заявление об уходе, - ответили ему после небольшого раздумья.

...Конечно, приведенный выше сетевой график - это некоторый анахронизм. В современных автоматизированных системах управления нет нужды рисовать сетевые модели: по введенным исходным данным машина сама их формирует, производит необходимые расчеты и выдает сроки начала и окончания работ, резервы времени, расход ресурсов и прочие характеристики сетевого графика. Но приведенная модель дает представление о том, что при этом происходит в машине.

Надо признать, что обобщенные сетевые модели - это всего лишь ступень в совершенствовании календарного планирования строительного производства, причем одна из начальных ступеней. В этих моделях многие черты процесса строительства еще не учтены: вероятностный характер оценок продолжительности работ можно учесть в статистических сетевых моделях, многовариантность технологии и организации выполнения работ - в альтернативных моделях и т. д.^*

^* (Подробнее о различных сетевых моделях можно узнать, например, в "Основных положениях по разработке и применению систем сетевого плпнирования и управления", М., "Экономика", 1974)

Мы описали лишь расчет временных параметров сетевого графика при заданных продолжительностях работ. Но можно найти и оптимальные продолжительности, которые позволят, скажем, выполнить при заданных ресурсах все работы за кратчайшее время (временной критерий), с минимальной стоимостью (стоимостный критерий), или с наиболее равномерным использованием ресурсов (ресурсный критерий). Последний критерий чаще всего используется на практике: иной очень дешевый и быстрый, на первый взгляд, план выполнения работ приходится браковать, оттого что в нем первую неделю трудится 20 рабочих, вторую - 100, а третью - 10. Ясно, что для равномерной загрузки коллектива придется понизить интенсивность выполнения работ на второй неделе и растянуть их, скажем, на пару недель, зато в начале и конце следует поднажать.

Большие выгоды можно получить за счет определения рациональной очередности работ. Рассмотрим эти выгоды на примере работы двух бригад на ряде строительных объектов. Одна бригада отрывает котлован, другая - монтирует фундаменты. Последовательность работ той и другой бригады на объектах должна быть одинаковой, иначе возникнут слишком большие перерывы и придется дополнительно закреплять стенки котлованов от обрушения. Совмещение работ обеих бригад на одном объекте недопустимо с точки зрения техники безопасности. Пусть время работ каждой бригады в днях на каждом из 7 объектов задано в следующем виде:

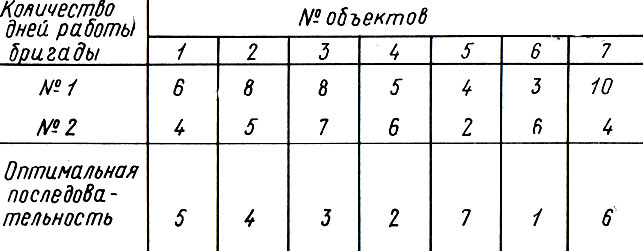
Допустим сначала, что мы, не задумываясь, приняли порядок выполнения работ на объектах, отвечающий их нумерации. Пока 1-я бригада будет трудиться на 1-м объекте, для второй фронта работ не будет. Через 6 дней 2-я бригада приступит к работе, но по истечении 4 дней она снова окажется без дела: для нее еще не будет готов фронт работ на втором объекте. И в дальнейшем из-за отсутствия фронта работ люди и техника нередко будут простаивать. Как же выбрать такую последовательность работ на объектах, чтобы все операции выполнялись за минимальное время?

Попробуем рассуждать. Из-за чего возникли первые простои? Очевидно, из-за того, что в принятой последовательности на первых двух местах оказались объекты первой бригады с большой продолжительностью работ. А отчего у 1-й бригады были простои в конце? Из-за того, что последние 4 дня работой обеспечена только вторая бригада, а первая уже все выполнила. Отсюда естественная перестановка объектов: объект с малой продолжительностью работы первой бригады должен ставиться в начале, а с малой продолжительностью работы второй бригады - в конце. Такая последовательность и указана в последней строке таблицы. Скажем, первым должен строиться шестой объект, вторым - четвертый и т. д. Заметим, что это несложное правило, которое носит название метода Джонсона, позволило нам уменьшить продолжительность работ на два дня.

Если число бригад больше двух и, тем паче, если возможно в некоторых пределах совмещать работы разных бригад, менять их последовательность, строгое математическое решение задачи становится не под силу даже современной ЭВМ. Вероятно, наиболее эффективными в этих случаях окажутся диалоговые методы: оператор сам задает машине вариант, скажем, с точностью до легко решаемой машиной задачи об оптимальной последовательности для двух бригад. Машина решает эти легко формализуемые задачи и выдает оператору конечный результат. Руководствуясь этими данными и своей интуицией, оператор вырабатывает новые варианты последовательности и оценивает их с помощью машины.

Таким образом, можно разыскать последовательность, наилучшую по "быстродействию". Впрочем, стоит ли всегда и любой ценой стремиться к сокращению продолжительности работ? Всякое решение оптимально лишь с точки зрения некоего принятого критерия, но может найтись иной разумный критерии (скажем, промежуточная готовность некоторой работы или надежность принятого плана), который укажет на изъяны принятого решения. А поскольку выбор критерия так или иначе акт субъективный, не следует переоценивать объективность полученных с помощью математики решений.

Кстати, о надежности. Применительно к несущим конструкциям о ней говорят уже давно. Но лишь недавно был поднят вопрос о надежности планов строительства. План должен быть не просто оптимален - он должен быть надежен. Иначе говоря, он не должен утрачивать силу в случае каких-либо непредвиденных, но не слишком серьезных обстоятельств. (Например, если весенний паводок начался на неделю раньше.) Конечно, и в обеспечении надежности нужна мера. Не следует, принимая решения, учитывать маловероятные случаи. Скажем, ни один разумный человек не станет учитывать возможность падения на место стройки крупного метеорита. Зато немало строительных планов, начиная с Вавилонской башни, оказались невыполненными из-за плохой взаимосвязи между звеньями. Жизненный опыт говорит о том, что между почти невероятным падением метеорита и вполне возможным ранним паводком помещаются тысячи больших и малых причин, могущих помешать стройке. Но строгий учет всех этих факторов разработан пока плохо.