Программа решения задачи о ханойской башне (пример использования рекурсивной процедуры)

В одной из древних легенд говорится следующее. "В храме Бенареса находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разного диаметра из чистого золота так, что наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это - башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя законам Брамы:

1) диски можно перемещать с одного стержня на другой только по одному;

2) нельзя класть больший диск на меньший.

Когда все 64 диска будут перенесены с одного стержня на другой, и башня, и храмы, и жрецы-брамины превратятся в прах и наступит конец света".

Эта древняя легенда породила задачу о Ханойской башне: переместить m дисков с одного из трех стержней на другой, соблюдая "законы Брамы".

Задача может быть решена одним перемещением только для одного (m = 1) диска, В общем случае потребуется 2^m-1 перемещений.

Назовем стержни левым (LEFT), средним (MIDDLE) и правым (RIGHT). Задача состоит в переносе m дисков с левого стержня на правый (рис. 17).

Рис. 17

Построим рекурсивное решение задачи, состоящее из трех этапов:

а) перенести башню, состоящую из (m - 1) диска, с левого стержня на средний (рис. 18):

Рис. 18

б) перенести один оставшийся диск с левого стержня на правый (рис. 19):

Рис. 19

в) перенести башню, состоящую из (m - 1) диска, со среднего стержня па правый (рис. 20):

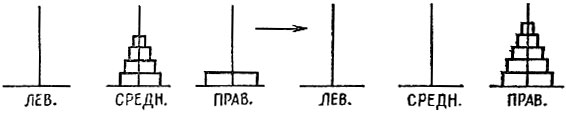
Рис. 20

Таким образом, задача о перемещении m дисков сводится к задаче о перемещении (m - 1) диска. Обращаясь опять к этому же алгоритму, сведем задачу к перемещению (m - 2) дисков. Продолжая этот процесс, получим в конце концов задачу о перемещении одного диска. Эта задача решается за один ход. Таким образом, в процессе решения возникают промежуточные задачи: переместить башню из нескольких (m) дисков с одного стержня на другой.

Обозначим тот стержень, с которого следует снять диски, через S₁, на который надеть - через S_k, а вспомогательный стержень через S_w.

Оформим алгоритм решения задачи о переносе башни из m дисков с S₁ на SR в виде процедуры MOVE с 4-мя параметрами: N, SI, SW, SK; алгоритм для п == 1 выделим в отдельную процедуру STEP, которая "перемещает" один диск со стержня S1 на SK.

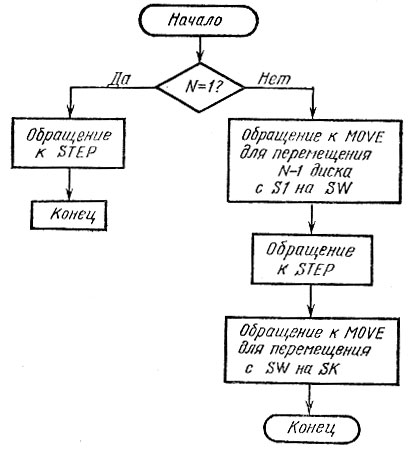
Рис. 21

Ниже приводится программа задачи о Ханойской башне и результат для перемещения 5 дисков.

Результат работы программы:

Итак, при решении поставленной задачи для пирамиды из пяти дисков необходимо произвести 31 перемещение. Это вселяет в нас оптимизм: жрецам придется долго трудиться, прежде чем "наступит конец света".