Интеллектуальные тесты на поиск аналогий [1980 Уинстон П.

Задачи поиска геометрических аналогий типа задачи, показанной на рис. 2.1, обычно присутствуют в интеллектуальных тестах для людей и представляют собой задачи, которые стандартно решались программой, написанной для вычислительной машины в 1963 году. Задача состоит в выборе правильной фигуры-ответа X, такой, что А так соотносится с В, как С соотносится с X, и такой, которая лучше всего при этом подходит. Иными словами, нам нужно правило, описывающее, как из С получается некое X, которое лучше всего соответствует правилу, описывающему, как из А получается В. Ключевым моментом при решении таких задач является хорошее описание таких правил. Когда такие описания имеются, работа над задачей сводится просто к вопросу поиска соответствия описании правил подобия. Поэтому оставляем себе состоящим из трех основных модулей, изображенных на рис. 2.2.

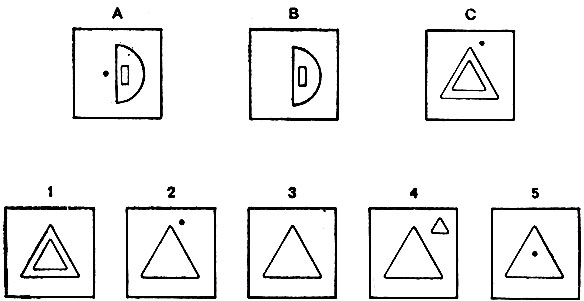
Рис. 2.1. Типичные входные данные для программы Эванса поиска геометрической аналогии

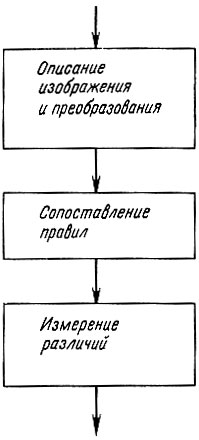
Рис. 2.2. Программа Званса состоит из трех важных модулей

Правила содержатся в таблице из трех частей

Наши правила описывают, каким образом одно изображение - исходное - становится другим - результирующим. Правила состоят из трех частей:

На рис. 2.3 показано типичное правило, предварительно преобразованное от вида, используемого в вычислительной машине, к виду, удобному для чтения. Обратим внимание на то, что метки l, m и n содержатся в обоих изображениях и в обоих описаниях. Размещение этих меток является результатом некоторой предварительной операции поиска соответствия, выделяющей подобные под изображения.

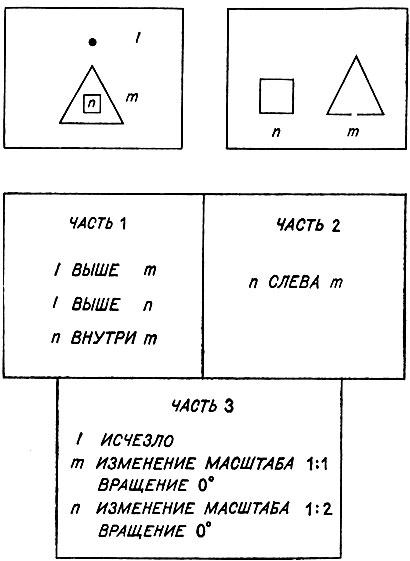
Рис. 2.3. Программа Эванса конструирует описания правил того, каким образом А становится В и как С может превратиться в каждый из возможных ответов. Эти правила состоят из трех частей. Две части описывают отношения между фигурами на изображениях, а одна описывает изменения отдельных фигур

Заметим также, что изменения во взаимоотношении частей изображения целиком заключены в описаниях исходного и результирующего изображения, т. е. в 1-й и 2-й частях нашего описания правила. Явным образом ничто не говорит о том, что переместилось изнутри m влево от него. В то же время изменения в отдельных под изображениях даются непосредственно и описаны в 3-й части описания. Вскоре мы увидим, каким образом эти три части участвуют в решении задачи, но сначала нам необходимо приобрести уверенность в том, что такие описания действительно можно вывести из рисунков.

Взаимоотношения частей изображения определяются просто

Ограничиваясь простой областью двумерных геометрических фигур, легко видеть, что при определении взаимоотношения между двумя фигурами никаких сложностей не возникает. Как показано на рис. 2.4, программа вычисляет расположение центров двух фигур, через центр одной из них проводит диагональные линии и отмечает, в каком из образованных при этом секторов содержится центр другой фигуры. Так как использованные отношения являются симметричными, то нет необходимости держать одновременно отношения слева и справа: отношение у СПРАВА-ОТ х излишне, если дано, что х СЛЕВА-ОТ у.

При решении вопроса о том, имеет ли место отношение ВНУТРИ в отличие от случая отношений ВЫШЕ и СЛЕВА, на первом шаге нужно убедиться, что фигуры не касаются друг друга. Тогда описывающая программа строит прямую, выходящую из любой точки внутри одной фигуры, ориентированную произвольным образом в направлении к границе рисунка, как показано на рис. 2.5. Если эта воображаемая прямая пересекает вторую фигуру нечетное число раз, то эта вторая фигура окружает первую. К счастью, в этом методе используются лишь формулы пересечения отрезков и он работает в случае произвольно сложных фигур.

Части 1 и 2 концентрируются на взаимоотношениях под изображений

Мы уже видели, каким образом взаимоотношения между фигурами изображения определяются в части 1 и части 2 каждого правила. Пример на рис. 2.6 подобран специально так, чтобы в рассмотрение вовлекались только часть 1 и часть 2. Часть 3 не участвует здесь потому, что при переходе от исходного изображения к результирующему под изображения не претерпевают никаких изменений.

Ясно, что наиболее подходящим является правило 3, так как если l ассоциировать с х, а m - с у, то совпадение будет полным. Заметим, однако, что заранее нет никаких причин в пользу того, чтобы ассоциировать l с х, а не с у. При переходе от исходного изображения к результирующему нам действительно необходимо, чтобы квадраты переходили в квадраты, окружности в окружности, треугольники в треугольники и т. д. Но эта потребность привести одну фигуру в соответствие с ей подобной не отражается при сравнении двух правил. В нашем примере в качестве ответа должно быть выбрано изображение 3, несмотря на то что под изображениями в А и В являются треугольник и квадрат, тогда как в С и во всех возможных ответах в качестве деталей изображения выступают окружность и точка. В общем случае при подборе правила программа подбора должна перепробовать все возможные пути ассоциации переменных друг с другом. В нашем примере у нас имеется две возможности:

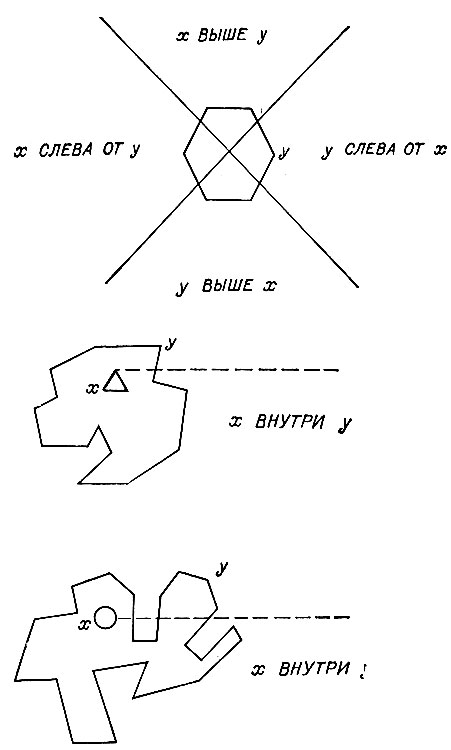
Рис. 2.4. Отношения между фигурами определяются путем вычисления их центров тяжести

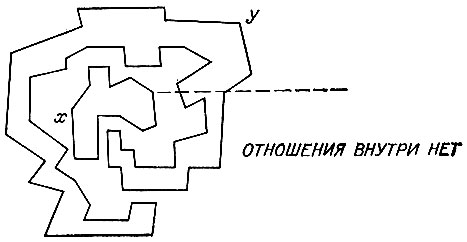
Рис. 2.5. Одна фигура лежит внутри другой, если неограниченный луч пересекает границы предполагаемой окружающей фигуры четное число раз

Из такой попарной ассоциации переменных вытекает, что число фигур на изображении, претерпевающих изменения, должно быть одним и тем же в обоих сопоставляемых правилах. Это же относится и к числу добавлений и стираний фигур. Всякая попытка сопоставить два правила, для которых эти числа различны, автоматически ведет к неудаче сопоставления. Это означает, что в задаче, показанной на рис. 2.7, изображение 3 получает преимущество по первоначальному соглашению, ибо правилу перехода от А к В может соответствовать только лишь правило, описывающее отношение между С и 3.

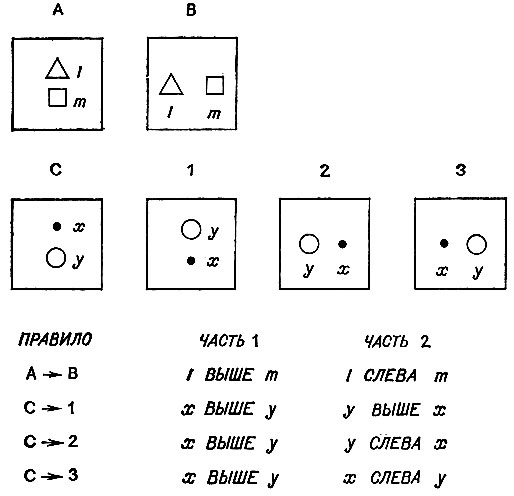
Рис. 2.6. К этой задаче имеют отношение лишь описания фигур на изображении, но не их изменения. Изучение правил показывает, что лучший ответ - это 3

Если в каждом из двух сравниваемых правил n фигур перемещается из исходного изображения в результирующее, то при поиске самого лучшего соответствия правил будет просмотрено всего n! способов ассоциирования переменных. В общем случае, если при переходе к результирующему изображению n₁ фигур (под- изображений) подверглось изменению, n₂ - добавилось и - исчезло, число возможных ассоциаций равно n₁!n₂!n₃!. Каждая из них должна быть испытана.

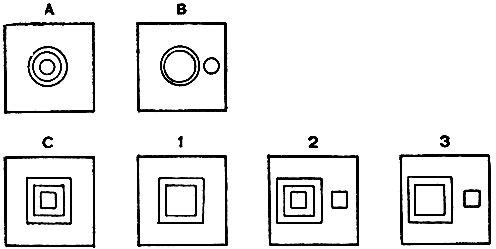
Рис. 2.7. Нельзя начинать приводить в соответствие переменные в правилах, если число фигур на изображении В и на изображении-ответе не одно и то же. По этой причине ответы 1 и 2 отклоняются и изображение 3 - единственно возможный ответ

Часть 3 правила связана с изменениями в под изображениях

Так как со стороны части 3 правил преобразования не допускалось никакого влияния, то мы имели возможность сосредоточиться на рассмотрении части 1 и части 2. Точно так же задача, представленная на рис. 2.8, позволяет сосредоточиться только на части 3. Поскольку на под изображениях не больше одной фигуры, то между под изображениями не может быть никакой связи и части 1 и 2 никак не могут сказаться на результате. Часть 3 немедленно ведет к решению, так как из всех подозреваемых фигур, лишь изображение 1 соответствует вращению на 45° без изменения масштаба.

Простой механизм придания веса правилам

Каким образом можно измерять схожесть двух правил? До сих пор задачи были настолько просты, что лучшее правило в точности соответствовало правилу перехода от А к В. Но если совершенного соответствия найти нельзя, то необходимо встроить некий механизм подсчета числа очков, даваемых правилами. Один из путей обеспечить это состоит в подсчете числа идентичных вхождений в двух правилах, т, е. в определении степени пересечения правил. Другая мысль состоит в определении того, как много следует выбросить из правила перехода от А к В для того, чтобы оставшаяся часть состояла только лишь из элементов, содержащихся в сопоставляемом с ним правиле. Интересно, что, как показывает чертеж на рис. 2.9, эти по-разному звучащие теории эквивалентны между собой. Поскольку величина окружности, представляющей элементы в описании правила преобразования от А к В фиксирована и остается одной и той же для всех сопоставлений правил, то нахождение правила, максимально пересекающегося с правилом преобразования от А к В, эквивалентно нахождению правила, которое минимизирует ту часть, которую следует выбросить из правила преобразования от А к В.

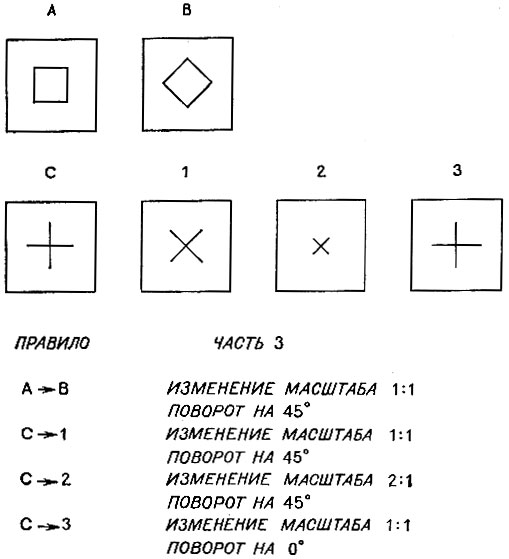
Рис. 2.8. Поскольку на каждом изображении имеется ровно одна фигура, то части 1 и 2 правил пусты. Изображение 1 правильно выбирается в качестве ответа с использованием лишь части 3 правил

Чтобы несколько настроить наш процесс, различные возможности, возникающие в части 3 правила, можно учитывать с меньшим весом, чем элементы частей 1 и 2. Если соответствие элементов в части 1 и 2 принять за единицу, то веса, подобные тем, что показаны на рис. 2.10, работают достаточно хорошо, если с этими коэффициентами добавлять элементы части 3 к общему весу сравниваемого правила. Совсем иное множество чисел могло бы быть результатом другого суждения о том, как следует упорядочить различные возможности. В данном множестве имеется тенденция пренебрегать отражениями, а какое-то другое могло бы дать предпочтение отражениям перед вращениями. Соответствующие программы при этом время от времени расходились бы в даваемых ими ответах.

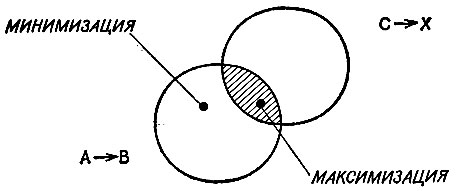
Рис. 2.9. Различия в правилах измеряются степенью их перекрытия. Ответы определяются путем поиска такого правила для перехода от С к X, которое имеет максимальное число общих элементов с правилом перехода от А к В. Точно к тому же результату ведет поиск правила перехода от С к X, при котором требуется меньше всего вычеркиваний из правила перехода от А к В

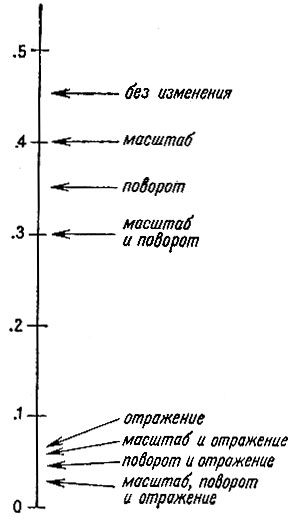
Рис. 2.10. Вклад от соответствия элементов в части 3 правила определяется используемым геометрическим преобразованием

Необходимо дальнейшее уточнение правила

Развитая до сих пор методика вполне годится для многих задач поиска аналогии, но в случае задачи, показанной на рис. 2.11, возникает трудность. При сравнении правила преобразования от А к В с правилом преобразования от С к 1 переменная х должна быть ассоциирована с l, а у - с y. Подобным же образом для преобразования от С к 2 необходимо противоположное сопоставление переменных. Но заметим, что при таких способах связывания переменных и преобразование от С к 1, и преобразование от С к 2 идеально соответствуют преобразованию А в В. Пока что у нас нет возможности отразить мысль о том, что при переходе от А к В и от С к 1 необходимо отбросить треугольник.

Трудность заключается в том, что никак не отмечается, соответствуют ли переменные, сопоставляемые в правилах, одной и той же фигуре или нет. Увеличивая несколько вес соответствий, в которых переменные относятся к подобным фигурам (под изображениям), можно решить нашу задачу. Хорошо работает добавка величиной 0.3 для каждой такой пары. В нашем конкретном примере общий вес преобразования от С к 1 увеличится на 0.3, вес преобразования от С к 2 не изменится. Благодаря этому изображение 1 будет выбрано в качестве наилучшего ответа.

Фигуры, соответствующие друг другу, могут оказаться не единственными

До сих пор предполагалось, что фигуры встречающиеся на исходном и результирующем изображении индивидуализированы и отличны между собой, так что не возникает трудности при описании правила, дающего преобразование. Но в случаях, подобных показанному на рис. 2.12, возникает неоднозначность. Какой из двух треугольников исчез? Ясно, что больший. Но может быть малый треугольник был стерт, а больший сжат?

На самом деле в отрыве от остальной части проблемы ни одна из теорий не может отдать предпочтение какой-либо возможности. Следовательно, должны быть построены два правила в соответствии с каждым из способов, которыми треугольники на исходном изображении могут быть идентифицированы с треугольниками на результирующем изображении. Таким образом, для каждой пары исходное - результирующее изображения может существовать много правил и для каждого из них может быть несколько путей, по которым оно сопоставляется с другим правилом. Действительно, в некоторых задачах в качестве кандидатов на высшую оценку может выступать до сорока или пятидесяти ассоциаций для таких парных правил.

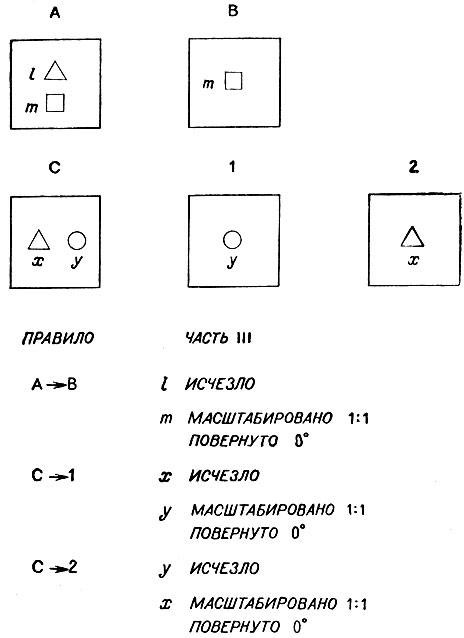
Рис. 2.11. При сопоставлении правил фигуры одного правила сравниваются с фигурами другого. Эти пары не обязательно состоят из геометрически подобных элементов, но если это так, то такому соответствию придается слегка больший вес. Для данной задачи два предполагаемых ответа равносильны без такой добавки. При ее наличии выигрывает изображение 1

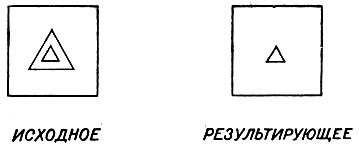
Рис. 2.12. Когда возникает более одного частного случая фигуры, вводятся варианты описания. Здесь можно было бы стереть большой треугольник, но, с другой стороны, можно было бы стереть малый, но при этом уменьшить размеры

Программа работает хорошо

Посмотрим на рис. 2.13. На нем показано несколько примеров, заимствованных из тестов, которые, очевидно, вполне доступны описываемой программе.

В первом примере 3 является верным ответом, и на самом деле 3 является единственным изображением, которое всерьез рассматривается программой, поскольку лишь только 3 среди всех изображений содержит то же число фигур, что и В. Напомним, что требование равенства числа фигур является неявным следствием того, что допускаются лишь сопоставления правил, в которых число добавлений, стираний и преобразований одно и то же.

Во втором примере наиболее разумным предположением относительно правила перехода от А к В является то, что стирается внутренняя фигура. Точно таким же будет правило для перехода от С к 3, и последнее изображение будет выбрано нашим процессом. Заметим, однако, что другим предположением о правиле перехода от А к В могло бы быть такое, когда внешняя фигура убрана, а внутренняя увеличена. При этом предположении верным ответом будет изображение 4. Но поскольку при подсчете веса описания, содержащие преобразования масштаба, оцениваются меньшим числом очков, чем преобразования, в которых нет никаких изменений, то будет выбран ответ 3, а изображение 4 будет вторым наиболее вероятным кандидатом. Ясно, что при отсутствии 3 изображение 4 будет первым.

В третьем примере правило перехода от А к В может быть описано либо как вращение, либо как отражение, причем 2 будет лучшим ответом, если в процессе отдается предпочтение вращениям, а изображение 1 - если предпочитаются отражения.

В четвертом примере при переходе от А к В урезается, по-видимому, центральная фигура. Однако программа такие случаи обрабатывать не может, поэтому, если она и добивается успеха, то благодаря какой-то иной точке зрения на задачу. Очевидным образом изображения 3, 4 и 5 сразу же исключаются из рассмотрения, поскольку они не располагают нужным числом фигур (под изображений). Могут подойти лишь 1 и 2. Правило перехода от С к 1 показывает, что обе фигуры переносятся из исходного изображения в результирующие и обе остаются неизменными. Однако в правиле для перехода от С к 2, видимо, происходит стирание окружности в центре и добавляется полукруг, так же как и в случае перехода от А к В. Таким образом, лучший ответ - это изображение 2. Его выбор объясняется дополнительными очками к весу, появляющимися, когда друг другу соответствуют два правила, в которых ассоциированные переменные соответствуют геометрически подобным фигурам.

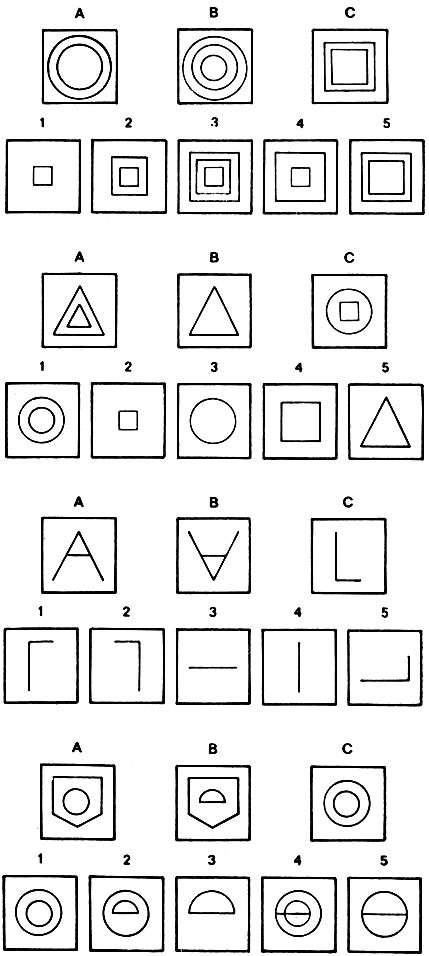
Рис. 2.13. Некоторые задачи, успешно решенные описываемой программой поиска геометрической аналогии

Процесс построения геометрических аналогий иллюстрирует ценность хороших описаний

Для процесса поиска геометрических аналогий, как и для многих других, можно дать несколько ответов на вопрос, что здесь наиболее важно:

Конкретные процессы следует изучать в деталях потому, что они демонстрируют общие принципы, или же потому, что они служат некими обобщенными метафорами, которые упрощают описание и понимание новых проблем. Это самоочевидно. Распространенный недостаток заключается, однако, в неумении выразить в нескольких словах, что же является важным. Попытки узнать, как что-то работает, не выяснив, почему это важно, обычно остаются бесплодными.