Обучение простым описаниям [1980 Уинстон П.

Наша следующая цель - сконцентрировать внимание на описании в контексте обучения, показав, что, располагая хорошим описанием, программа может обучаться на примерах, отобранных учителем.

На рис. 2.14 показаны частные случаи того, что мы, люди, считаем аркой (точнее говоря, показанная структура является горизонтальной перекладиной и парой опор, но для наших целей это не важно.). Заметьте, что серия начинается с типичной арки. На основании этого примера компьютер выводит очень общее представление о том, что есть арка,- он обучается тому, что арка - это два стоящих кирпича, которые являются опорой для третьего, лежащего на боку.

На это настраивается каждый последующий пример, уточняя некоторые обстоятельства. Во втором примере машине предъявляются те же объекты, но в ином расположении. Сказано, что элементы уже не образуют арки. Поскольку основное изменение состоит в том, что исчезло отношение опоры (поддержки), то машина делает вывод, что это отношение должно составлять важный аспект общего понятия арки. Заметим, что эта правильная мысль передается посредством одного тщательно подобранного примера, а не путем продолжительной статистической тренировки.

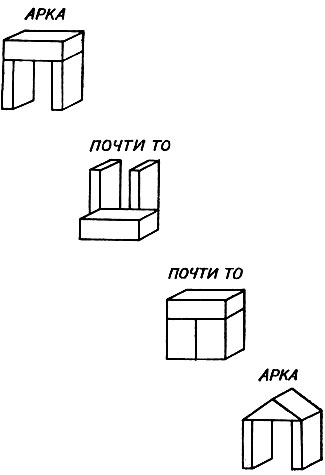
Рис. 2.14. Обучающая последовательность для понятия арки. Первый пример дает общее представление о ней. Другие подкрепляют его, подчеркивая необходимость поддержки, отсутствие касания опор и то, что сверху не обязательно должен быть параллелепипед

В третьем примере два стоящих кирпича соприкасаются. Снова машине говорится, что эта структура не представляет собой арки. Больше нет ничего такого, что сильно отличается от первой арки в нашей последовательности примеров. Очевидно, что в арке стоящие кирпичи не могут касаться друг друга. Снова прогресс был достигнут за счет хорошего примера и знания, что предъявленный образец - не арка.

Учитель в соответствии со своим вкусом может объявить четвертый пример аркой или нет. Если он дан как арка, то вычислительная машина отмечает, что не существенно, чтобы наверху находился именно кирпич. По меньшей мере, годится либо кирпич, либо призма. Естественно даже построить догадку, что приемлем любой параллелепипед.

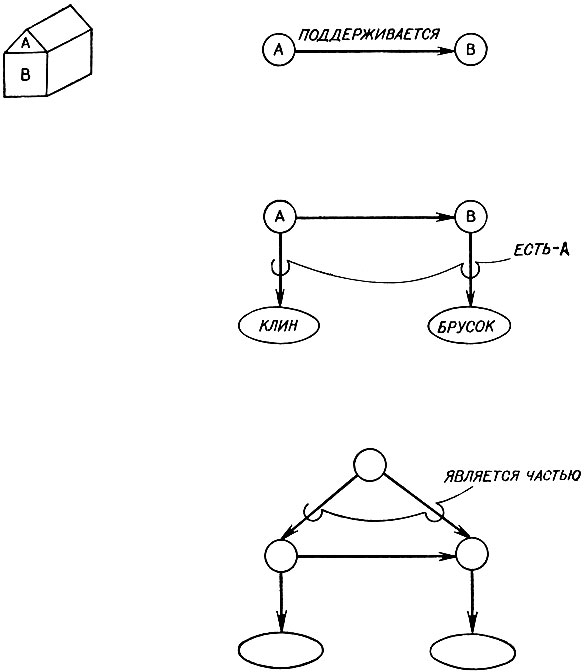
Рис. 2.15. Сцены могут быть представлены как сети связанных между собой понятий. В первой сети показано, что два таких узла-понятия связаны указателем ПОДДЕРЖИВАЕТСЯ. Во второй сети те же самые узлы связаны указателем типа ЕСТЬ с общими понятиями КЛИН и БРУСОК. В третьей сети указатели типа ЯВЛЯЕТСЯ ЧАСТЬЮ связывают вместе эти два узла, показывая, что они являются частью одного понятия, частного примера домика

Использование сетей приводит к лучшему описанию

Грубый сценарий далеко отстоит от тех точных деталей, которые требуются для создания работающей программы. Чтобы эта теория обучения работала, необходимо приложить значительные усилия в области представления знания. Простое неупорядоченное перечисление фактов, которое было вполне адекватным в задачах на геометрическую аналогию, здесь будет недостаточным. Мы его заменим схемой, с помощью которой знание записывается в ребрах и вершинах некоторой сети.

Предположим, на кирпиче лежит призма, образуя нечто вроде игрушечного домика, как на рис. 2.15. Эти предметы и вершины их представляющие помечены буквами А и В, так что соответствие очевидно. Оба предмета представлены вершинами. Тот факт, что А поддерживается В, отражен тем, что между этими двумя вершинами имеется указатель (стрелка) с пометкой.

В общем случае описание будет содержать как информацию об отдельных предметах, так и информацию о том, как они соотносятся друг с другом. Поэтому будут присутствовать указатели, подобные тем, что присутствуют во второй части рис. 2.15. Они указывают такие свойства, как принадлежность к определенному классу. Для наименования указателей можно было бы использовать терминологию теории множеств, но мы пользовались такими неформальными метками, как ЕСТЬ-А, поскольку они ближе к нормальному языку и более удобны в обращении.

До сих пор, конечно, единственное преимущество, которое мы получили по сравнению с прямым перечислением отношений, использованным в системе представления для задач о геометрической аналогии, состоит в том, что двумерный граф позволяет нам увидеть, каким образом отношения группируются. Теперь, однако, мы пойдем несколько дальше. В третьей части рис. 2.15 новые указатели отражают тот факт, что эти два предмета являются частями целого. Благодаря этому в нашем формализме появляется иерархическое группирование, которое совершенно отсутствует в программе на геометрическую аналогию.

Легко усвоить представление о домике

Уже сейчас мы располагаем достаточной описательной мощью чтобы понять на более глубоком уровне существующие программы обучения вычислительных машин. Рассмотрим, например, обучение понятию домика. Важно, чтобы присутствовали кирпич и призма, а также отношение поддержки между ними. Как машина может выучить эти факты?

Для начала учитель демонстрирует хороший типичный пример, на основании которого машина строит начальную, грубую модель в виде сетевого описания, как показано в первой части рис. 2.16.

Затем следующий пример, показанный во второй части рис. 2.16, обучает важности отношения поддержки. Этот пример не является домиком, но, поскольку он отличается от домика совсем немного, он будет называться "почти то".

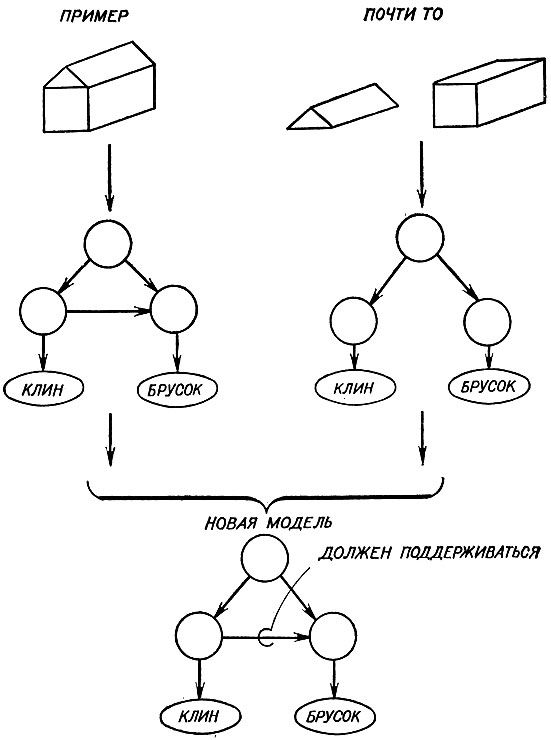
Рис, 2.16. Предъявление частного примера понятия всегда представляет собой необходимый первый шаг при обучении этому понятию. Здесь за примером домика следует 'почти то', в котором отсутствует отношение поддержки

На самом деле наше описание "почти того" отличается от исходного описания домика лишь одной деталью: отсутствует указатель ПОДДЕРЖИВАЕТСЯ.

Сравнение этих двух описаний естественно ведет к заключению, что указатель ПОДДЕРЖИВАЕТСЯ существен для домика. Таким образом, результатом синтеза двух описаний является новая, усовершенствованная модель, в которой указатель ПОДДЕРЖИВАЕТСЯ заменяется на его эмфатическую форму, а именно ДОЛЖЕН ПОДДЕРЖИВАТЬСЯ. Впредь ни одна из конфигураций не будет воспринята как домик, если нет указателя ПОДДЕРЖИВАЕТСЯ.

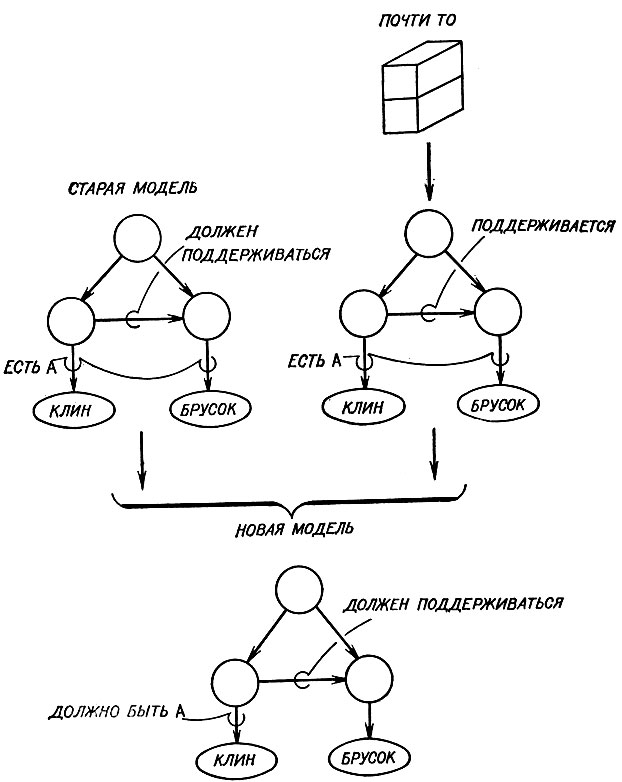
Рис. 2.17. Усвоение того факта, что на верху домика должен находиться клин, достигается путем демонстрации 'почти того', в котором наверху лежит другой предмет

Точно так же легко дать примеры "почти того", чтобы превратить указатели ЯВЛЯЕТСЯ в ДОЛЖЕН БЫТЬ. Сравнение описания кирпича, расположенного на кирпиче из рис. 2.17, с моделью, построенной к настоящему моменту, выполняет такую работу для верхней части домика. Отсюда легко выбрать следующие примеры "почти того", чтобы придать всем указателям желаемую эмфатическую форму.

Описание и примеры "почти того" - это существенные моменты

Необходимо выделить два фундаментальных обстоятельства:

Усвоив эти соображения, мы лучше поймем, как работает наша теория обучения в более сложных случаях.

При обучении понятию арки требуется более сложная система работы с различиями

Может случиться так, что пример будет отличаться от рассматриваемой модели в двух весьма схожих обстоятельствах. Это имеет место при обучении арке. Обратимся еще раз к последовательности обучения арке, чтобы увидеть, как наши представления работают на уровне различий между сетевыми описаниями.

Уже в самом начальном примере и первом же случае "почти того", показанных на рис. 2.18, имеется два различия, причем и там, и там отсутствует указатель ПОДДЕРЖИВАЕТСЯ. Разумной реакцией на это было бы предположить, что учитель преднамеренно ввел эти два различия и предполагает, что оба они будут рассматриваться одновременно и аналогичным способом. Поэтому оба отношения ПОДДЕРЖИВАЕТСЯ заменяются на ДОЛЖЕН ПОДДЕРЖИВАТЬСЯ на основании этого одного примера.

В следующем примере "почти того", показанном на рис. 2.18, точно так же возникает два различия одного сорта, а именно два новых указателя СОПРИКАСАЮТСЯ связывают между собой опоры. Теперь "почти то" отличается от арки не потому, что указатели отсутствуют, а потому, что добавлены лишние. Наверное эти новые указатели следует запретить. Это делается путем введения отрицательного НЕ ДОЛЖНЫ СОПРИКАСАТЬСЯ.

До сих пор "почти то" давал нам ограничения, демонстрируя предметы, не являющиеся аркой. По-иному работают положительные примеры. Рассмотрим окончательную конфигурацию, в которой наверху расположена призма. Если это арка, тогда определенное изменение в нашей модели должно отражать ослабление ограничения. По меньшей мере связка ЯВЛЯЕТСЯ между верхом арки и КИРПИЧ должна быть отброшена и заменена указателем ЯВЛЯЕТСЯ, ведущим к более общему классу, как показано на рис. 2.19. Переход к ПРОСТОЙ ПРАВИЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД представляет собой некоторую консервативную позицию по отношению к тому, насколько далекая индукция допустима на единственном примере. На рис. 2.19 показано, что существует цепочка все более общих понятий, связанных с КИРПИЧ и ПРИЗМА, ведущая к универсальной категории ВЕЩЬ. Новым направлением для указателя ЯВЛЯЕТСЯ может быть что угодно, расположенное в цепи отношений вида ОТНОСИТСЯ К КЛАССУ, в зависимости от того, насколько быстродействующей должна быть наша программа.

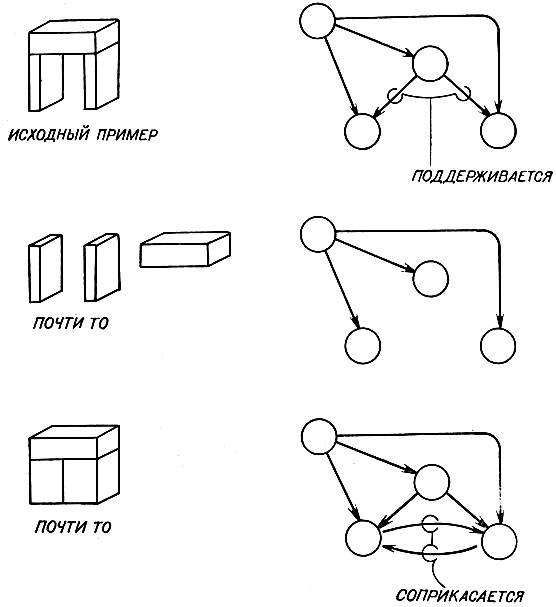
Рис. 2.18. Обучение понятию арки начинается с предъявления примера арки, дающего общее представление. Первое 'почти то' выделяет важность отношения поддержки. Далее 'почти то' с касающимися опорами показывает, что эти опоры не должны касаться друг друга. В обоих случаях 'почти то' используются два различия одного типа, которые обрабатываются вместе

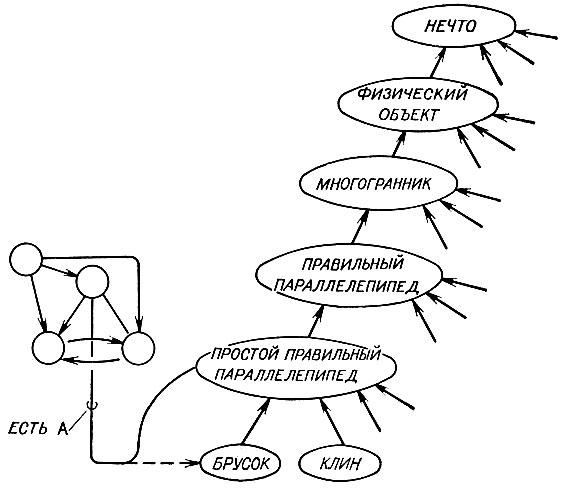
Рис. 2.19. Пример с заменой верхнего бруска клином способствует развитию более общей модели.. Степень обобщения зависит от того, насколько далеко пойдет процедура по цепи ЯВЛЯЕТСЯ

Имеется лишь несколько типов основных различий

Различия между описаниями направляют процесс обучения. Еще один проход по нашей системе поможет вскрыть ряд других подробностей. Рассмотрим два простых фрагмента сетей на рис. 2.20. Цель состоит в том, чтобы описать различия между ними. Во-первых, необходимо их сопоставить, решив, каким образом узлы одной сети соответствуют узлам другой. Как только это достигнуто, как только программа сопоставления достигла успеха в связывании друг с другом пар узлов, можно начать описание различий с создания некоторой скелетной основы, которая отражает общую структуру, содержащуюся в обеих сетях.

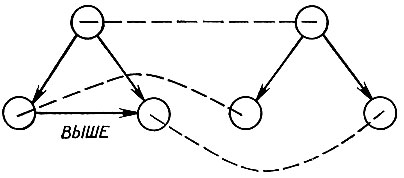
Рис. 2.20. Построение символических описаний представляет собой первый шаг обучения на примерах. Затем описание каждого примера сопоставляется с моделью, чтобы выделить сходство и различия. В процессе такого сопоставления делается попытка попарно связать узлы в этих двух сетях

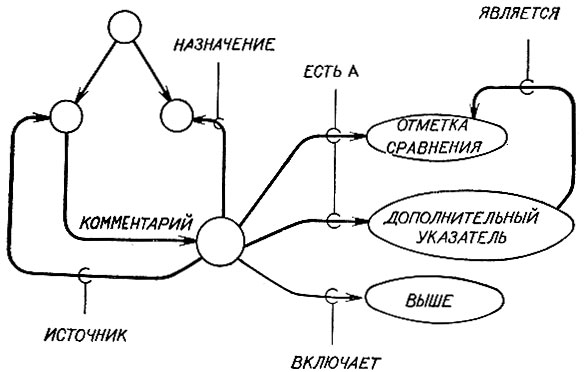
Рис. 2.21. Успешное сопоставление приводит к двойному результату: центральный скелет отражает то, насколько схожи эти две сети, а совокупность отметок о различиях сообщает о том, насколько они различны

Далее, отдельные различия характеризуются теми комментариями, которые приводятся на этом скелете. Один из таких комментариев гласит, что в одной сети есть такое отношение, которое отсутствует в другой. Эта отметка о различии имеет (и это достаточно удобно) ту же форму, что и другие узлы сети. На рис. 2.21 изображен скелет и отметка о различии.

Разнообразные отметки свешиваются с этой скелетной основы, как гроздья винограда. Полезно иметь несколько их типов. Те, что определены и проиллюстрированы на рис. 2.22, представляются удобными. Как отметки СОПУТСТВУЮЩАЯ ПАРА, так и отметки ВЗАИМОДОПОЛНИТЕЛЬНЫЙ УКАЗАТЕЛЬ имеют дело с отношениями между узлами, связанными в этих двух сопоставленных сетях. Можно было бы, конечно, отметку СОПУТСТВУЮЩАЯ ПАРА заменить двумя отдельными связками ДОПОЛНИТЕЛЬНЫЙ УКАЗАТЕЛЬ, но в общем случае целесообразно явно выделить тесно связанный характер таких пар. Другие типы различий связаны с отношениями, говорящими о том, как связанные узлы взаимо-относятся с остальной частью графа.

Различия вида СЛИЯНИЕ И ПЕРЕСЕЧЕНИЕ говорят на самом деле больше о сходстве, чем о различии. ВЫХОД же, однако, представляет собой истинное различие, состоящее в том, что от одной из сетей отходит стрелка-указатель, а от другой - нет. Конечно, конкретные указатели, появляющиеся в примерах различий, являются всего лишь представителями, и нет никаких ограничений на то, какими они могли бы быть.

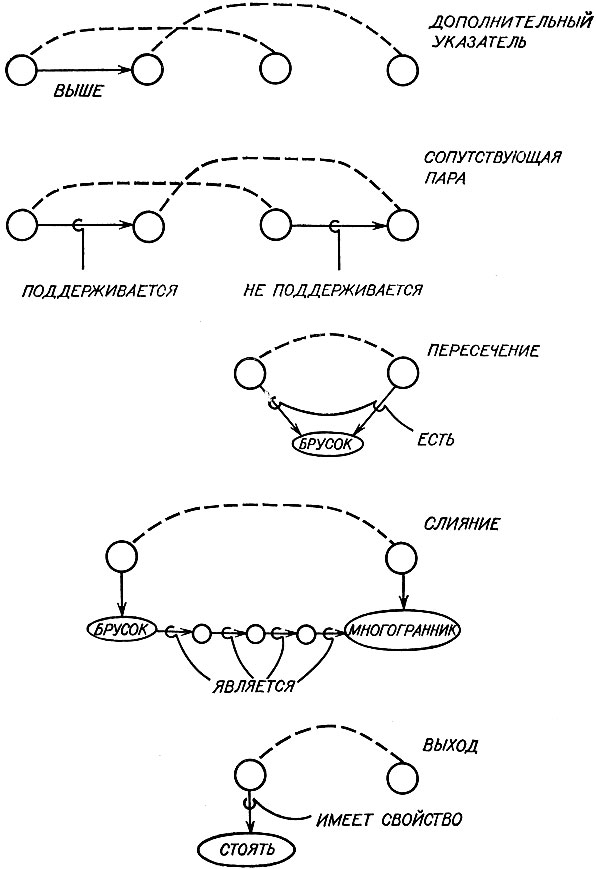
Рис .22 Возможны многие типы различий и подобий, некоторые из них показаны здесь

Теперь можно более четко сформулировать некоторые важные аспекты описания и процесса обучения:

На рис. 2.23 представлена таблица различий и реакций на них. Таблица невелика. Заметим, что некоторым различиям может быть дана не единственная интерпретация. Когда попадается такое различие, то действительной всегда предполагается первая интерпретация, до тех пор пока впоследствии некоторая новая информация не заставит ее пересмотреть.

Описание различия может включать общий комментарий

Хотя введенная техника описания уже достаточна для многих целей, обычно хорошо иметь некоторую возможность для помещения общего комментария, относящегося к наблюдаемым различиям. Возможно, что наблюдаются только отметки типа ПЕРЕСЕЧЕНИЕ или, быть может, отметки типа ПЕРЕСЕЧЕНИЕ и симметрия, наводящая на мысль об отметках СОПУТСТВУЮЩАЯ ПАРА, которые включают указатели ЛЕВЫЙ и ПРАВЫЙ. Такие наблюдения включаются непосредственно. Скелет с отметками различий становится лишь половиной описания, поскольку он дополняется структурой, дающей более непосредственный и организованный доступ к различиям. Как показано на рис. 2.24, к отдельным отметкам различий можно подойти либо через скелет, либо через комментарий о различиях. Благодаря этому создается явная организация описания различий, то, чего нет в программе на поиск геометрической аналогии.

Распознавание может быть осуществлено несколькими путями

Распознавание является подспудной целью обучения. Если обучение считается успешным, то из него следует более эффективное распознавание. Эффективность может потребоваться в нескольких, различных до некоторой степени направлениях. Вот два особенно простых примера:

Рис. 2.23. Каждое возможное различие соответствует некоторому специфическому действию, совершаемому над моделью. Если это пример 'почти того', предположительно играет роль лишь одно различие и предпринимается лишь одно действие, Если в выборке находится действительный пример, то над каждым наблюдаемым различием предпринимается действие

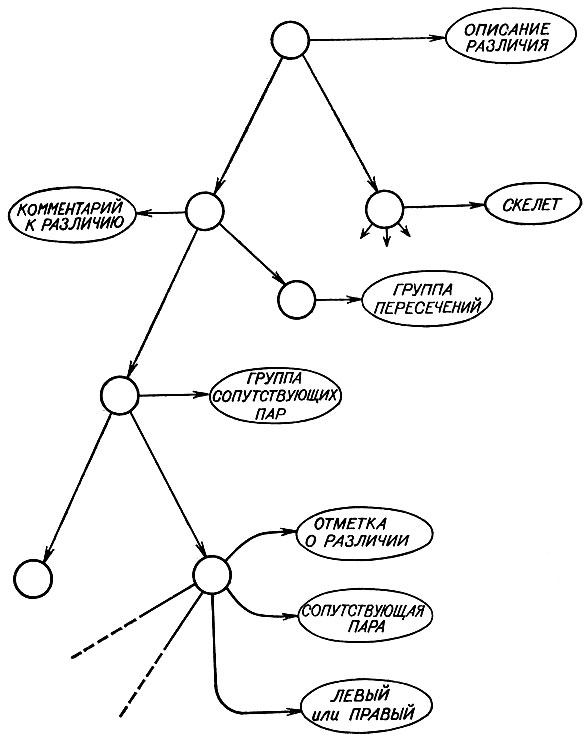
Рис. 2.24. Комментарий о различиях усиливает описание различий потому, что внимание непосредственно фокусируется на различиях, минуя скелет

Для первого приближения к удовлетворительному соответствию сосредотачиваются на обработке тех эмфатических отношений, которые обнаружены в модели. Ясно, что любые указатели с именами, начинающимися с ДОЛЖНО БЫТЬ, сообщают о тех позициях, где важность некоторого отношения была установлена в результате процесса обучения. Если на опознаваемом объекте отсутствует соответствующий указатель, то модель отклоняется без дальнейшего рассмотрения. Аналогично указатели модели, предваряемые НЕ ДОЛЖНО БЫТЬ, говорят об отсутствии соответствия, если опознаваемый объект имеет то свойство, о котором идет речь в указателе.

Если этим не ограничиваться, то для того, чтобы найти модель с наилучшим соответствием, а не просто первое же удовлетворительное соответствие, требуется оценка степени различия между опознаваемым объектом и каждой моделью. Необходимо перевести абстрактное понятие различия d ((опознаваемый объект), (модель)) в некоторую конкретную схему. Один из простых способов - подсчитать число различий.

Если эта мера оказывается слишком грубой, то можно сделать так, чтобы каждый тип различия оказывал регулируемое влияние на результат путем использования коэффициентов, отражающих важность различия данного типа:

Дальнейшее усовершенствование приводит к мере, чувствительной к тому уровню, на котором найдено различие, и к именам участвующих в нем указателей. Следует, однако, заметить, что такая аддитивная взвешивающая схема для совместного учета различных показателей является ограниченной. Во-первых, вся информация при этом сжимается в одно маловыразительное число. Это годится до тех пор, пока не возникает потребность понять, что будет дальше. Если распознавание путем выбора модели является конечной целью, то такой подход не приносит особого вреда.

Студент и учитель выполняют работу вместе

Каким образом обучение путем ознакомления с примерами структур из блоков вписывается в общую теорию обучения? Является ли оно изолированным, косвенно относящимся сюда феноменом, или же оно является чем-то позволяющим проникнуть в сущность центральных вопросов? Мы обязаны выкарабкаться из области исследования деталей и обратиться непосредственно к рассмотрению таких вопросов. В конечном счете наша цель - это изучение общих принципов интеллекта. Понимание конкретных систем полезно главным образом лишь как средство достижения этой цели.

Рассмотрим рис. 2.25. Здесь иллюстрируется точка зрения, согласно которой ничто не отбрасывается по мере движения вверх по иерархии типов обучения. На каждом шаге что-то добавляется к уже имеющемуся механизму. Обучение путем объяснения проще,чем обучение по последовательности примеров, поскольку нет необходимости решать вопрос о том, какие различия существенны и как ими пользоваться. Но на обоих уровнях необходимо располагать структурой данных, с помощью которой можно было бы усваивать информацию о том, что является важным. При обучении путем объяснения необходимо приводить описания, которые характеризуют сказанное, в соответствии с имеющейся к этому времени моделью, чтобы решить, где внести изменение.

Рис. 2.25. Обучение путем наблюдения примеров - это только один вид обучения. При переходе от более простых видов к более сложным часть нагрузки перекладывается с учителя на ученика, без изменения полного объема необходимой обработки

Таким образом, мы видим, что даже ниже уровня обучения по примерам необходимо иметь знакомые нам механизмы. Размышление о движении в другом направлении показывает, что эти механизмы сохраняются. Обучение путем открытия требует всех тех способностей, которые необходимы при обучении по примерам, а также дополнительно требуют, чтобы некоторый новый механизм взял на себя тяжелую задачу по генерированию примеров "почти того".

По мере перехода к высшим уровням иерархии ученик выполняет все большую часть работы, которую на низших уровнях выполнял учитель. Работа же заключается в том, что либо ученик, либо учитель должны создавать примеры и "почти то", находить различия, выбирать приоритеты, вырабатывать реакции и изменять рассматриваемую модель.