Использование ограничений при анализе сцен
Простейшими задачами для вычислительной машины, снабженной электронным глазом, является выяснение того, сколько объектов присутствует на сцене, каковы их пространственные взаимоотношения, каковы свойства отдельных объектов. Оказалось, однако, что даже такие задачи решать трудно, и удается решить, по-видимому, лишь немногие задачи этого сорта.
В рамках ограниченного мира детских кубиков программы для вычислительных машин сегодня обеспечивают преобразование сигналов от электронного глаза в контурный рисунок, а также перевод содержания контурного рисунка на язык утверждений, говорящих о числе предметов, их взаимоотношениях и свойствах. Однако можно сказать, что только вторая проблема, т. е. проблема использования законченных контурных рисунков, понята достаточно полно. Другая проблема, проблема создания контурных рисунков, даже сейчас полностью не решена.
Здесь мы рассмотрим, каким образом мог бы законченный контурный рисунок, похожий на рис. 3.1, быть проанализирован программой, написанной для вычислительной машины. Будет установлено, что в узлах такие типы линий, как линия разрыва, тени, граница или внутренние линии могут комбинироваться друг с другом лишь небольшим числом способов. Затем мы увидим, что это ограничение задает тип каждой линии на сцене. Когда известны типы линий, легко, опираясь на линии, про которые известно, что они являются граничными, разделить сцену на отдельные объекты, решив тем самым одну из поставленных выше задач.
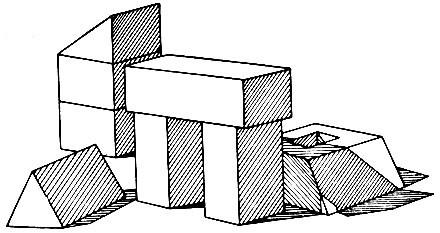
Рис. 3.1. При анализе сцен принимается решение об интерпретации каждой линии рисунка. Сцены, подобные этой, не представляют трудностей для программы Уолца. (Пример заимствован из книги "Психология машинного зрения" под ред. П. Г. Уинстона.- М.: Мир, 1978.)
Линии распадаются на несколько классов
Возьмем для начала многогранник, причем освещение подобрано так, чтобы все тени были устранены. Различные линии на рисунках в этом мире блоков являются представителями различных типов физически существующих краев. Простым и естественным разбиением этих линий является следующее:
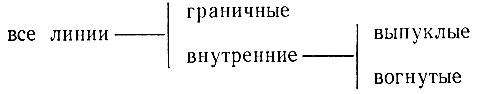
Сначала все линии подразделяются на граничные и внутренние. Граничные линии отделяют области, принадлежащие различным объектам, а внутренние линии отделяют области, относящиеся к одному и тому же объекту. Затем категория внутренних краев под- разбивается на линии, представляющие выпуклые и вогнутые края. С точки зрения обозначений удобно показывать эти типы линий на рисунках с помощью определенных символов. Поскольку такие обозначения будут использоваться достаточно широко, важно сейчас их усвоить.

Направление этих маленьких стрелочек, помещаемых на граничных линиях, определяется тем, какая сторона линии соответствует поверхности загораживающего объекта. Вообразите, что вы движетесь вдоль линии так, чтобы загораживающий объект оставался все время справа. Тогда стрелочка ставится в направлении такого движения.
Теперь естественным образом интерпретируя рис. 3.2 как твердое тело, имеющее форму буквы Г, легко разметить каждую линию так, чтобы правильно отразить ее физическое происхождение. При разметке, таким образом, необходимо опираться на понимание физической ситуации, чтобы получить интерпретацию для каждой из линий рисунка. Основная мысль, которой мы займемся сейчас, состоит в том, чтобы обернуть этот процесс и использовать знание интерпретации линий для понимания физической реальности. Чтобы это сделать, необходимо понять те ограничения на интерпретацию, которые накладываются физическим миром.
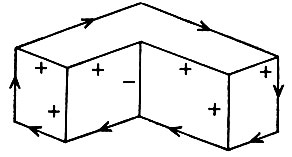
Рис. 3.2. Г-образный предмет, иллюстрирующий три основные интерпретации линий: выпуклые линии, снабженные метками +, вогнутые линии, снабженные метками -, и граничные линии, снабженные метками > или <
В реальных физических вершинах возможны такие соединения ребер между собой, которые могут быть разбиты на классы в соответствии с числом сходящихся линий и с углами между линиями. На рис. 3.3 указаны мнемонические имена, придаваемые обычно используемым классам. К счастью, некоторые простые предположения позволяют сократить этот список до классов СТРЕЛКА, Г, ВИЛКА, Т и упростить объяснения. Эти предположения имеют силу лишь временно и позднее они будут сняты:
Отсутствие тени и разломы (трещины).
Во всех вершинах встречается ровно три поверхности. Этим исключаются объекты, изображенные на рис. 3.4.
Точка наблюдения выбрана в таком месте, что малое перемещение глаза не меняет характера вершины. Следовательно, точка наблюдения, соответствующая рис. 3.5, запрещена.
Эти предположения полезны потому, что они снижают число типов вершин, а следовательно, и число возможных комбинаций для меток линий, исходящих из этих вершин, до приемлемых чисел. Самое важное предположение - это то, что во всех пространственных вершинах встречаются ровно три поверхности, как в углах куба, т. е. эти вершины являются трехгранными. Все изображения, показанные на рис. 3.6, порождены исключительно трехгранными вершинами. Обратите внимание, что все узлы, по-видимому, ограничены четырьмя типами: Г, СТРЕЛКА, ВИЛКА и Т. Ограничиваясь трехгранными углами, мы очевидным образом избежали таких вершин, как К, ПСИ, X, ПИК и КА. Скоро мы убедимся, что это действительно так.
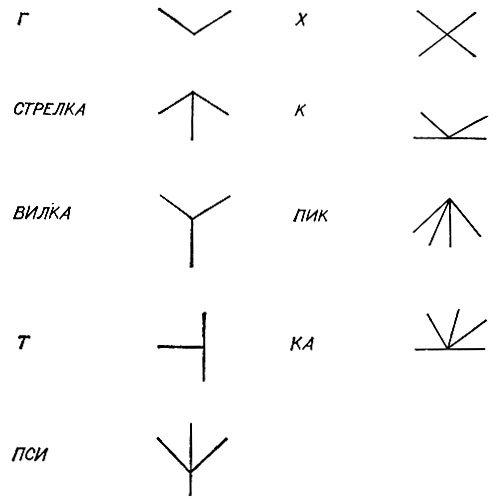
Рис. 3.3. Обычно встречающиеся узлы. Многие из них исключаются, если все вершины трехгранны и нет теней
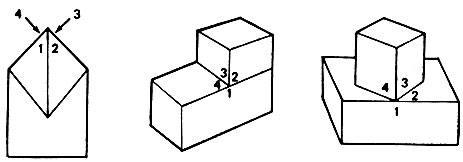
Рис. 3.4. В предположении о трехгранности вершин все эти объекты исключаются из рассмотрения. В каждом из указанных здесь узлов сходятся четыре поверхности
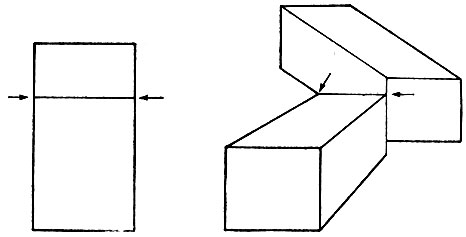
Рис. 3.5. В предположении об общности позиции наблюдателя обе эти конфигурации исключаются, поскольку малое смещение точки зрения радикально изменяет характер указанных здесь узлов
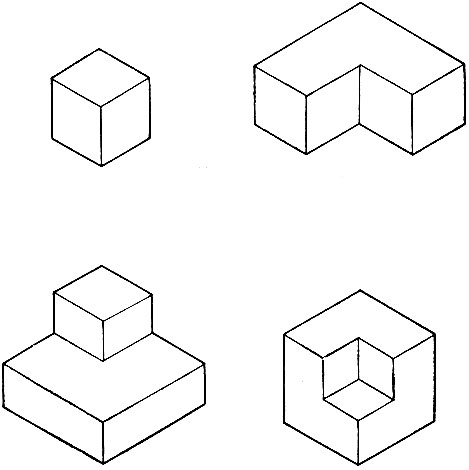
Рис. 3.6. Некоторые объекты, образованные исключительно трехгранными вершинами
Поскольку любую линию можно пометить четырьмя способами, то вершину типа Г можно пометить 42 = 16 способами. Аналогично должно иметься 4 = 64 способа разметить вершины типа ВИЛКА, СТРЕЛКА и Т. Это дает число 208 в качестве верхней границы для числа комбинаций вершин, которое естественно может возникнуть на конкретных рисунках. Любопытно, однако, что реальные вершины могут породить лишь только 18 из этих разметок для линий. Например, при изображении реальных многогранников оказываются невозможными все разметки узла, показанные на рис. 3.7. Наша следующая задача - продемонстрировать, что такие сочетания не реализуемые, и указать те сочетания, с которыми все обстоит нормально. Их всего шесть для Г, пять для вершин типа ВИЛКА, четыре для вершин типа Т и три для вершин СТРЕЛКА. При этом анализ сцены производится так же, как решение задачи составления несложных картинок-загадок из имеющихся кусочков.
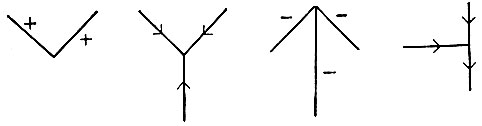
Рис. 3.7. Некоторые комбинации разметок узлов, не встречающиеся при ограничении трехгранными вершинами
В мире трехгранников допустимы лишь 18 различных сочетаний меток
Мы будем рассматривать каждую физически реализуемую вершину со всех возможных направлений с тем, чтобы перечислить все разметки линий, которые можно сделать вокруг узла на контурном рисунке. Это звучит невероятно! Как можно надеяться рассмотреть все возникающие здесь альтернативы? Однако дело в том, что, согласно ограничению, сцены содержат только лишь трехгранные вершины. Три стороны любого трехгранного угла, три плоскости, которые разделяют пространство на восемь частей, как изображено на рис. 3.8, а сам объект, которому принадлежит эта вершина, должен, очевидно, занимать одну или несколько частей.
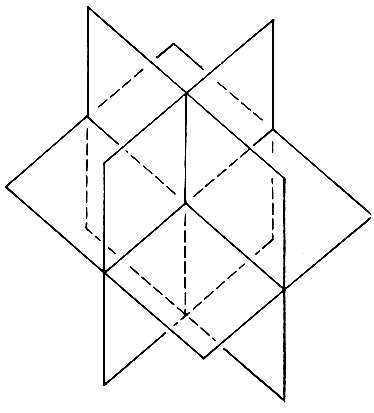
Рис. 3.8. Грани трехгранной вершины разбивают пространство на восемь октантов. Соответствующие плоскости не обязательно должны быть взаимно ортогональными, как здесь изображено
Таким образом, можно с уверенностью определить все возникающие вокруг этого узла возможности с помощью следующего двухшагового процесса: сначала рассматриваются все способы размещения материала предмета по октантам, а затем каждая из результирующих вершин рассматривается из незаполненных октантов.
Конечно, если заполнены все восемь октантов, то нет вершины и рассматривать нечего. Но предположим, что заполнено только семь, как показано на рис. 3.9. Очевидно, в такой ситуации допускается сочетание в узле типа ВИЛКА, в котором каждая из относящихся к нему линий имеет метку "-". Заметим, что во внимание следует принимать лишь узел, находящийся в центре рисунка. Остальная же часть рисунка приведена лишь для того, чтобы легче понять, каким образом семь заполненных октантов образуют узел на этом рисунке. Заметим далее, что поскольку семь октантов заполнены, то имеется ровно один октант, из которого можно взглянуть на вершину. Тип наблюдаемого узла, т. е. ВИЛКА, остается одним и тем же независимо от того, из какой именно точки восьмого октанта рассматривается эта вершина. К счастью, эта инвариантность по отношению к конкретному месту внутри октанта, из которого рассматривается вершина, носит общий характер. Тип узла не изменяется при перемещении точки наблюдения в пределах октанта, хотя при этом углы между линиями меняются весьма значительно.
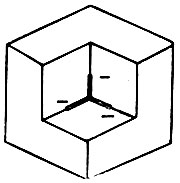
Рис. 3.9. Узел, наблюдаемый тогда, когда семь октантов заполнены. Независимо от положения наблюдателя в пределах единственного оставшегося октанта, видны три вогнутые линии
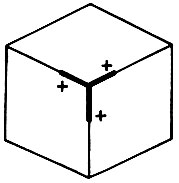
Рис. 3.10. Если заполнен один октант, то наблюдателю из диагонально противоположного октанта видна ВИЛКА, окруженная метками выпуклости. Наблюдения из других шести октантов дают совсем другой результат
До настоящего момента в каталоге возможных узлов находился всего лишь один элемент, а именно ВИЛКА. Если заполнен лишь один октант, то появляются новые элементы. Это иллюстрируется на рис. 3.10, причем, как и раньше, интересующий нас узел окружен частью рисунка, которая служит для того, чтобы понять характер заполнения октанта. Из одной точки наблюдения вершина выглядит как узел типа ВИЛКА, причем каждая линия имеет метку "+". Поскольку заполнен лишь один октант, то имеется семь октантов, из которых можно взглянуть на вершину. Однако до сих пор мы получили лишь такое сочетание меток, которое наблюдается при взгляде из октанта, противостоящего исходному, содержащему сам объект. Следует обратиться еще к шести октантам. Три из них - это те положения, которые занимает маленькая фигурка в первой части рис. 3.11.
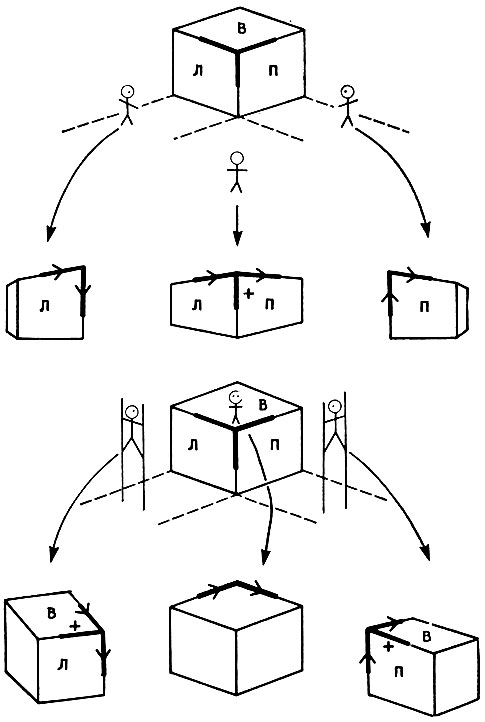
Рис. 3.11. Маленькие фигурки помогают увидеть, как выглядит однооктат ная вершина из различных точек наблюдения. С учетом симметрии семь октантов наблюдателя дают лишь три различные разметки, одну вершину типа Г, одну вершину типа ВИЛКА и одну - типа СТРЕЛКА
Эти фигурки снабжены ходулями для случая двух из трех оставшихся октантов, чтобы приподнять их над плоскостью верхней грани куба. Последняя точка наблюдения задается фигуркой, находящейся сверху, (см. вторую часть рис. 3.11.) Все шесть точек наблюдения, определяемые указанными фигурками, вместе привносят лишь два новых расположения разметок в узлах, поскольку три из них приводят к одному типу сочетания СТРЕЛКА, а три других- к одному типу сочетания Г. В действительности, этого следовало бы ожидать, учитывая естественную симметрию ситуации.
Теперь рассмотрим ситуации, когда заполнены два, четыре или шесть октантов. Все они исключаются благодаря начальному предположению о трехгранности вершин. Предположим, например, что нужно заполнить два октанта. Если они соседние, то ребра между ними будут представлять трещины, у центральной вершины тогда сходилось бы четыре плоскости предметов и угол бы не был трехгранным. Если эти два октанта не соседние, то они соприкасаются либо в точке, либо вдоль некоторого ребра. В любом случае, как показано на рис. 3.12, у центрального узла будет сходиться более трех поверхностей. Аналогичные соображения позволяют исключить случаи заполнения четырех и шести октантов, оставляя для рассмотрения лишь случаи заполнения трех и пяти октантов.
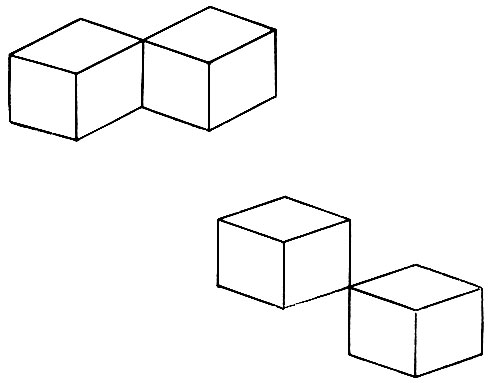
Рис. 3.12. Каждая из этих двуоктантных вершин запрещена согласно предположению о трехгранности (которое на самом деле является предположением о трех поверхностях). В обоих случаях в вершине сходится шесть поверхностей
Относительно трех октантов обратимся к рис. 3.13. Каждый из пяти оставшихся октантов, из которых ведется наблюдение, дает некоторое единственное сочетание. Конечно, здесь изображен лишь один из октантов наблюдения. Здесь вершина видна как СТРЕЛКА. В одном из других октантов она воспринимается как ВИЛКА, а в каждом из трех остающихся - как Г. Каждое сочетание меток в наблюдаемых вершинах Г является уникальным.
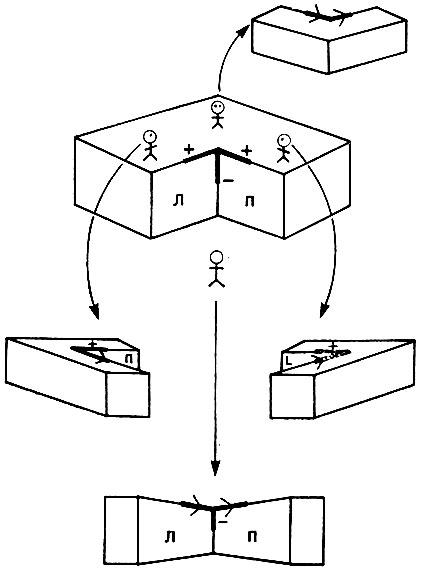
Рис. 3.13. Если заполнены три октанта, то остающиеся для наблюдателя пять октантов дают свою разметку. Это три различные вершины типа Г, одна типа ВИЛКА и одна типа СТРЕЛКА
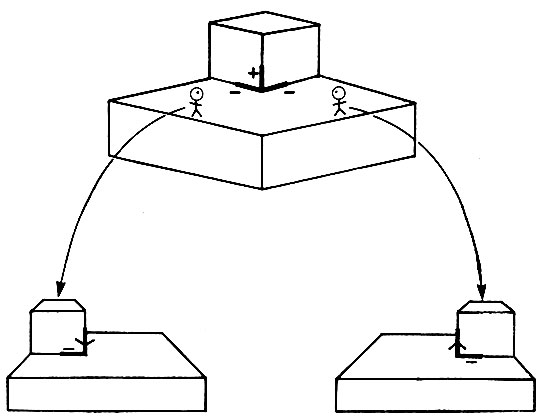
Рис. 3.14. Если заполнено пять октантов, то три остающихся для наблюдателя октанта дают две вершины типа Г и одну типа СТРЕЛКА
Требуется определенная осторожность при добавлении новых сочетаний для вершин типа ВИЛКА, поскольку любая из трех ножек изолированной вершины типа ВИЛКА может нести на себе символ "-". По этой причине наблюдаемые конфигурации в вершинах ВИЛКА порождают три различных элемента в таблице допустимых узлов, несмотря на то что при некотором повороте они выглядят идентично.
На рис. 3.14 показана картина, возникающая при заполнении пяти октантов. Имеется три различных организации узла, каждая из которых отличается от обнаруженных прежде.
Наконец, четыре разметки типа Т возникают при частичном загораживании четырех основных типов линий. Все это вместе дает 18 разметок, которые собраны вместе на рис. 3.15.
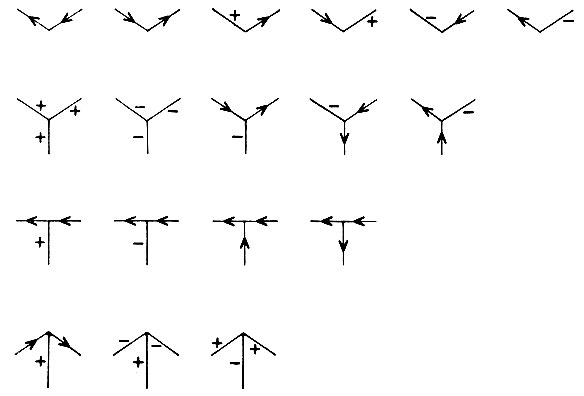
Рис. 3.15. Возможны восемнадцать конфигураций. Если бы не физические ограничения, то их было бы 208
Заметим, что мы перебрали все способы формирования трехгранных вершин и рассмотрели каждую вершину из всех возможных положений наблюдателя. Таким образом, эти 18 сочетаний меток в узлах - это все, что может быть. Всякое сочетание, не содержащееся в нашем списке, не может соответствовать никакой реальной трехгранной вершине!?
Частью анализа сцены является поиск правильных разметок узлов
При исследовании некоторых простых примеров сцен следует иметь в виду три факта, вытекающие из начальных предположений и из учета нашей таблицы:
- На границе, отделяющей группу предметов от фона, имеются лишь метки вида >. Они образуют кольцо по направлению часовой стрелки.
- Имеется только одна СТРЕЛКА с метками > на ее усиках. Для нее древко всегда должно быть помечено символом +.
- Существует всего лишь одна ВИЛКА, у которой имеется хоть один +. На самом деле у нее все линии обязательно должны нести метку "+"
Каким же образом знание о возможной организации узлов может быть использовано при анализе? Этот процесс можно проиллюстрировать на чертеже кубика. Сначала все линии, граничащие с фоном, безусловно, могут быть размечены однородно, как показано на рис. 3.16. Далее основание каждого узла типа ВИЛКА непременно должно получить отметку "+", поскольку уже известно, что усики являются граничными линиями. Остается исследовать лишь центральный узел ВИЛКА. Поскольку все подводящие к нему линии имеют уже отметку "+", полученную в результате предыдущего рассмотрения, то остается лишь проверить, чтобы ВИЛКА с тремя метками "+" имелась в списке физически реализуемых узлов. В данном случае это, разумеется, так.
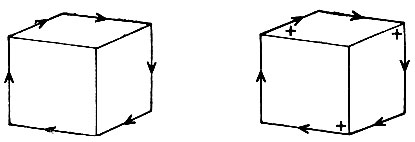
Рис. 3.16. Анализ сцены начинается с размещения вдоль ее границы стрелочек, направленных по часовой стрелке. Далее обычно удобно помечать основания тех стрелок для узлов типа СТРЕЛКА, усики которых оказались лежащими на этой границе
До сих пор мы опирались лишь на те особенно полезные факты, которые были перечислены выше для узлов типа СТРЕЛКА и ВИЛКА. Их было достаточно, чтобы показать, как известные ограничения приводят к тому, что каждая линия получает обязательно интерпретацию, которая в некотором смысле согласуется с естественной интуитивной интерпретацией. Теперь же рассмотрим несколько более трудный пример на рис. 3.17, двухъярусную фигуру, имеющую форму двойного Г. Снова полезно начать с разметки границы между фигурой и фоном. Затем легко перейти к рассмотрению внутренней части, используя особый факт, касающийся узла СТРЕЛКА, два плеча которого помечены как граничные, а также то, что появление одного "+" на узле ВИЛКА обязательно приводит еще к двум меткам "+". Для того чтобы продвинуться дальше, необходимо вернуться к таблице разметок и убедиться, что единственная СТРЕЛКА с меткой "-)-" на ее усике имеет также метку "+" и на другом усике, а древко помечается меткой "-". Точно так же единственная СТРЕЛКА с меткой "-" на усике имеет метку "-" и на другом усике, и на древке. Это с необходимостью ведет к разметке, показанной на рисунке.
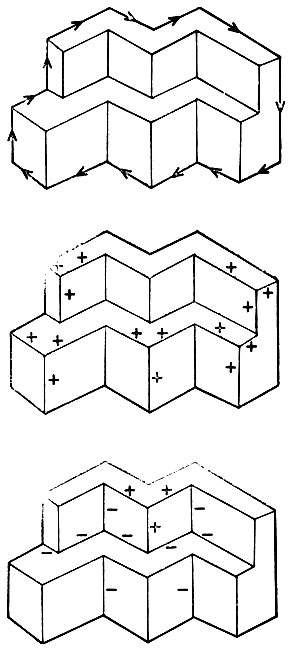
Рис. 3.17. Разметка этой двухъярусной фигуры начинается, как обычно, на границе с фоном. Затем по основаниям стрелок начинают распространяться метки выпуклости, и этот процесс продолжается на всех встречаемых вершинах типа ВИЛКА. После этого процесс завершается разнообразными разметками узлов
Если начинать с внутренних узлов, то возникают большие трудности из-за отсутствия этой априорной разметки граничными символами двух линий. В общем случае несколько интерпретаций оказываются возможными, пока анализ не дойдет до границы, а в этот момент неоднозначность, как правило, исчезает. Это, по-видимому, в той же мере справедливо и для зрения человека, что объясняет определенный класс зрительных иллюзий переворачивания. Рассмотрим на рис. 3.18 укрупненный вариант последней иллюстрации.

Рис. 3.18. Граница с фоном дает значительные ограничения, необходимые для анализа сцены. Если прикрыть этот объект слева и справа, то он попеременно воспринимается то как серия ступенек, то как стопка очень толстых пил
Сосредоточив внимание на центральной зоне, можно видеть либо серию ступенек, либо стопку очень толстых пил, в особенности если прикрыть верх, низ и оба края рисунка. Это может происходить из-за того, что внутренние узлы претерпевают обращение, будучи отделенными от мощных границ либо расстоянием, либо вследствие загораживания рисунка, в результате чего вогнутые, т. е. "-" ребра, кажутся выпуклыми, т. е. "+" ребрами.
Таким образом, наша теория не только содержит те механизмы, с помощью которых вычислительные машины могут анализировать сцены, но и дает правдоподобные объяснения некоторым явлениям, присущим зрению человека. Мы говорили о проблемной области как таковой, вне зависимости от того, кто в ней работает, человек или компьютер.
Интересно отметить также, что эта теория полезна не только для анализа нормальных сцен, то также и для обнаружения неправильно построенных недозволенных сцен, которые не могут соответствовать реальным объектам. Недозволенным является чертеж, изображенный на рис. 3.19, и это заключение можно сделать путем рас- суждений о разметке. Можно по-прежнему использовать фоновые линии, фоновые узлы типа СТРЕЛКА и узлы ВИЛКА с метками "+". Но теперь нет возможности дать разметку линии г. СТРЕЛКА на одном ее конце свидетельствует о метке "-", а Г на другом ее конце требует, чтобы была граничная отметка! (Кстати, то же самое заключение вытекает из наблюдения, что две поверхности встречаются вдоль двух различных линий х и у.)
Следует, однако, с осторожностью подходить к этой идее индентификации недозволенных рисунков. Одно обстоятельство, например, состоит в том, что в изложенной теории допускаются лишь трехгранные вершины. Чертежи, подобные изображению на рис. 3.20, могут представлять нормальные объекты, но они воспринимаются как недозволенные по той причине, что в них присутствуют нетрехгранные вершины. В данном случае при нормальной интерпретации в вершине V сходятся четыре поверхности.
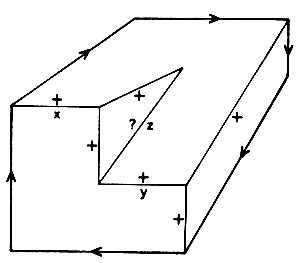
Рис. 3.19. Невозможный объект. Нельзя так разметить линию z, чтобы узлы, расположенные на ее концах, одновременно принадлежали таблице допустимых конфигураций
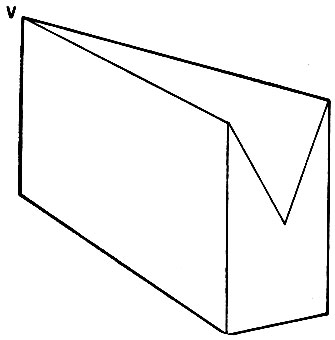
Рис. 3.20. Некоторые нормального вида рисунки не могут быть размечены и следовательно, не могут соответствовать объектам, построенным только с использованием трехгранных вершин
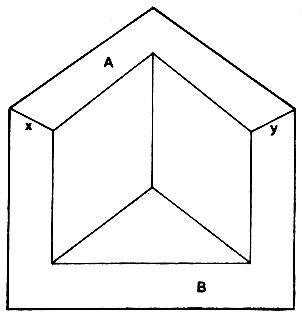
Рис. 3.21. Некоторые рисунки не могут соответствовать реализуемым объектам, несмотря на то что они допускают согласованную разметку
С другой стороны, даже правильно размеченный рисунок может не представлять допустимый объект. Все физически реализуемые объекты с трехгранными вершинами, безусловно, должны давать рисунки, которые могут быть размечены, но наличие размечаемого рисунка, хотя и необходимо для реализуемости объекта, все же не является достаточным условием. Чертеж, изображенный на рис. 3.21, может быть размечен и даже поначалу выглядит вполне нормальным для наблюдателя, но, безусловно, он является недозволенным, поскольку снова две предположительно плоские поверхности А и В встречаются вдоль двух различных линий хну.
В нетрехгранном мире требуется большее число интерпретаций для линий
До настоящего момента мы рассматривали рисунки, считая их как бы подвешенными в воздухе. Но если, скажем, куб может покоиться на поверхности стола, то можно высказать предположение, что лучшей будет такая интерпретация, при которой принимается, что линии внизу скорее являются не граничными линиями, а выпуклыми краями. Однако это не единственная интерпретация, поскольку этот куб точно так же может оказаться приклеенным к стене, как изображено на рис. 3.22. Без дополнительного указания или предположения несколько интерпретаций оказываются равно возможными.
Отметим, однако, что привлечение теней снимает эту неоднозначность. Блоки в центре рис. 3.23 определенно выглядят покоящимися на горизонтальной поверхности, тогда как блоки, расположенные слева и справа, хотя и менее нам привычные, выглядят укрепленными на вертикальной поверхности. Очевидно, расширение нашей теории с тем, чтобы включить в нее метки для обозначения теней, добавляет новые ограничения и упрощает анализ. В самом деле, тени делают набор меток более мощным, и, сделав этот шаг в направлении большей общности, мы можем добавить в рассмотрение также и трещины.
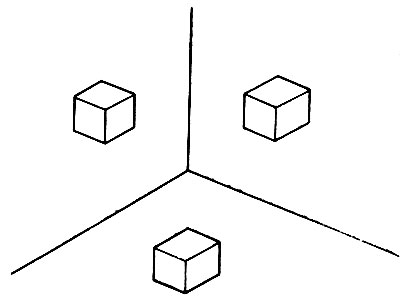
Рис. 3.22. При отсутствии теней имеется несколько вариантов интерпретации кубика: он может либо оказаться подвешенным, либо прикрепленным за одну из его скрытых граней
Обратите внимание, что и граничные и теневые метки указывают направление: граничные метки указывают на область справа как область, которая физически примыкает к границе предмета, тогда как метки тени представляют собой небольшие стрелочки, расположенные так, что они указывают внутрь области тени. Трещины отмечаются символом с.
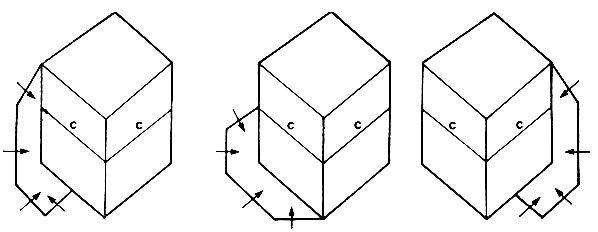
Рис. 3.23. Тени свидетельствуют о том, что один объект покоится на другом. Обратите внимание на метки теней и трещин
Таким образом, наш список, как он выглядит теперь, содержит семь меток: две для граничного и две для теневого края, и по одной для выпуклого, вогнутого края и трещины. Можно было бы непосредственно снова вывести все допустимые сочетания меток в узлах и для этого расширенного списка меток, хотя задача и будет достаточно громоздкой. Проделав эту работу, на примерах можно было бы убедиться, что такое усовершенствование описания приводит к увеличению числа ограничений, вследствие чего возрастает скорость и направленность анализа. Вместо того чтобы это делать, мы зададимся вопросом, если ли еще какие-нибудь другие возможности для разбиения линии на типы. На самом деле они существуют. Сейчас будут описаны два особенно хороших пути. Однако прежде всего не следует забывать о наших целях. Мы стремительно приближаемся к очень большим числам, поскольку множество допустимых комбинаций для узлов будет сильно расти с ожидающимся расширением множества интерпретаций для линий. Станут возможными несколько тысяч допустимых комбинаций в узлах, а не 18, как прежде, и здесь невозможно воссоздать их список или же пытаться промоделировать, что будет делать с ними компьютер. Вместо этого мы сначала выясним, как число допустимых комбинаций растет по отношению к числу недопустимых, а затем обратимся к экспериментальным результатам, которые помогут ответить на вопросы о том, какие улучшения дает это расширенное множество меток и почему.
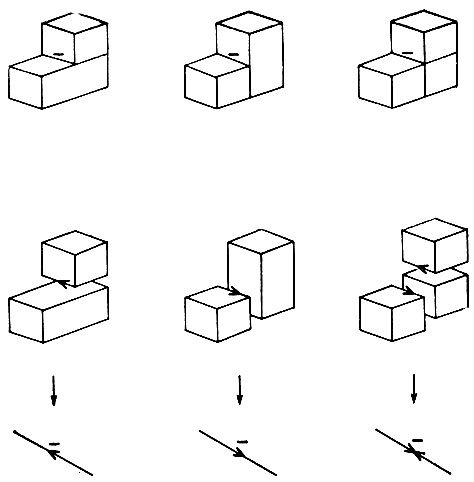
Рис. 3.24. Вогнутые края часто располагаются в том месте, где встречается два и более объекта. Полезно разделить различные случаи, комбинируя метку вогнутости с тем, что будет установлено, если объекты отделить друг от друга
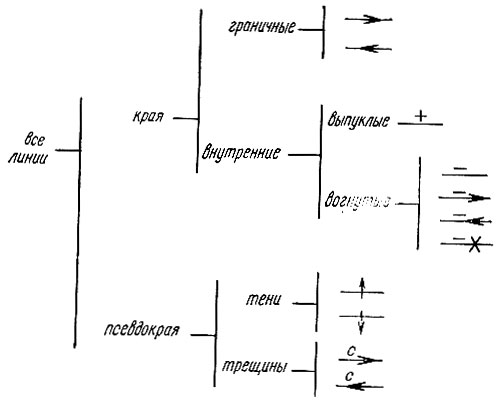
Рис. 3.25. Возможные интерпретации линий и соответствующие метки
Было обещано два усовершенствования выбора типа линий. В первом выделяется тот факт, что объекты чаще всего примыкают друг к другу вдоль вогнутых краев и вдоль трещин. Метки "-" и "с", соответствующие вогнутым линиям и трещинам, могут быть под разбиты на категории, отражающие число предметов и какой из них находится спереди. Предположим, что некоторый вогнутый край символизирует то место, где два предмета примыкают друг к другу. Вообразим теперь, что они немного раздвинуты. Тогда этот вогнутый край становится граничным краем с меткой, указывающей в одном из двух направлений, как изображено на рис. 3.24. Эти две возможности отображаются составными символами, построенными из начальной метки и из новой. Если на самом деле имеется три предмета, то снова используется некоторый составной символ, как показано.
Точно так же анализируются трещины, что в итоге приводит к диаграмме на рис. 3.25, иллюстрирующей одиннадцать возможных интерпретаций линии.
Учет освещенности добавляет ограничение
Второй путь усовершенствования описаний линий связан с освещением. Один из подходов состоит в предположении о том, что условия освещения подпадают под одну из трех категорий, показанных на рис. 3.26: поверхность может быть непосредственно освещенной, может затеняться другим предметом или может быть в тени, потому что она обращена в сторону от источника света. Эти три возможности обозначаются символом О для непосредственно освещенной поверхности, символом 3 для поверхности, затененной другим объектом, и символом СЗ для поверхности, обращенной в сторону от источника, т. е. самозатененной.
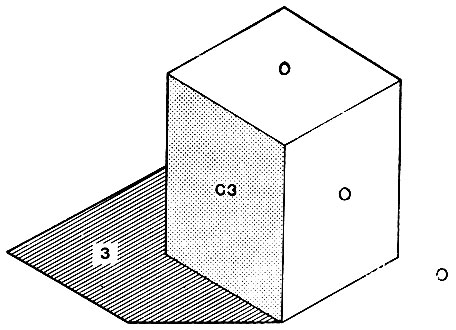
Рис. 3.26. Информация об освещенности также часто поставляет ограничения. При одном источнике света удобно выделять три категории поверхностей: непосредственно освещенную, О; находящуюся в тени от каких-то объектов, т. е. затененную, 3; и самозатененную из-за того, что она обращена в сторону от источника света, СЗ
Метки в добавление к основной информации о типе края могут указывать и на эти состояния освещенности. Если бы состояния освещенности и типы линий могли встречаться в произвольных комбинациях, то было бы 32=9 возможных комбинаций освещения для каждого из 11 типов линий, что дало бы в целом 99 различных возможностей. Но лишь 50 из них оказываются допустимыми. Например, не может быть такой комбинации, когда состояние освещенности меняется при переходе с одной стороны на другую поперек любого вогнутого края. Такая ситуация могла бы встретиться только в случае исключительного совпадения, при котором линия тени проектируется в точности на этот вогнутый край.
Очевидно, что каждое уточнение характера интерпретации линий вносит свой вклад в большое расширение:
- Первоначально предполагались лишь основные типы линий: граничные, а также внутренние выпуклые и вогнутые линии.
- Это число было увеличено при учете теней и трещин.
- Трещины и вогнутые линии были подразделены в соответствии с числом соприкасающихся предметов и в соответствии с тем, как они загораживают друг друга.
- Наконец, информация о типах линий была объединена с информацией об освещенности. Примерно пятьдесят типов образовалось в результате этого заключительного расширения.
Эти изменения значительно увеличили множество физически реализуемых узлов как в смысле первоначальных типов Г, СТРЕЛКА, ВИЛКА, так и новых - К, ПСИ, X, КА, а также других типов вершин, появляющихся в результате ослабления первоначальных требований на трехгранность и на общее расположение. Что же достигнуто? Какие результаты вытекают из разработки и использования этих новых организаций меток в узлах?
Рассмотрим сначала, как можно измерить число физически реализуемых узлов в виде отношения к числу возможных сочетаний меток при отсутствии ограничений. На рис. 3.27 приведены результаты для первоначального множества из четырех возможных разметок. Приведенные проценты указывают на четкое, хотя и не слишком большое ограничение. Однако когда множество категорий линий расширяется, то все числа быстро растут и это ограничение становится просто невероятно заметным. В результате терпеливой работы
по перечислению Уолц пришел к цифрам, приведенным на рис. 3.28. Очевидное ограничение в некоторых случаях приводит к столь малой доле допустимых сочетаний меток в узлах как 9.6×10-6%! Разумеется, общее число сочетаний возросло до слишком большой величины, чтобы их можно было обработать вручную, но все же ограничения оказываются настолько сильными, что вычислительная машина, используя это большое множество, способна выйти на такое решение для сложного рисунка, которое и менее многозначно и достигается гораздо быстрее, чем прежде.

Рис. 3.27. При работе только с основными выпуклыми, вогнутыми и граничными типами линий число организаций меток в узле составляет некоторую долю от комбинаторно возможного числа. Видно, что тип Г дает меньше всего ограничений, а тип СТРЕЛКА - больше всего
Подробности процесса использования этих меток описываются ниже в главе, посвященной альтернативам для стратегий поиска.

Рис. 3.28. Расширение множества интерпретаций путем добавления теней, трещин, отделимых краев и освещенности привносит много больше ограничений. Число физически возможных узлов составляет ничтожную долю комбинаторных возможностей, в особенности для узлов со многими линиями
Здесь же лишь укажем на аналогию с процессом решения системы алгебраических уравнений:
В уравнениях имеется некоторое число переменных, значения которых предстоит определить; в сценах имеются линии, для которых необходимо найти интерпретацию. Значения для алгебраических переменных ищутся с использованием уравнений как источников ограничений. Интерпретации для линий устанавливаются с использованием узлов в той же самой роли источника ограничений.
Эксперименты дают представление о том, что может дать теория
Заведомо ясно одно: программы, основанные на множестве разметок Уолца, успешно справляются со сложными сценами. Например, сцены, приведенные на рис. 3.29, поддаются анализу, несмотря на го что в них встречаются отверстия, совпадения направлений освещенности, особые точки зрения наблюдателя и нетрехгранные углы. Конечным результатом является размеченная сцена, причем тип всех линий либо указан однозначно, либо по меньшей мере ограничен всего несколькими альтернативами.
На основании этой разметки сцена легко разделяется на объекты. Чтобы понять почему, вспомним, что основное множество из одиннадцати интерпретаций для линии содержит семь граничных линий
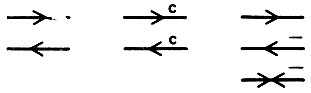
и четыре линии, не относящиеся к границе
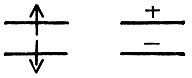
Граничные линии полностью разбивают сцены на совокупность составляющих сцену частей. Прослеживание вдоль граничных линий на последней иллюстрации приводит к выделению объектов, как показано на рис. 3.30.
Описанная процедура не только позволяет решать сложные задачи, из нее видно, что требуемый объем работы для сцены растет грубо говоря, линейно с ростом размера сцены. Если размер сцены измеряется в терминах числа содержащихся в ней объектов, то наблюдавшееся в экспериментах соотношение между вычислениями и сложностью наводит на мысль о том, что влияние конкретных линий и узлов имеет тенденцию не распространяться за пределы той окрестности, к которой они относятся.
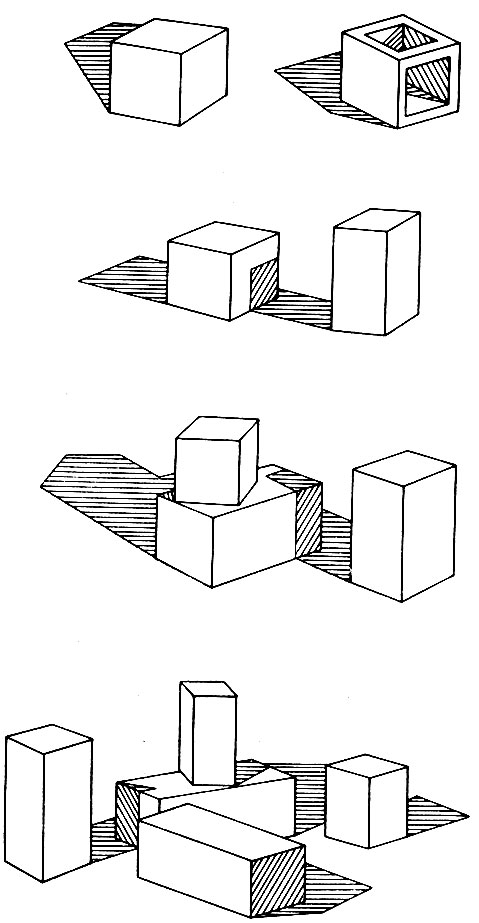
Рис. 3.29. Обобщение основной схемы Уолца позволяет анализировать сцены с отверстиями при наличии совпадений в направлении освещения, наложения вершин и в случае не трехгранных вершин. (Из книги 'Психология машинного зрения'.)
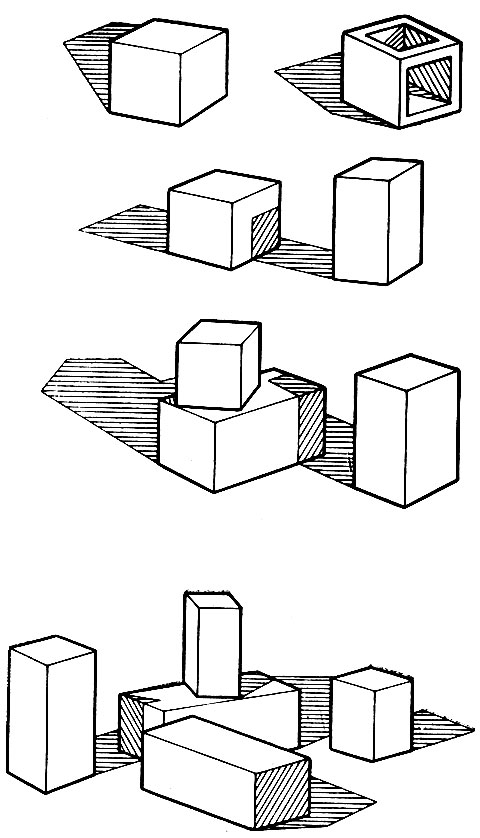
Рис. 3.30. Поскольку при анализе идентифицируются все граничные линии объектов, включая вогнутые линии и трещины, го выделение отдельных объектов является простой задачей. (Из книги 'Психология машинного зрения'.)
Чтобы понять, почему это происходит, предположим, что сцены могут быть каким-то образом разбиты на объемы более или менее фиксированной величины в отношении числа линий и узлов, содер-жащихся в каждом таком объеме. Если объемы таковы, что влияние ограничений не распространяется через их границы, то полное время, требуемое для анализа сцены, очевидно, соотносится линейно с числом объемов, а отсюда и с числом узлов. Что такое разбиение на объемы возможно, подтверждает тот факт, что узлы типа Т, которые чаще всего отделяют один объект от другого, открывают весьма малые возможности для передачи ограничения дальше, поскольку маскирующая граница может оказаться расположенной перед краем любого типа. Если ничего не известно об узле Т на рис. 3.31, а затем выясняется, что поперечина состоит из двух граничных линий, то такая новая информация не дает никаких новых сведений в отношении вертикальной составляющей Т. Если вообще можно однозначно проинтерпретировать линии, то для этого достаточно будет, по-видимому, воспользоваться локальными ограничениями. Это наводит на мысль о том, что если теория позволяет успешно проводить анализ, то это должно происходить за время, пропорциональное размеру сцены. К счастью, эксперимент подтвердил как успех, так и пропорциональную зависимость.

Рис. 3.31. Знание о том, что поперечная линия узла гинь Т имеет определенную разметку, ничего не сообщает о характере продольной линии
Эксперименты показывают, где теория сталкивается с трудностями
Пока что результаты, полученные усовершенствованием интерпретаций для линий, выглядят обнадеживающими. Анализ сцен представляется вполне возможным. Имеется, однако, ряд проблем, выходящих за пределы возможностей тех программ анализа, которые основаны на изложении теории. Эти проблемы обычно требуют проведения глобального рассмотрения.
Первое изображение на рис. 3.32 выглядит вполне безобидным, но оказалось обескураживающим, когда с ним попытались работать. Каким-то образом появились две новые интерпретации: кроме разумной интерпретации с граничными стрелочками, охватывающими стоящий кирпичик, возникли две глупые интерпретации, в которых две из граничных стрелочек были заменены на метки отделимых краев. Программа сошла с ума?
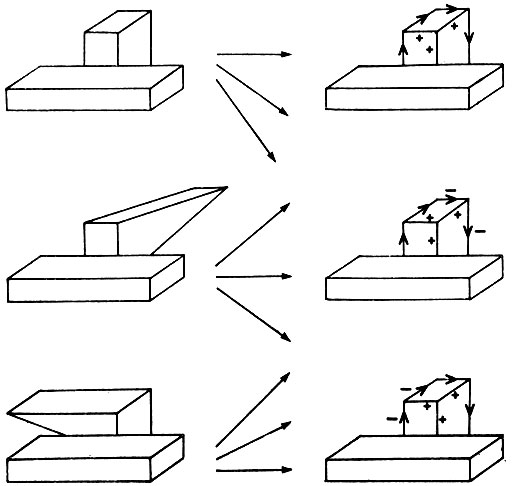
Рис. 3.32. При отсутствии теней в некоторых рисунках никак не удается получить единственной разметки. В приведенном примере все разметки разумны, поскольку сохраняющие узлы искажения приводят к сценам, в которых странные разметки выглядят нормально
Нет. На самом деле было бы плохо, если бы эти две отдельные интерпретации не появились. Последние два изображения на рис. 3.32 поясняют эту мысль. В каждой из приведенных сцен стоящий кирпич искажен так, что он становится лежащим клином. Заметим, что при этом не появляется новых узлов, старые узлы не исчезают и их тип не меняется. Следовательно, ничто не влияет на результат разметки. Процесс абсолютно нечувствителен к изменениям, если только они не влияют на тип узлов или соединений. Программа должна давать тот же ответ и после того, как кирпич превращается в один из этих двух клиньев. А для клиньев интерпретация типа "отделимый край" вполне подходит. Теперь становится ясной причина, по которой первоначальная сцена приводила к трем интерпретациям. Если бы программа давала лишь только интерпретацию, отвечающую стоящему кирпичу, то она оказалась бы более незрячей в отношении клиньев, потому что для нее клинья выглядят в точности так же, как кирпичи*!
* (Правильнее было бы сказать "могут выглядеть, как кирпичи".- Прим. перев. )
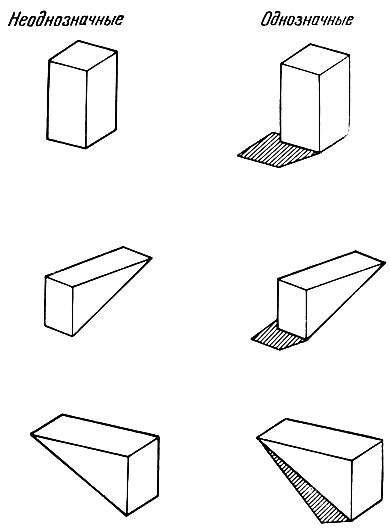
Рис. 3.33. Тени добавляют ограничение и снимают неоднозначность. При отсутствии теней для каждого из этих объектов возможно более одной интерпретации
Одна из причин, по которым эта простая сцена вызывает трудности, состоит в отстутствии теней. Никакой неоднозначности не возникает для объектов на рис. 3.33. Тени дают достаточно ограничений.
В любом случае ясно, что программы, в которых не учитываются детали, связанные с направлением линий и длиной, не могут с гарантией прийти к таким же точным интерпретациям для всех линий, какие удаются людям. На рис. 3.34 показана еще одна задача, подтверждающая этот вывод. Вопрос касается характера области R. Что это - предмет или тень? После некоторого размышления заключение выглядит очевидным. Это должен быть предмет, ибо если бы это была тень, то должна найтись ассоциированная с узлом j вершина, создающая тень. Однако таковой нет. Исходя из других пар узлов, мы знаем направление падения света, и в этом направлении от j нет подходящей вершины, отбрасывающей тень. Здесь снова возникает задача, где требуется учитывать угол и направление, а также знания, касающиеся достаточно удаленных мест. Программа, опирающаяся лишь на сведения относительно локальных комбинаций линий, хотя она на самом деле и весьма эффективна, не может этого сделать.
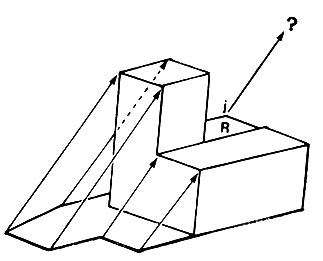
Рис. 3.34. Для решения некоторых задач анализа сцен нужны глобальные рассуждения. Процедура разметки Уолца не может дать ответа, является ли область R тенью или блоком
Результаты Уолца иллюстрируют общий феномен ограничения
Вообще говоря, верно, что более разработанное описание приводит к лучшему и более быстрому анализу. Точнее, вообще говоря, верно, что концентрация внимания на описании атомических единиц в рассматриваемой области позволяет выделить ограничения, которые существенно помогают при анализе. Обращаясь сейчас к языку, мы получим некоторую уверенность в том, что понятие "эффекта Уолца" относится к целому ряду задач обработки информации. В анализе сцен такими атомическими единицами были линии и вершины. При понимании языка это будут группы слов и предложения.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'