Основные методы поиска

Начнем с прокладки маршрута по карте. Рассмотрим рис. 4.3. Предположим, что нам нужно проехать из города S, начального пункта, в город F, конечный пункт, не расходуя бензин зря. Вообще говоря, проблема нахождения хорошего пути требует приложения усилий по двум направлениям:

1. Требуются определенные усилия для нахождения либо какого- то пути, либо наилучшего пути.
2. Необходимо приложить определенные усилия для реальной прокладки маршрута по сети.

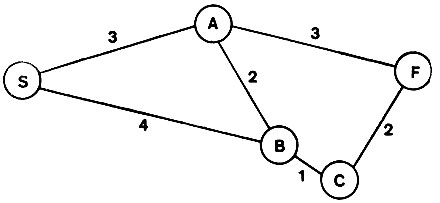
Рис. 4.3. Основная проблема поиска. Необходимо найти путь, ведущий из начального узла к конечному. Поскольку изначально карта дорог решающей программе не сообщается, то она должна провести самостоятельные исследования, чтобы выяснить связи и установить расстояния

Если необходимость перейти от S к F возникает часто, то имеются веские основания для того, чтобы искать действительно хорошего пути. С другой стороны, если эта необходимость возникла только один раз и если для прохождения сети требуются большие затраты сил, то правильнее будет удовлетвориться поиском какого-либо пути, несмотря на то что, выполнив дополнительную работу, можно найти и лучший маршрут. Сейчас мы рассмотрим лишь задачу поиска какого угодно пути. К поиску оптимального пути мы вернемся позже.

Наиболее очевидным способом обнаружения оптимального решения является использование некоторой схемы учета, позволяющей упорядоченным образом исследовать все возможные пути. Полезно отметить, что такая схема учета не должна допускать возникновения циклов на сети. Было бы бессмысленно снова и снова проходить последовательность типа S-А-В-S-А-В... ! Таким образом, сети, на которых предстоит вести поиск, эквивалентны деревьям, наподобие дерева, показанного на рис. 4.4. Это дерево построено на основе сети рис. 4.3 путем просмотра каждого возможного пути, идущего от начальной точки до тех пор, пока на нем не встретится какой-то узел во второй раз.

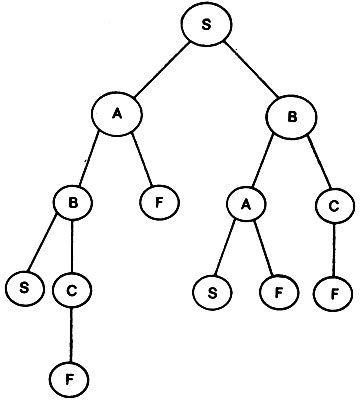
Рис. 4.4. Завершение путей, ведущих в исследованные ранее узлы, преобразует сети в деревья

Заметим, что если ни в один из городов мы не должны попадать дважды, то число ярусов не превосходит я, где n - полное число городов, в данном случае пять. Полная длина каждого пути подсчитывается и отмечается значение минимума. В нашем примере пункт назначения достигается в конце четырех различных маршрутов, длина каждого из которых получается путем сложения небольшого числа расстояний.

Поиск в глубину соответствует нырянию в глубь дерева поиска

При условии, что любой данный путь так же хорош, как и всякий другой, одна из ординарных идей состоит в том, чтобы в каждой вершине выбрать одну из альтернатив и ее исследовать до конца.

Другие альтернативы при этом полностью оставляются без внимания до тех пор, пока сохраняется какая-то надежда прийти в пункт назначения по выбранному направлению. В этом состоит сущность поиска в глубину. Если рассматривать альтернативы в порядке слева направо, первым действием в ситуации рис. 4.5 будет стремительное движение к нижней части дерева по левым его ветвям, показанное пунктирной линией.

Но поскольку оказывается, что первоначально выбранный вариант разрешения предоставлявшихся альтернатив не ведет к вершине F, то следующим шагом будет возвращение назад, в ближайшую вершину с неисследованной еще альтернативной возможностью. Таковой является вершина В. Оставшаяся альтернатива лучше, ибо в конечном счете она ведет к успеху по пути, проходящему через С, как изображено на рисунке. Если бы путь, проходящий через С оказался непригодным, то процедура поиска переместилась бы еще дальше к началу дерева, отыскивая другую подходящую точку ветвления для движения вглубь. По достижении А процесс направился бы вниз, придя отсюда в пункт назначения.

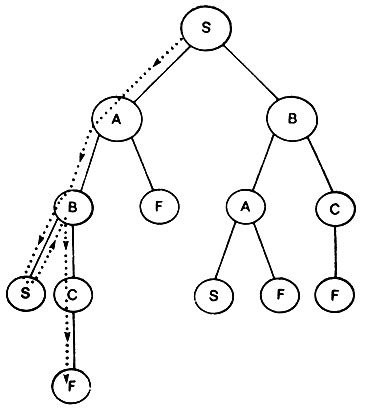
Рис. 4.5. При поиске в глубину выбирается какая-то определенная альтернатива и ее изучение продолжается до тех пор, пока дальнейшее продвижение окажется невозможным. Тогда процесс поиска возобновляется от ближайшей точки ветвления, имеющей неисследованные альтернативные варианты

Сделаем предупреждение: поиск в глубину - это агрессивная, но опасная процедура. Представьте себе более сложное дерево, с гораздо большим числом уровней, чем в нашем иллюстративном примере. Процесс, реализующий поиск в глубину, с большой вероятностью может проскользнуть мимо той ветви, на которой появляется вершина F, и на исчерпывающее исследование расположенных ниже уровня F частей дерева напрасно тратится много сил. Для таких деревьев поиск в глубину, хотя и является легко реализуемым, представляет собой самый худший метод.

Поиск в ширину равномерно продвигается в глубь дерева поиска

Когда поиск в глубину не подходит, может оказаться полезным поиск в ширину. При этом пункт назначения сначала отыскивается среди всех вершин, расположенных на данном уровне, прежде чем будут исследованы ветви, отходящие вниз от этих вершин. В ситуации, показанной на рис. 4.6, В будет проверяться непосредственно по еле А. Затем процесс перейдет на следующий уровень и обнаружит вершину F как раз после того, как будет установлено, что А также ведет к В. Этот подход применим, даже если дерево будет бесконечным или практически бесконечным. Хотя поиск в ширину является осторожным и консервативным, он может оказаться расточительным. Если все пути ведут к пункту назначения, лежащему примерно на одной и той же глубине, то объем работы при поиске в ширину будет больше, чем при поиске в глубину.

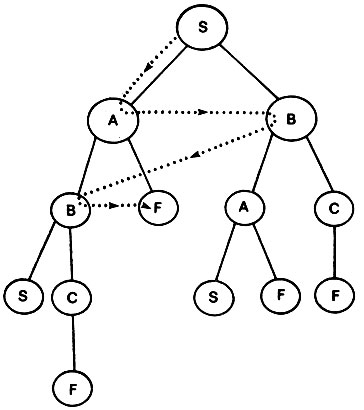
Рис. 4.6. При поиске в ширину всем альтернативам в каждой точке решения уделяется равное внимание. Исследование продвигается по дереву слой за слоем

Полный перебор может быть слишком полным

К сожалению, размер деревьев поиска часто оказывается очень большим, что делает обе процедуры исчерпывающего перебора, и поиск в глубину, и поиск в ширину, в высшей степени непривлекательными. Предположим, что вместо нескольких уровней имеется довольно большое их число. Предположим далее, что ветвление происходит совершенно однородным образом и что число альтернативных ветвей у каждой вершины равно b. Тогда на первом уровне (ярусе) будет b узлов. Для каждого из этих b узлов на втором уровне будет b вершин, т. е. всего b². Продолжая подсчет, приходим к выводу, что в основании дерева будет bⁿ узлов. При прослеживании, например, шахматной партии, величина b порядка 35, а величина n порядка 100 и более. Это означает, что число ситуаций, находящихся в основании дерева всех возможных шахматных ходов, будет порядка 35¹⁰⁰ = 2*5*10¹⁵⁴. Если для подсчетов, связанных с каждой конечной (терминальной) вершиной дерева, требуется одна наносекунда, то для осуществления всей работы потребуется 10 лет! К счастью, в определенных ситуациях можно воспользоваться иными стратегиями, что позволяет резко сократить объем необходимой работы.

Локальные измерения превращают поиск в глубину в процедуру наискорейшего подъема^*

^* (В советской литературе в таком контексте обычно принято говорить о методах наискорейшего спуска.- Прим. перев.)

Эффективность поиска можно повысить самым существенным образом, если имеется некоторый способ упорядочения ветвей, отходящих от каждой вершины, так что в первую очередь рассматриваются наиболее перспективные ветви. Во многих случаях для определения некоторого разумного упорядочения удается использовать определенные замеры. Вот некоторые примеры:

• Войдя в комнату, мы обнаруживаем, что температура является неподходящей. Подойдя к термостату, мы обнаруживаем, что не известно, в какую сторону нужно передвинуть указатель температуры, ибо температурная шкала на приборе оказалась затертой.
• Качество изображения на экране телевизора сильно ухудшилось. Следует подобрать положение ручек регулировки настройки, цвета, оттенков и яркости, добиваясь наилучшего изображения.
• На полпути к вершине горы нас застиг густой туман. Конечно, у нас не оказалось дорожной карты, и не видно подходящей тропы, но у нас есть компас, и мы полны решимости попасть на вершину.

Каждая из указанных проблем соответствует некоторой абстрактной ситуации, в которой имеются определенные регулируемые параметры и способ измерения результата, связанного с каждым конкретным набором величин этих параметров. В одном примере регулируемый параметр - это положение указателя требуемой температуры, а достигаемый эффект - это результирующая степень комфорта. У телевизора имеются разнообразные ручки, каждая из которых взаимодействует с другими, влияя на качество изображения в целом. И разумеется, в примере восхождения на гору регулируемым является положение, а движение происходит вверх или вниз. Именно пример с восхождением и дал название всей процедуре - "процедура наискорейшего подъема". В каждой ситуации мера качества дальнейшего маршрута, Р, зависит от некоторого множества параметров, аналогичных географическим координатам север-юг и запад- восток. См. рис. 4.7.

Рис. 4.7. Метод наискорейшего подъема - это поиск в глубину в сочетании с упорядочением альтернатив в каждой точке, В случае процедуры наискорейшего подъема движение осуществляется по тому из имеющихся направлений, в котором ожидается наибольшее улучшение ситуации, возможное за один шаг. Требуемые измерения могут быть абсолютными, относительными, точными или приближенными

• Такая метафора (наискорейший подъем) диктует следующее правило максимизации: сделать один шаг в каждом стандартном направлении, переместиться в самую высокую из найденных точек и повторять это действие до тех пор, пока не будет найдено место, расположенное выше, чем все четыре окружающие точки, достижимые в результате таких одношаговых проб.

Процедура наискорейшего подъема наталкивается на многие трудности

Трудно придумать что-нибудь проще, чем метод наискорейшего подъема. Но он не всегда применим. Наиболее трагически выглядят проблема холмика, проблема гребня горы и проблема плато.

• С проблемой холмика сталкиваются тогда, когда у горы есть вторичные пики, как на рис. 4.8. Эти вторичные пики как магнитом притягивают к себе наш простейший механизм поиска вершины.

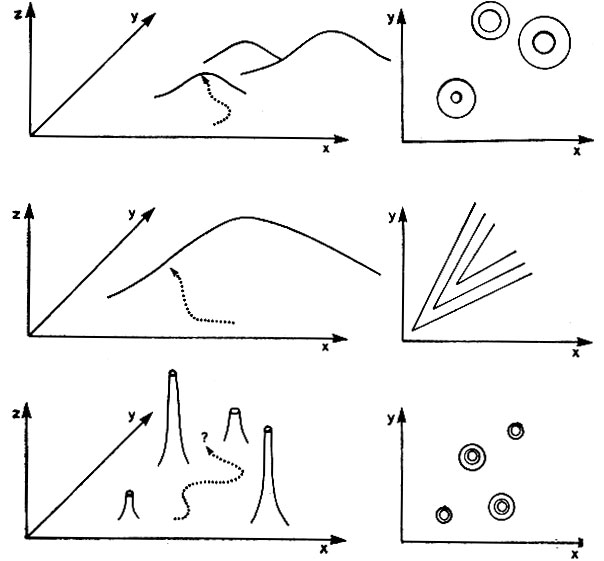
Рис. 4.8. Метод наискорейшего подъема плохо работает на трудной местности* Каждый локальный холмик потенциально является ловушкой. Любая точка гребня может выглядеть как горная вершина, поскольку все пробные направления указывают вниз. Равнинные пространства приводят к бесцельным блужданиям, В каждой ситуации виновата близорукость. Помогает либо более глобальная точка зрения, либо более подходящие пространства

Когда найдена какая-то точка локального максимума, описанная процедура прекращает поиск вершины, считая, что все уже сделано.

• Проблема гребня горы не столь очевидна, а потому приводит к еще большим разочарованиям. Предположим, что мы стоим на чем-то вроде лезвия ножа, простирающегося с северо-востока на юго- запад, как показано во второй части рис. 4.8. Согласно контурной карте, каждый из наших стандартных шагов ведет вниз, хотя мы и не находимся в точке максимального возвышения, ни в глобальной, ни в локальной. Увеличение числа направлений для пробных шагов может в этой ситуации помочь. В задаче о телевизоре это означает, что ручки установки горизонтальной и вертикальной разверток следует вращать одновременно в тех случаях, когда вращение каждой из ручек по отдельности делает изображение странным образом хуже, а не лучше.
• Еще труднее работать в случае проблемы плато. Она возникает тогда, когда пики окружены областью, которая по большей части оказывается плоской. В крайних случаях эти пики могут выглядеть наподобие телеграфных столбов, выступающих на совершенно плоском поле, как в третьей части рис. 4.8. Тогда операции, основанные на локальных улучшениях ситуации, полностью проваливаются. Во всех положениях, за исключением исчезающе малого их числа, при всех стандартных пробных шагах результаты остаются неизменными.

Наискорейший подъем отказывает в случае многомерного пространства

Трудности в случае наискорейшего подъема оказываются мало значительными в одномерных пространствах параметров - обычно мы можем найти некоторый работающий канал в нашем телевизионном приемнике, хотя почти всюду в пределах регулировки настройки изображение отсутствует. Но если бы нам пришлось одновременно точно настраивать две или более регулирующие ручки, то это уже было бы не развлечением, а проклятьем. Если в задаче имеется 20, 30 или более признаков, то ограниченность процедуры наискорейшего подъема становится очевидной.

• Каждая из проблем - холмика, гребня и плато - значительно обостряется по мере увеличения числа параметров.

В некоторых системах используются простые функции качества работы, которые иллюстрируют это обстоятельство. Задачей функций качества работы является объединение данных, касающихся различных аспектов ситуации, и образование единого числа, служащего оценкой в целом. Так часто поступают в простых игровых программах. В шашках, например, данные о различных аспектах позиции обычно включают параметры, связанные с числом шашек, контролем центра, подвижностью фигур и так далее. Самым простым путем сведения их вместе является образование взвешенной суммы:

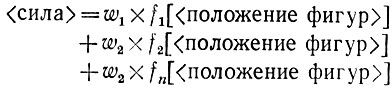
где f_i представляют собой функции от положения фигур на доске, соответствующие различным данным, ω_i - веса.

Процедура наискорейшего подъема представляет собой один из способов нахождения множества весов. Сначала выбирается некоторое начальное множество весов, а затем по мере продвижения игры эти веса изменяются. Задача состоит, конечно, в том, чтобы изменять веса правильно. Если имеется 20 функций f, то мы имеем дело с 20

измерениями, и в каждом узле весового пространства будет 2 × 20 = 40 основных направлений. Опыт показал, что процедура поиска сталкивается со всеми перечисленными выше проблемами, типичными для метода наискорейшего подъема.

Метод наискорейшего подъема может отвлечь внимание от задачи описания и представления

Какие аспекты существенны в задаче? Каким образом эти существенные аспекты могут быть отображены в наборе числовых параметров? Как для данного множества параметров указать функцию качества работы? Это серьезные вопросы, ответа на которые сама по себе идея наискорейшего подъема не дает. Чрезмерное увлечение этим подходом часто ведет к схемам, годящимся только в той ситуации, для которой они были разработаны, что позволяет лишь как-то латать неудачные пространства вместо того, чтобы заняться поиском пространств, в которых перебор оказывается либо достаточно простым делом, либо совсем ненужным. Можно легко увлечься работой, ведущейся в рамках такого подхода. Эта работа требует затраты больших усилий, но, вероятно, сама мысль об использовании взвешенных сумм для оценки игровых ситуаций является убогой.

Процедура наискорейшего подъема в пространстве подобия ускоряет распознавание

С другой стороны, процедура наискорейшего подъема может найти применение в сложных процессах разумной деятельности. Для иллюстрации рассмотрим проблему идентификации неизвестного объекта, принадлежащего миру кубиков, используя имеющиеся описания и различия. Представим себе некоторое множество моделей, образующее некую сеть, как изображено, например, на рис. 4.9. Здесь ребра (графа) связывают пары, которые очень похожи в смысле "почти того".

Теперь предположим, что необходимо опознать неизвестный объект. Что делать, если первое сравнение с некоторой моделью в этой сети окажется неудачным, как и следует, вообще говоря, ожидать? Если различие не оказалось слишком серьезным, если неизвестный объект выглядит похожим на эту модель во многих отношениях, тогда ясно, что в следующую очередь следует испытать модели, про которые известно, что они близки к начальной. Это те самые модели, которые являются соседями данной (т. е. непосредственно связаны с ней ребрами).

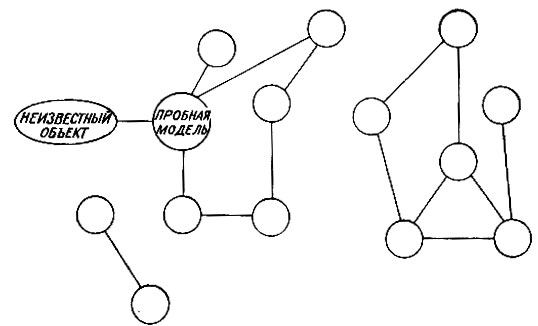
Рис. 4.9. Идентификация неизвестного объекта протекает быстрее, если схожие пробные модели сгруппированы вместе. Если какое-то сопоставление оказывается неудачным, то имеет смысл попробовать близлежащие модели

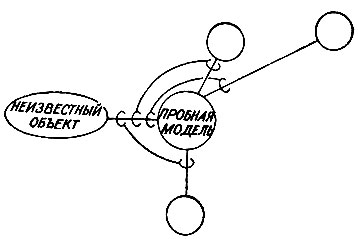
Рис. 4.10. В сетях подобия пробные модели связаны между собой, и сделаны записи о различиях между ними. Если какое-то сопоставление оказывается неудачным, но не слишком неудачным, следующая испытываемая модель отличается от рассмотренной так же, как и неизвестный объект. Таким образом, прохождение по сети моделей направляется неким процессом, основанным на аналогии

Можно ввести очевидное усовершенствование, если ребра не только будут говорить о подобии, но и будут описывать его (точнее, описывать различия), как показано на рис. 4.10. Это не только позволяет произвести выбор следующей тестовой модели из семейства вероятных кандидатов, но также гарантирует выбор некоторого конкретного члена этого семейства, который с наибольшей вероятностью окажется подходящим. Принцип состоит в следующем:

• Если опознаваемый объект отличается от пробной модели точно так же, как от нее отличается некоторый ее сосед, то этого соседа естественно выбрать в качестве следующей пробной модели. В этом смысле неуспех начального сопоставления не является неудачей, но некоторой проверкой знания. Это напоминает метод наискорейшего подъема, поскольку движение по сети моделей определяется различиями между одной моделью и ее ближайшим соседом, который, по-видимому, с наибольшей вероятностью приведет к лучшему соответствию.

Похоже, кстати, что процесс движения по сети связанных моделей близок также и к решению задач на геометрическую аналогию. Представление об аналогии выглядит здесь уместным, поскольку решение о том, какого из соседей использовать при сравнении, определяется на основании описания различий. При решении задач на аналогию мы имеем дело с описаниями различий между рисунками А и В и между С и некоторым X:

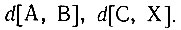
Каждое из этих выражений представляет некоторое правило. Для решения задачи правило, переводящее А в В, сравнивается со всеми другими. Это сравнение само по себе представляет некоторое описание, которое должно быть минимизировано по X.

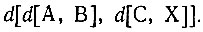
При движении же по некоторой сети подобия имеются описания, относящиеся к неизвестному объекту, U и пробной модели Т, а также относящиеся к различным соседям S и к данной пробной модели.

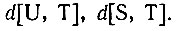
При движении эти описания сопоставляются между собой так, чтобы осуществить минимизацию по S:

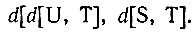
Сходство этого выражения с выражением, относящимся к задаче на поиск аналогии, показывает, что эти процессы носят аналогичный характер.

Процедура поиска от наилучшего частичного пути

В классическом варианте наискорейшего подъема движение вперед всегда производится от последнего решения в сторону дочерней вершины, выглядящей наиболее перспективной. Некоторое небольшое, хотя и важное, видоизменение показано на рис. 4.11. Движение вперед осуществляется из вершины, которая является наилучшей из всех найденных к настоящему моменту, независимо от того, где она располагается в частично построенном дереве. Эта процедура называется поиском "с наилучшего". Она работает как группа альпинистов, кооперирующихся друг с другом в поиске наивысшей точки в некоторой горной местности: они поддерживают друг с другом радиосвязь, двигая вперед всегда наивысшую подгруппу и деля подгруппы на подподгруппы, если дороги разветвляются.

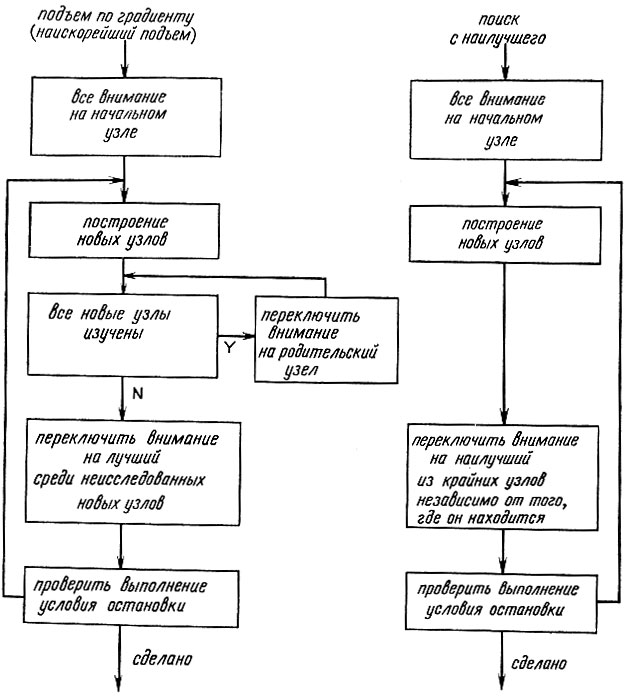
Рис. 4.11. Поиск 'с наилучшего' лишь немного отличается от наискорейшего подъема. При поиске с наилучшего внимание в ходе каждого цикла направлено на наилучший узел в глобальном смысле, тогда как в основном методе наискорейшего подъема оно направлено на наилучший узел, найденный из локальных

Поскольку движение всегда производится в направлении, которое выглядит наиболее перспективным, можно предположить, что общая длина пути решения, найденного этим методом, будет, как правило, ближе к оптимальной, чем у пути, найденного при поиске в глубину или в ширину, когда движение осуществляется рутинным образом, независимо от решаемой задачи. Вообще это так, но не всегда. Ниже мы рассмотрим пример использования схожей идеи в рамках некоторой схемы, гарантирующей обнаружение оптимального пути.

Пробные движения вперед в стратегии ветвей и границ с использованием частичного пути минимальной стоимости

Основная идея проста. Предположим, что требуется найти оптимальное решение для несложного дерева, показанного на рис. 4.12. Посмотрим пока лишь на первый уровень; ясно, что А ближе от S, чем В. Прослеживая путь через А на следующий уровень, ведущий к искомой цели, мы видим, что общая длина этого пути равна четырем. Но тогда незачем вычислять длину альтернативного пути через В, поскольку даже часть этого пути равна уже пяти, т. е. больше длины пути найденного решения через узел А.

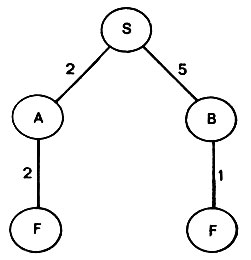
Рис. 4.12. В процедуре ветвей и границ оптимальные пути находятся посредством продолжения в каждом цикле кратчайшего из путей. Здесь работа прекращается, когда продолжен путь, идущий через узел А, поскольку общая длина пути, 4, все еще меньше, чем длина частичного пути, 5, определенная до В

В более общем случае работа схемы такова. В процессе поиска возникает множество неоконченных путей, каждый из которых мог бы быть продолжен дальше. Самый короткий из них тогда продлевается на один шаг, при этом возникает столько новых неоконченных путей, каково ветвление в этой точке. Далее эти новые пути рассматриваются наряду со старыми, и снова продлевается кратчайший из путей. Этот процесс повторяется, пока не будет достигнут целевой узел на одном из путей. Поскольку для продления всегда выбирался кратчайший из путей, то путь, приведший к цели, безусловно, и является оптимальным.

Единственное опасение возникает из-за того, что последний шаг при достижении цели может оказаться настолько длинным, что данный путь решения будет длиннее, чем один или более из незавершенных путей. Может быть так, что один из этих путей отделяет от решения всего лишь незначительный шажек. Чтобы убедиться, что этого не происходит, все незавершенные пути продолжают продлеваться, как и раньше, до тех пор, пока каждый из них не окажется длиннее уже найденного пути решения либо последний не будет низложен.

Вернемся опять к проблеме прокладки маршрута между городами, чтобы посмотреть, как метод ветвей и границ там работает.

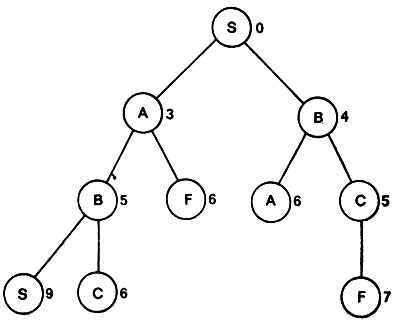
Рис. 4.13. Процедура ветвей и границ дает возможность установить, что путь S-А-F оптимален, поскольку все другие пути были продолжены, пока их длины оказались равными ему или большими

Рис. 4.13 иллюстрирует последовательность, в которой изучаются узлы. На первом шаге А и В появляются как узлы, исходящие из единственного активного узла S. Длина частичного пути до А равна трем, а до В равна четырем, поэтому А становится активным узлом. Затем из А генерируются узлы В и Г с длиной частичного пути, равной 5 и 6. Поскольку теперь известно, что расстояние до Г равно шести, то алгоритм закончит свою работу, как только будет показано, что все другие пути имеют длину 6 или больше. Обе эти возможности проявляются на путях, проходящих далее через В. Один из них с длиной частичного пути, равной 4, продлевается первым, что приводит к пути длиною 6, кончающемуся на А, и к пути длиною 5, кончающемуся на С. Теперь частичные пути, кончающиеся на В и на С, имеют длину пути 5, однако продолжение любого из них приводит к частичным путям длиною 6 или более, так что больше делать ничего не надо. В этом простом примере экономия по сравнению с полным перебором весьма незначительна.

В некоторых случаях поиск может быть значительно улучшен, если воспользоваться предположениями относительно оставшихся расстояний наряду с фактами относительно уже накопленных расстояний. В конце концов, если предположения об оставшихся расстояниях вызывают доверие, тогда это предположительное расстояние в сумме с известным уже пройденным расстоянием должно составлять правдоподобное предположение о полной длине пути:

Ясно, что целесообразно сосредоточить все внимание на развитии пути с самой короткой оцененной длиной, пока оцененная длина пути не возрастет настолько, что будет целесообразно рассматривать вместо него другой путь с меньшим значением оцененной длины. Насколько эта процедура хороша, зависит от степени верности исходных предположений. Если оценки являются точными и безошибочными, то проблемы не возникает. Тогда с самого начала известно расстояние вдоль оптимального пути. Каков бы ни был выбор, отобранная альтернатива будет давать известное минимальное расстояние в качестве оцененной общей длины пути. Однако, как правило, предположения не вполне совершенны, и случайное завышение оценки где-то на действительно минимальном пути может привести к тому, что этот путь будет упущен из виду.

Заметим, что недооценка не может явиться причиной пропуска верного пути. Недооценка величины оставшегося расстояния приводит к недооценке общей длины пути:

Но если путем повторяющегося продолжения маршрута с наименьшими заниженными оценками был найден некоторый полный путь, то больше ничего делать не надо, поскольку очевидно, что истинное расстояние вдоль завершенного неоптимального пути не может быть меньше заниженной оценки расстояния вдоль некоторого незавершенного оптимального пути. Если имеется гарантия, что оценки остающегося расстояния всегда будут заниженными, то минимальный путь будет выбран безошибочно.

При путешествии по сети городов длины авиамаршрутов заведомо являются оценками снизу. На рис. 4.14 показано, что произойдет в рассмотренном ранее примере, если воспользоваться такими оценками. Как и прежде, из S генерируются А и В. Снова для поиска отбирается вершина А, так как для нее нижняя оценка длины пути равна 6, т. е. лучше оценки для вершины В, Заметим, что по иному маршруту А снова ведет к В, а также к F. Но теперь расстояние до F, т. е. 6, меньше оценок снизу длины пути для обоих частичных путей. Поиск завершается, причем экономия затраченных усилий значительна.

Конечно, чем ближе оценка снизу к истинному расстоянию, тем эффективнее процедура. Если они просто совпадают, то никакие ошибочные движения не возможны. В другом крайнем случае, оценки снизу могут оказаться слишком плохими, соответствуя практически нулевым предположениям, и такие оценки для оставшихся расстояний в конечном счете всегда возможны. На самом деле пренебрежение оценками остающихся расстояний всегда можно рассматривать как частный случай оценок снизу, когда они все полагаются равными нулю.

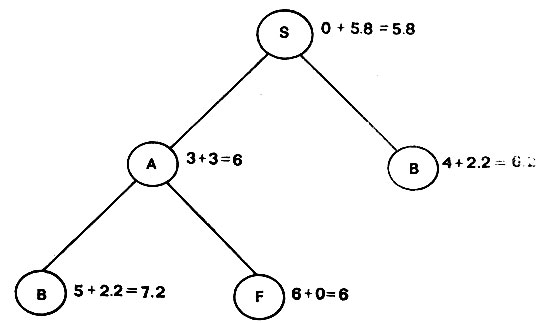
Рис. 4.14. Оценка остающегося расстояния может улучшить работу метода ветвей и границ, но нужно быть уверенным, что эта оценка меньше истинного расстояния, чтобы гарантировать получение нужного результата. Здесь оценкой является расстояние по прямой до конечного узла. Оптимальный путь находится здесь с меньшей затратой усилий, поскольку с помощью нижних оценок общей длины остальные пути завершаются раньше, чем при использовании частичной длины, накопленной к этому моменту

Благодаря деревьям И/ИЛИ решение задач выглядит как поиск

Заканчивая этот раздел, мы полностью отключимся от рассмотрения вопросов прокладки маршрута на карте, чтобы убедиться, что представления о поиске могут быть уместными и в более общем случае решения задач. В частности, мы разовьем здесь мысль о дереве И/ИЛИ, которая следует из двух очевидных эвристик:

• Попытаться преобразовать трудную задачу к ее более простому эквиваленту.
• Попытаться преобразовать трудную задачу к совокупности нескольких более простых подзадач.

Остановимся на первой эвристике. Могут найтись более простые задачи, эквивалентные нашей трудной задаче. Более того, может быть, наилучшим путем решения любой из таких более простых задач является преобразование к еще более простым задачам. Естественным результатом будет еще одна древовидная структура, каждый узел которой соответствует задаче, которую необходимо решить. Такое дерево называется деревом ИЛИ, поскольку все ветви из каждого узла ведут к дочерним задачам, которые дают решение исходной задачи. Достаточно решить любую из дочерних задач. Вообще решение любой из задач, расположенных в нижней части дерева ИЛИ, решает исходную задачу, расположенную вверху, как изображено в первой части рис. 4.15.

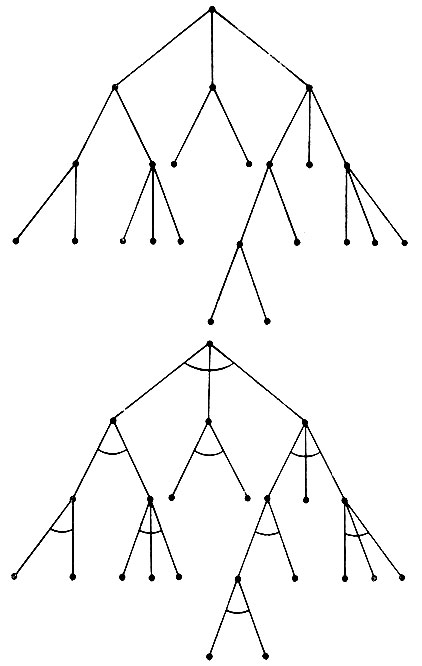
Рис. 4.15. Пример дерева И и дерева ИЛИ. Чтобы решить задачу, расположенную у корня дерева ИЛИ, достаточно решить лишь одну из терминальных задач, но для решения задачи, расположенной у корня дерева И, требуется решение всех терминальных задач

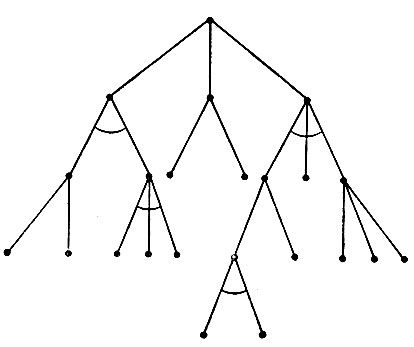
Рис. 4.16. Дерево И/ИЛИ. Для решения задачи, расположенной у корня, достаточно решить одну из многих комбинаций задач, расположенных в основании, поскольку процедура решения может выбрать любую из ветвей, выходящих из узлов ИЛИ, которые встречаются на ее пути по дереву

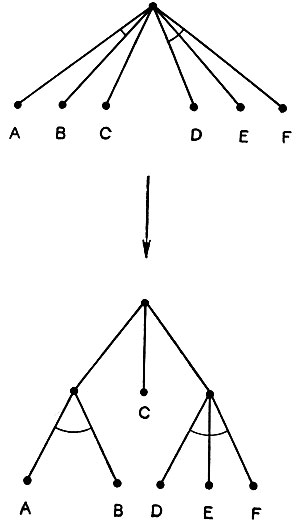
Рис. 4.17. Смешанные узлы И/ИЛИ могут быть разделены на комбинации чистых узлов ИЛИ и чистых узлов И

Вторая эвристика дополняет первую - здесь для решения исходной задачи надо решить все подзадачи. Многократное использование этой эвристики также приводит к древовидной структуре, на этот раз к дереву И, наподобие дерева, изображенного во второй части рис. 4.15. Принято все ветви, выходящие из вершины И, объединять между собой с помощью дуги, подчеркивающей, что эти ветви имеют смысл, лишь если работа ведется сразу над всеми. Заметим, что все задачи, расположенные в нижней части дерева И, должны быть разрешены, прежде чем исходная задача получит решение.

Конечно, чистые деревья И или ИЛИ встречаются редко. На самом деле типы узлов могут произвольно перемешиваться, давая деревья, подобные дереву, изображенному на рис. 4.16. Безусловно, можно разбить задачу на несколько различных множеств подзадач, которые приведут к созданию узлов со смешанным свойством И/ИЛИ. Однако из соображений изящества таких смешанных узлов избегают, вставляя в дерево дополнительные узлы типа ИЛИ. Рис. 4.17 показывает, как это делается.

Деревья И/ИЛИ представляют собой совокупности чистых И- узлов, которые показывают, как задачу можно преобразовать к эквивалентному множеству подзадач, и чистых узлов ИЛИ, показывающих, как задачу можно преобразовать к одной из некоторого множества эквивалентных задач.

Дерево И/ИЛИ обычно показывает, что решение первоначальной задачи, расположенной вверху, может быть получено при помощи нескольких различных совокупностей подзадач. Структура дерева И/ИЛИ интересна тем, что она характеризует как конкретную задачу, которая сейчас рассматривается, так и класс задач, к которому она принадлежит.

Обычно дерево И/ИЛИ отличается очень большими размерами, и одна из задач в процессе решения состоит в том, чтобы избежать построения полного дерева. Следовательно, по мере роста дерева нужно решать, над какими из его терминальных задач следует начать работать, а какие сводить к другим задачам. Поскольку решения такого типа можно принимать с использованием приемов, напоминающих метод наискорейшего подъема или процедуру "лучший в первую очередь", то благодаря деревьям И/ИЛИ решение задач выглядит как поиск (перебор). Однако нужно соблюдать осторожность. Рассмотрение решения как задачи поиска может отвлечь внимание от попыток улучшения в описании проблемы, которые позволят сделать этот перебор тривиальным. Поэтому отложим дальнейшее обсуждение решения задач до следующей главы, где это будет более уместно, и перейдем здесь к рассмотрению других видов поиска.