Распространение меток на сетях

Теория Хаффмана - Клюса анализа контурных рисунков представляет еще одну область, подходящую для поиска. Этот поиск по своему духу полностью отличен от методов, ориентированных на деревья, которые были объектом нашего рассмотрения до сих пор. Напомним, что задача состоит в том, чтобы выяснить, все ли линии на данном рисунке можно интерпретировать так, чтобы все получившиеся сочетания в узлах принадлежали списку из 18 сочетаний, которые, как известно, физически возможны; они еще раз приведены на рис. 4.18. Решение опирается на так называемый поиск с построением диапазона.

Обычный поиск не удовлетворителен для поиска меток линий на рисунке

При проработке произвольных рисунков время от времени будут встречаться ситуации, в которых более чем одно сочетание меток совместимо с интерпретациями, принятыми для ранее исследованных соседних узлов. Возникает выбор. Одна из разметок может привести к тому, что анализ будет завершен на физически возможных сочетаниях меток, тогда как другие ведут к серьезной неудаче, когда некоторые из вершин не удается пометить допустимым образом. Можно считать, что здесь имеется некоторое дерево различных возможностей и надо прибегнуть к поиску (перебору). Заметим, что форма этого дерева определяется порядком, в котором исследуются узлы на рисунке. Иногда удается рассмотреть узлы в таком порядке, который всякий раз обеспечивает принятие определенного решения. Каждый узел в таком дереве поиска имеет лишь одну ветвь!

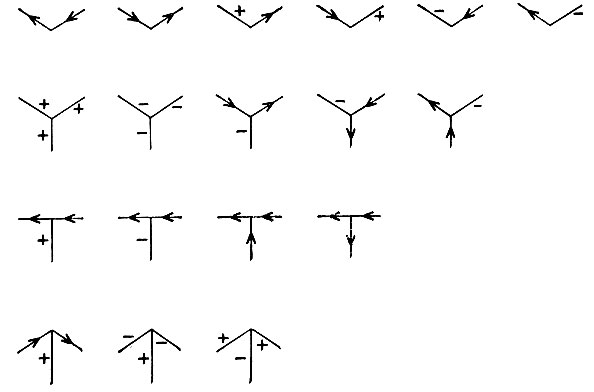
Рис. 4.18. Комбинации меток в узлах для физически реализуемых трехгранных вершин. Символ '+' обозначает выпуклые ребра, символ '-' обозначает вогнутые ребра, а стрелка - границу

Грустно то, что так случается не всегда. Предположим, например, что необходимо разметить неразмеченные линии фрагмента рисунка, изображенного на рис. 4.19. Нет ни одного узла, для которого бы соседи навязывали определенный выбор сочетания меток. В узлах А, В и С, например, имеется по две альтернативы, которые показаны на рисунке. В этих условиях предположим, что узлы рассматриваются в алфавитном порядке А, В, С, D, Е, F и G. Первое дерево на рис. 4.20 отражает варианты выбора, которые возникают при анализе этой ситуации. Такое упорядочение узлов приводит к некоторому ветвящемуся дереву. Если бы порядок был A, D, В, Е, С, F и С, то дерево бы упростилось и приняло бы вид, показанный справа на рис. 4.20.

Другой пример возникает, если на ребре куба сделать выемку, как на рис. 4.21. С учетом всех ограничений, возникающих благодаря рассмотрению распространения меток от внешнего края, все-таки остается два варианта выбора меток для А и для В. Наличие этого выбора ведет к древовидной структуре, в которой два решения получают право на существование.

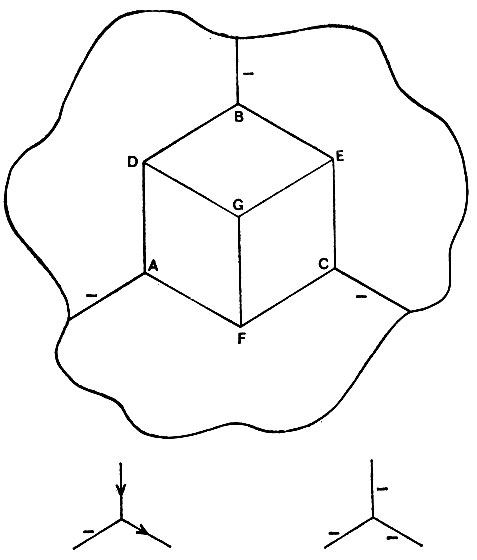
Рис. 4.19. Может не оказаться ни одного узла, в котором выбор меток предопределен. На представленном здесь фрагменте контурного рисунка имеет место именно такая ситуация, поскольку меток '-', расположенных на всех соединительных линиях, недостаточно для однозначного выбора решения. На каждой из трех вершин типа ВИЛКА остаются возможными две комбинации меток. Необходим поиск

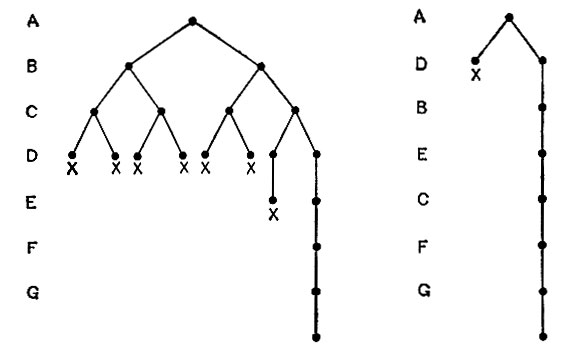
Рис. 4.20. В случае нанесения меток размер и форма дерева поиска определяются тем порядком, в котором рассматриваются узлы. Здесь показано, что одно упорядочение дает гораздо больше ветвей, чем другое

Рис. 4.21.Иногда расположение меток приводит к неустранимой неоднозначности. В показанной ситуации распространение меток прекращается на том этапе, когда встречаются две вершины типа СТРЕЛКА, поскольку каждую из них можно разметить, используя одну из двух показанных комбинаций. Дерево поиска и полностью размеченные рисунки показывают, что обе комбинации являются удовлетворительными сочетаниями меток, хотя лишь одна из них физически оправдана.

В алгоритме Уолца осуществляются итерации, направленные на получение согласованных разметок узлов

Теоретически правильное решение можно было бы найти, используя поиск в ширину или поиск в глубину, но для сцен существенного размера эти методы становятся неэффективными из-за фактора комбинаторного взрыва. К счастью, есть иной метод, в котором особое внимание уделяется понятию выделения и исключения тех сочетаний меток в узлах, которые с очевидностью не верны.

Представьте себе список возможных разметок для каждого из узлов. Эти списки создаются при первом посещении узла, и они уточняются всякий раз, когда изменяется соседний узел. Первое посещение начинается с рассмотрения физически допустимых организаций меток. Каждое из сочетаний, найденных в этом множестве, переносится во множество возможностей для рассматриваемого узла, если оно согласуется по крайней мере с одной возможностью в списках возможных сочетаний для каждого из соседних узлов.

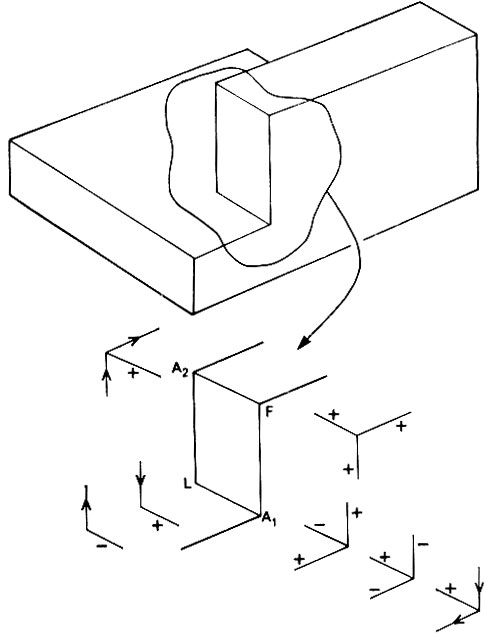
Рис. 4.22. Уолцем была предложена процедура разметки сцен, основывающаяся на построении горизонта. Здесь указан такой порядок рассмотрения вершин: A₁, L, А₂, F. Когда мы впервые попадаем в А₁, то от соседей не поступает никаких ограничений, и приходится рассматривать все три возможности из библиотеки возможностей. Однако когда рассматривается L, то ограничения, совместимые с имеющимися разметками для А₁, исключают четыре разметки, в результате чего остаются лишь две указанные здесь разметки. Они в свою очередь оставляют лишь одну возможность для вершины А₂. В А₂ постоянный пересмотр соседей вначале дает эффект, сказывающийся и на L, и на А₁

Предположим, например, что в рисунке, подобном рис. 4.22, скрыты два узла типа СТРЕЛКА, одна ВИЛКА и один узел типа Г. Предположим далее, что эти четыре узла отделены от рисунка и подвергнуты анализу. Произойдет следующее:

Если узел А₁ типа СТРЕЛКА посещается впервые и до того ни один соседний узел не исследовался, то первым шагом будет принять во внимание все физически возможные разметки узла типа СТРЕЛКА.

Предположим, следующим посещается узел Г. В словаре для узлов имеется всего шесть возможных комбинаций меток для узла вида Г, но лишь две из них согласуются с возможностями, известными для соседнего узла А₁ типа СТРЕЛКА. Следовательно, остальные четыре можно тотчас же отбросить.

Разместив метки для Г, следующим шагом будет исследовать соседние узлы, которые были рассмотрены ранее, чтобы увидеть, что можно отбросить с учетом этих новых меток для Г. В нашей ситуации ничего не произойдет, поскольку все три разметки узла СТРЕЛКА в А₁ согласуются с тем, что имеется у Г.

При переходе к А₂ наш словарь по-прежнему дает три варианта, как и раньше, но для этого узла типа СТРЕЛКА лишь один из них согласуется с уже проанализированными соседями. Другие два немедленно отбрасываются.

Последний раз, когда сосед узла, посещенного вновь, был подвергнут пересмотру, ничего не случилось. Однако на этот раз свежий взгляд на Г показывает, что только одна из оставшихся разметок согласуется с соседним узлом А₂ типа СТРЕЛКА.

После пересмотра списка для Г следует пересмотреть также и соседний узел А₁. Из трех первоначальных возможностей теперь оказывается пригодной лишь одна.

Наконец, обращаясь к узлу типа ВИЛКА, мы видим, что благодаря ограничениям, поступающим от любого из проанализированных соседей, должны быть отброшены все, кроме одного из пяти вариантов, перечне иных в словаре возможностей для узла типа ВИЛКА.

Даже тогда, когда эти четыре узла оказываются выделенными из контурного рисунка и подвергаются независимому анализу, имеющихся ограничений достаточно для обеспечения единственной интерпретации для каждой линии.

Поток ограничений по сцене с большим числом узлов может носить поистине драматический характер, когда принимается во внимание не карликовое множество Хаффмана - Клюса, а гигантское хмножество меток Уолца. Возрастающее число возможностей, допустимых в каждой вершине, несомненно, делает непригодным обычный поиск в глубину, даже распространение ограничений становится слишком сложным для моделирования вручную.

Почувствовать, что происходит, лучше всего можно, посмотрев кинопленку^*. При отсутствии фильма, рассматривая сцену на рис. 4.23 и приведенную там распечатку, можно также получить некоторое представление о том, как работает алгоритм в случае небольшой сцены.

^* (В лаборатории искусственного интеллекта МТИ несколько лет назад был отснят кинофильм, показывающий последовательные этапы смены разметок на одном контурном рисунке,- Прим. перев.)

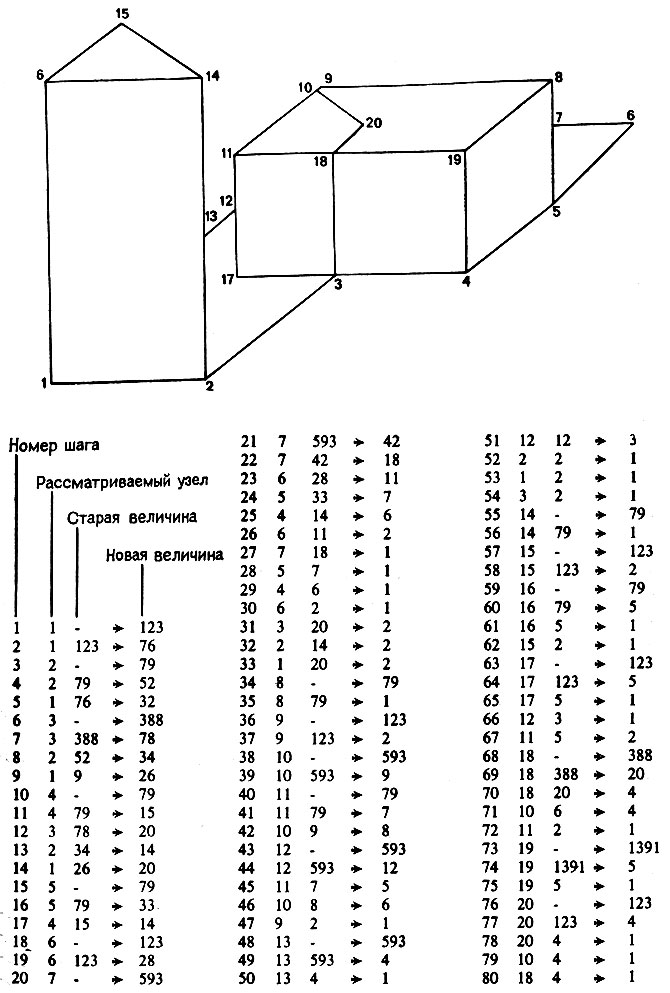
Рис. 4.23. С помощью процедуры Уолца сцена обрабатывается весьма быстро. Номера узлов указывают порядок, в котором некоторая эвристическая процедура посещает узлы в первый раз. Обратите внимание на начальную фокусировку внимания на границе сцены, а также на высокую скорость сходимости

Отметим, например, что принятый способ нумерации узлов гарантирует, что граничные узлы будут рассмотрены в первую очередь. Благодаря этому принимаются во внимание дополнительные ограничения, накладываемые такими узлами. Дальнейший анализ показывает, что сходимость и на самом деле довольно быстрая. После двух или трех посещений для большинства узлов остается лишь одна возможная для них разметка. Для узла 19, например, изначально имеется 1391 возможность, и это число сводится к 5, благодаря ограничениям, поступающим от одного из соседей, а затем благодаря ограничениям, связанным с другим соседом, возникает одно-единственное окончательное значение.

Заметим, что после того, как каждый узел был посещен впервые, следует пересмотреть всех его соседей с тем, чтобы убедиться, что все указанные там возможности еще справедливы. И если у соседей есть изменения, то в свою очередь следует проверить их соседей и так далее, пока распространение влияний не останавливается где-то на узлах, в которых ничего не происходит, ни одна из прежде указанных возможностей не исчезает.