Действия при наличии противника

Еще один тип поиска связан с работой над играми, предмет, интерес к которому не ослабевает. В отношении игр, подобных шахматам, шашкам и восточной игре Го, у некоторых людей возникает ощущение, что едва ли необходимы какие-то знания, выходящие за рамки того, что необходимо для просмотра вперед на несколько своих ходов и ответных ходов противника, чтобы представить себе возможные последствия каждого допустимого хода. Другие же заявляют, что блестящая стратегическая игра не может быть основана исключительно на просмотре вариантов, и несомненно больше требуется в направлении понимания и реагирования на различного рода позиционные ситуации.

Противоположность интересов в играх придает игровым деревьям своеобразный характер

До настоящего момента теория и практика выделяли аспект просмотра вариантов, возможно, по той причине, что предмет поиска поддается изучению. Узлы в дереве поиска обычно представляют игровые ситуации. Они связаны между собой посредством ходов, преобразующих одну ситуацию в другую. Рис. 4.24 иллюстрирует это. Разумеется, здесь возникает новая особенность, состоящая в том, что решения принимаются двумя людьми, действующими как противники и принимающими свои решения по очереди.

Реальные игры содержат в себе гораздо больше, чем те два хода, которые показаны в нашей игре. Среднее число возможных ходов, даваемое статистикой, известно как коэффициент ветвления.

Рис. 4.24. Игры порождают среду поиска с новым свойством - соперничеством. Как здесь показано, узлы представляют игровую ситуацию, а дуги - связывающие их ходы

• Коэффициент ветвления - это среднее число допустимых ходов, возможных в данной позиции игры.

Именно сопоставление коэффициента ветвления и среднего числа ходов в игре в общем случае показывает абсурдность просмотра вариантов до конца игры. В шахматах, например, оправданной оценкой для коэффициента ветвления является что-то около 35, и нормально каждый игрок совершает около 50 ходов. Ясно, что 35100 - слишком большое число.

Меньший объем знаний ведет к большему объему поиска

Если бы только имелся какой-то хороший способ ранжирования элементов множества игровых ситуаций, то было бы просто указать ход, который ведет к наилучшей ситуации, из тех, что достижимы за один ход. К сожалению не существует ни одной такой формулы ранжирования ситуаций. Если ситуации на доске отличаются заметным образом, то некоторая простая мера, наподобие подсчета числа фигур, могла бы стать основой некоторого грубого описания качества, однако использование такой меры для ранжирования ходов ведет, неплохим результатам. Необходима какая-то иная стратегия.

Очевидным обобщением было бы использование оценки для ситуации на доске не сразу же, а после того как игра продвинется на один или более циклов, состоящих из ходов одного и другого партнера. Здесь нельзя идти слишком далеко, так как очень скоро комбинаторный взрыв приведет к немыслимо большим числам, но если остановиться на некоторой разумной глубине, то путем сопоставления терминальных ситуаций друг с другом, возможно, удастся составить критерий выбора ходов. Конечно, в основе такого подхода лежит: предположение, что достоинства ситуации проясняются при развитии игры и что процесс просмотра вариантов может быть продолжен так далеко, что оказывается удовлетворительной даже самая грубая оценка ситуации на доске. Это предположение является предметом острых дебатов.

Для просмотра вариантов необходимо статическое оценивание и минимаксная процедура

Если сравнению подвергаются лишь ситуации, достижимые за один ход, то упорядочение ситуаций по рангу вполне годится. К сожалению, оно непригодно в контексте перебора вариантов в игре, поскольку тогда необходимы некоторые абсолютные, а не относительные стандарты. Наблюдалась тенденция суммировать все соображения с помощью одного числа, характеризующего качество в целом. Это было продиктовано желанием воспользоваться простыми стратегиями, к изучению которых мы готовы приступить, но отображение качества в целом с помощью одного числа обладает серьезным недостатком.

• Число не сообщает ничего о том, как оно было получено. Это очень бедный способ суммирования. Часто мы применяем его лишь потому, что слишком слабо представляем себе, что надо делать. Это плохо.
• Принято, чтобы положительные числа указывали на преимущество одного игрока, а отрицательные - другого. Степень этого преимущества соответствует абсолютной величине числа, оценивающего позицию в игре.
• Процесс определения числа, характеризующего качество ситуации, называется статическим оцениванием. В конце некоего ограниченного изучения возможных ходов с помощью устройства статического оценивания создается статическая оценка.

Игрок, старающийся получить положительные числа, называется максимизирующим игроком, а его оппонент - минимизирующим. Если ход совершает максимизирующий игрок, то он ищет путь, ведущий к большому положительному числу, и он будет предполагать, что оппонент попытается направить игру в сторону ситуаций со строго отрицательными статическими оценками.

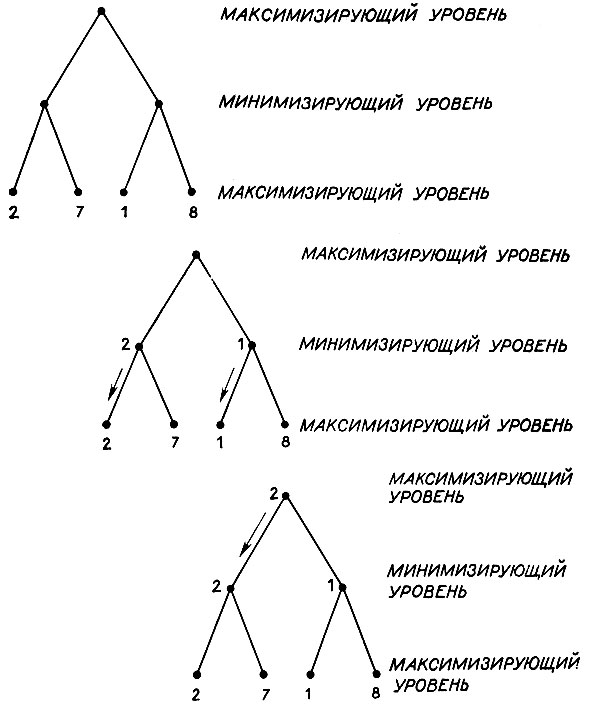
Рис. 4.25. Минимаксная процедура представляет собой способ выбора ходов на основе частично построенного игрового дерева при использовании статической оценки, которая позволяет охарактеризовать ситуацию одним числом, отражающим степень превосходства. Один из игроков добивается наибольших чисел в игре, а другой стремится к наименьшим

Так, в стилизованном миниатюрном игровом дереве на рис. 4.25 максимизирующий игрок может надеяться на получение ситуации со статической оценкой, равной 8. Но он знает, что минимизирующий игрок этого не позволит, так как он может выбрать ход, уводящий игру в сторону ситуации, оцененной в 1. В общем, решение максимизирующего должно учитывать реакцию минимизирующего игрока на следующем ходе. Если просмотр вариантов идет дальше, то минимизирующий игрок, несомненно, ходит с учетом выбора имеющимся у максимизирующего игрока на следующем уровне. Это продолжается до тех пор, пока не будет достигнут предел изучения и система статического оценивания не создаст прочную основу для выбора между различными альтернативами. В нашем примере статические оценки в основании показывают, что выбор, доступный минимизирующему игроку, дает оценки, равные 2 и 1, на уровне как раз на один выше того, где проводятся эти статические оценки. Знание этого счета предполагается, когда минимизирующий игрок выбирает свои ход, поэтому максимизирующий игрок может определить наилучшую игру на один уровень выше. Ясно, что он перейдет к узлу, в котором минимизирующий игрок не может получить оценки меньше чем 2. Снова оценка на одном уровне определяет действие и итоговую оценку на один уровень выше.

• Процесс, в котором информация о счете распространяется по игровому дереву, называется минимаксным, так как счет в узле является максимумом или минимумом счета в узле, расположенном под ним.

Заметим, что этот процесс может быть весьма дорогим по двум причинам: во-первых, дорогим может оказаться вычисление статических величин для всех возможных путей, во-вторых, даже сама генерация всех возможных путей может оказаться камнем преткновения. Что обходится дороже, зависит от деталей системы статической оценки и использованного генератора ходов.

Альфа-бета-процедура позволяет уменьшить дерево поиска

С первого взгляда может показаться, что статическая оценка должна быть проведена для каждой ситуации, находящейся в основании дерева. Хорошо, что это не так. Имеется процедура, которая позволяет уменьшить как размер дерева, которое должно быть построено, так и число необходимых статических оценок, таким образом уменьшая полный объем необходимой работы. Она несколько напоминает метод ветвей и границ в том, что удается показать неоптимальность некоторых из путей, хотя они и не просматриваются до пределов, устанавливаемых в переборе вариантов.

Рассмотрим ситуацию, изображенную в верхней части рис. 4.26, где система статической оценки уже была использована для первых двух терминальных ситуаций. Минимаксные рассуждения для счета 2 и 7 показывают, что минимизирующий игрок может гарантировать себе ситуацию со счетом 2, если максимизирующий игрок будет при-держиваться правой ветви, выходящей из вершины дерева. Этим в свою очередь гарантируется, что максимизирующий игрок не может поступить хуже, чем направить игру в сторону счета 2. Это становится ясным до того, как будут проделаны другие статические оценки, поскольку максимизирующий игрок, безусловно, может выбрать эту изученную ветвь, если другие окажутся хуже. Это показывает верхний узел дерева в средней части рис. 4.26.

Теперь предположим, что следующий узел был оценен, в результате чего был найден счет, равный 1. Видя это, минимизирующий игрок, безусловно, не может сделать для себя хуже, чем получить 1, по тем же причинам, по которым в верхнем узле максимизирующий игрок не мог сделать для себя хуже, чем получить 2. Но теперь лишь смысл слова "хуже" поменялся. На уровнях максимизирующего игрока хуже означает получение меньших чисел, тогда как на уровнях игрока минимизирующего - больших.

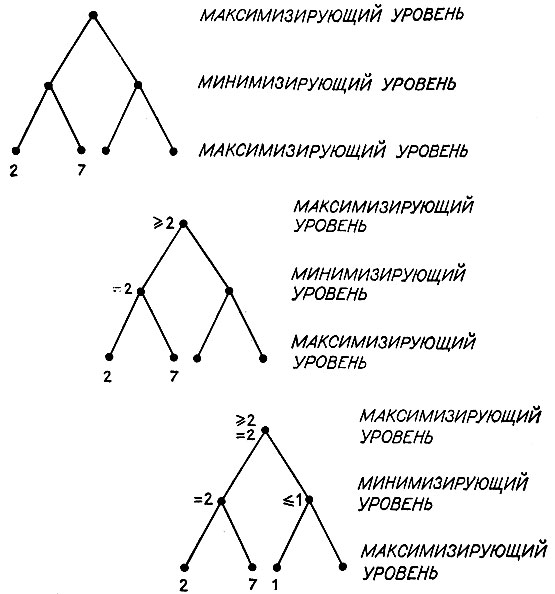
Рис. 4.26. Объем работы можно несколько уменьшить, комбинируя идею минимакса с процедурой альфа-бета. Здесь показано, что полностью исследовать правую часть дерева нет необходимости, поскольку это никак не отразится на выборе хода. Как только обнаружено, что движение вправо хуже движения влево, уже нет смысла изучать, насколько оно хуже. В общем случае использование альфа- бета-процедуры означает и уменьшение числа применений генератора новых ходов, и меньшее число статических оценок

Посмотрим на дерево внимательнее. Есть ли смысл переходить к ситуации на доске, соответствующей последнему узлу? Может ли оказать какое-то влияние система статической оценки в этом узле? Хотя и странно, но ответ здесь отрицательный. Поскольку максимизирующий игрок с уверенностью знает, что он не придет к ситуации худшей, чем 2, если он пойдет по левой ветви, то о правой части ему не надо знать ничего, кроме того, что на ней он не сумеет добиться лучшего, чем 1. Оценка последнего узла может быть равной + 100 или -100, или чему угодно, и это никак не скажется на полученном результате.

После анализа становится ясно, что был использован следующий ключевой принцип:

• Если у оппонента есть хотя бы один ответ, который показывает, что потенциальный ход является плохим, то нет необходимости устанавливать, какие другие ответные ходы возможны на рассматриваемый потенциальный ход. Если где-то заклинило, то нет смысла выяснять, многими ли способами, или насколько плохо в наихудшем случае. Этот принцип составляет основу альфа-бета-методики. На практике эта процедура сводится к следующим двум видам деятельности:
• Всякий раз, когда что-то устанавливается относительно лучшего, на что можно надеяться в данном узле, проверить, что известно о родительском узле. Может быть так, что ниже данного узла уже ничего делать не надо.
• Всякий раз, когда для данного узла удается получить точную оценку, проверить, что известно об узлах, расположенных выше. Возможно, самое лучшее, на что можно надеяться в начальном узле, может быть подвергнуто пересмотру или установлено точно.

Сейчас уместно посмотреть, как методика альфа-бета работает в более серьезном примере. К сожалению, на бумаге несколько трудно показать, как статические оценки перемежаются с заключениями, касающимися качества узлов. Фильм или устное пояснение были бы более адекватны, но за их отсутствием мы обойдемся тем, что в кружках поместим порядковые номера событий, располагая их рядом с заключениями, которые говорят о порядке, в котором они были сделаны. Так сделано на рис. 4.27, где представлено другое стилизованное дерево, в каждом узле которого имеется три ветви.

• 1-2: Двигаясь по левой ветви по каждой из точек решения, поиск доходит до основания дерева, где устанавливается статическая величина 8. Это значение явственно указывает на то, что максимизирующий игрок не может сделать для себя ничего хуже с оставшимися тремя вариантами, чем получить значение 8. Отметка об этом размещается на шаге 2.
• 3-5: Чтобы убедиться, что ничего лучшего, чем 8, нельзя найти, максимизирующий игрок исследует два других доступных ему хода. Поскольку 7 и 3 говорят о менее удачных ходах, то он приходит к заключению, что достижимый счет равен в точности 8, и верным является как раз тот ход, который был рассмотрен первым.
• 6: Фиксация счета максимизирующего игрока на самом нижнем узле позволяет сделать вывод о том, на что может рассчитывать минимизирующий игрок в узле уровнем выше. Поскольку известен один ход, который ведет максимизирующего игрока к счету 8, то минимизирующий игрок не может прийти к ситуации хуже чем 8.
• 7-8: Чтобы убедиться в том, что минимизирующий игрок способен добиться лучшего на втором уровне, должны быть исследованы два оставшихся его хода. Первый ведет к ситуации, в которой максимизирующий игрок может получить по крайней мере 9. Здесь дерево обрывается. Выбрав левую ветвь, минимизирующий игрок добивается счета 8, а выбрав среднюю, он получит не лучше, чем 9, а может прийти и к худшей ситуации, если другие выборы мак-симизирующего игрока будут давать большие величины. Поэтому средняя ветвь оказывается плохой для минимизирующего игрока, нет необходимости продолжать анализ дальше, чтобы установить, насколько плохой она может быть, и, следовательно, нет необходимости в двух статических оценках. Наихудшая ожидаемая величина для минимизирующего игрока - это по-прежнему 8.
• 9-14: Минимизирующий игрок все же должен оценить свою последнюю возможность, ту, что связана с правой ветвью. Следующие шаги связаны то с оценками, то с заключениями относительно ситуации максимизирующего игрока прямо над исследуемыми узлами. Вывод состоит в том, что счет для максимизирующего игрока равен 4.
• 15: Открытие, что правая ветвь ведет к счету 4, позволяет минимизирующему игроку остановиться на правой ветви, поскольку 4 лучше 8, первоначальной нижней оценки.
• 16: Теперь может быть установлена некоторая граница для исходного узла. Максимизирующий игрок после рассмотрения возникающей здесь ситуации видит, что левая ветвь ведет к счету 4. Теперь он знает, что это он получит во всяком случае. Чтобы установить, может ли он добиться лучшего, необходимо рассмотреть среднюю и правую ветви.
• 17-22: Решение о том, как минимизирующий игрок будет реагировать в конце средней ветви, требует знания, что произойдет вдоль левой ветви, отходящей отсюда. Здесь максимизирующий игрок в состоянии установить, что лучшей будет игра, ведущая к позиции со счетом 5.
• 23: Пока не будет известно что-то определенное относительно того, что мог бы сделать максимизирующий игрок, нельзя указать никаких границ на потенциальные возможности минимизирующего игрока. Знание же, что максимизирующий игрок получит 5 на левой ветви,- это уже знание чего-то определенного. Заключение состоит в том, что минимизирующий игрок обеспечивает себе оценку не хуже чем 5.
• 24-27: При анализе того, что может сделать максимизирующий игрок ниже средней ветви минимизирующего игрока, обнаруживается путь, на котором максимизирующий игрок может достигнуть счета 9. Но 9 - это плохо, если учесть тот факт, что у минимизирующего игрока имеется одна возможность, гарантирующая ему 5. Дерево снова обрывается. Нет смысла исследовать другие максимизирующие возможности, благодаря чему не нужно делать лишней статической оценки.
• 28-29: Рассмотрение правой ветви минимизирующего игрока быстро приводит к выводу, что и она также дает максимизирующему игроку шанс провести игру с худшим счетом по сравнению с тем, которого минимизирующий игрок может достичь на левой ветви. Здесь обрыв дерева позволяет избежать двух статических оценок.
• 30: Поскольку ветвей для исследования не осталось, то граница 5 для счета минимизирующего игрока перестает быть границей, а становится реально достижимой величиной.
• 31: Максимизирующий игрок в высшей точке дерева, видя наибольшие перспективы в средней ветви, временно на ней останавливается и теперь знает, что он может добиться счета не хуже чем 5.
• 32-37: Теперь следует изучить правую ветвь для максимизирующего игрока в высшей точке. Углубляясь в дерево, перемещаясь немного вперед и назад, приходим к заключению, что минимизирующий игрок убеждается, что выбор левой ветви обеспечивает счет 3.
• 38: Минимизирующий игрок может заключить, что счет, достигаемый на левой ветви, является границей того, насколько удачно он может поступить.
• 39: Зная, что минимизирующий игрок может направить игру к ситуации со счетом 3, максимизирующий игрок у верхнего узла дерева заключает, что нет смысла исследовать правую ветвь дальше В конце концов счет 5 является результатом движения по средней ветви. Заметим, что благодаря этому экономится не только шесть статических оценок, но и два применения генератора хода, что может быть весьма ценным само по себе.

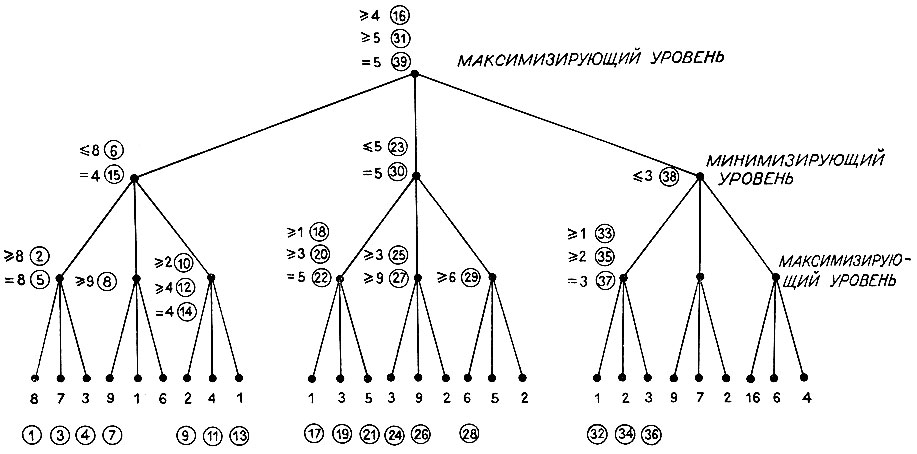
Рис. 4.27. Игровое дерево глубины три с коэффициентом ветвления, равным трем. Цифры в кружочках указывают порядок, в котором делаются заключения. Вместо 27 статических оценок, необходимых, когда не применяются усечения с помощью альфа-бета-процедуры, теперь их требуется всего лишь 16. Очевидно, что наилучшим продолжением для максимизирующего игрока будет игра, развивающаяся вдоль средней ветви

Нетрудно потеряться в этом примере. Даже бывалые специалисты по играм ощущают определенное волшебство, таящееся в методике альфа-бета, всякий раз, когда они обращаются к ней после долгого перерыва. Каждое отдельное заключение как будто правильно, но результат в целом выглядит странно. Позже, когда будет продемонстрирована одна простая программа, реализующая усечение дерева поиска в соответствии с альфа-бета-процедурой, все это покажется уже более естественным.

Заметим, между прочим, что в этом примере никогда не возникала необходимость подняться более чем на один уровень выше для того, чтобы решить, следует ли закончить изучение дерева. Это объясняется исключительно небольшой глубиной использованного дерева. В случае деревьев глубиной в четыре или более уровней могут встретиться так называемые глубокие усечения, для которых требуется более глубокий просмотр дерева.

Альфа-бета-процедура может оказаться малоэффективной

Важно хорошо себе представлять, что можно ожидать от альфа- бета-процедуры. Один из путей к этому - изучение наилучших и наихудших случаев.

В худшем случае эта процедура не приводит ни к чему. Легко построить дерево так, чтобы систему статической оценки пришлось применять ко всем терминальным ситуациям.

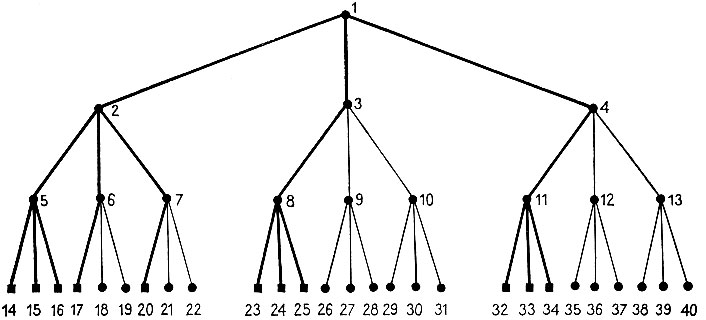
Рис. 4.28. В полностью упорядоченном дереве процедура альфа-бета приводит к уменьшению вдвое величины показателя экспоненты, характеризующей комбинаторный взрыв. Это происходит из-за того, что нет необходимости рассматривать все варианты ходов партнера, чтобы оправдать выбор левой ветви. Полное упорядочение дерева с глубиной, равной трем, и коэффициентом ветвления, равным трем, уменьшает число требуемых статических оценок с 27 до 11

Для рассмотрения наилучшего случая, однако, необходимо некоторое усилие. Предположим, что благодаря везению или по другой причине дерево упорядочено таким образом, что каждый наилучший ход каждого игрока связан с самой левой альтернативой в каждом узле. Тогда наилучшим ходом игрока, находящегося в верхней точке дерева, является левый. Однако сколько раз ему необходимо проделать статическое оценивание, чтобы получить уверенность, что этот ход наилучший? Чтобы разобраться в этом, рассмотрим дерево глубины три и коэффициентом ветвления, также равным трем, на рис. 4.28.

Предполагая, что наилучшие ходы игроков всегда расположены слева, значение для самого левого хода максимизирующего игрока, находящегося в верхней точке дерева, является той статической оценкой, которая характеризует ситуацию на доске, отвечающую самой левой точке. Считая это верным, получаем, что максимизи-рующий игрок располагает чем-то конкретным, с чем сопоставляются возникающие перед ним альтернативы. Однако нет необходимости рассматривать все ответы оппонента на эти альтернативы.

• Для проверки правильности хода в данном узле упорядоченного дерева необходимо рассмотреть относительно немного терминальных узлов, соответствующих непосредственным альтернативам для проверяемого хода. Это объясняется тем, что все терминалы, находящиеся ниже не оптимальных ходов оппонента, можно не принимать во внимание.

Почему получается так, что необходимо рассматривать все варианты для игрока, совершающего ход, игнорируя все ходы, кроме одного, его партнера? Это очень неприятный вопрос. Для ответа на него требуется более внимательно рассмотреть нашу основную идею: если партнер располагает некоторой серией ответных действий, которая делает некоторый ход плохим, тогда независимо от других возможных развитий игры этот ход считается плохим.

Ключ к пониманию заключается в словах некоторый и независимо от. "Некоторый" предполагает проверку одного из ходов партнера всякий раз, когда перед ним возникает выбор, а также предполагает, что ход достаточно хорош, чтобы подтвердить заключение. Однако, чтобы быть уверенным в справедливости этого заключения, независимо от того, что мог бы сделать противник, необходимо, конечно, проверить каждую из имеющихся у него альтернатив.

Рассмотрим самый левый ход, ведущий от вершины 3 к вершине 8. Все возможные реакции на этот ход максимизирующего игрока должны быть опробованы, т. е. статическая оценка должна быть произведена в вершинах 23, 24 и 25.

Это дает 8 для максимизирующего игрока, значит верхняя граница для минимизирующего игрока равна 3, что в сравнении с 2 делает бессмысленными исследования ниже узла 3.

Но теперь, каким образом максимизирующий игрок может получить уверенность, что справедлив тот счет, который передается вверх по левому ребру? Ясно, что он обязан убедиться, что разумный минимизирующий игрок в точке 2 выберет самую левую ветвь. Это можно сделать, предположив, что число, поступающее вверх по левому ребру из 5, является верным, а затем максимально эффективно отвергнуть все альтернативы. Однако ясно, что нет необходимости рассматривать все варианты, предоставляющиеся минимизирующему партнеру. Снова ветвление наступает лишь на каждом втором уровне в соответствии с вариантом, который должен быть просмотрен вдоль левого ребра. Статическая оценка должна быть произведена в вершинах 17 и 20.

Наконец, имеется вопрос о предположении минимизирующего игрока относительно числа, поступающего из 5. Для этого требуется рассмотреть все альтернативы максимизирующего игрока - тривиальный частный случай нашего общего соображения,- это приводит к необходимости статической оценки 15 и 16 для того, чтобы убедиться, что статическая оценка, проведенная в 14, дает число, пригодное для передачи наверх.

Таким образом, когда альтернативы располагаются столь удачным образом, из 27 возможных статических оценок требуется сделать лишь 11. В более глубоких деревьях с большим коэффициентом ветвления экономия еще более разительна. В действительности можно показать, что число статических оценок, необходимых для обнаружения наилучшего хода в оптимально организованном дереве, дается выражением

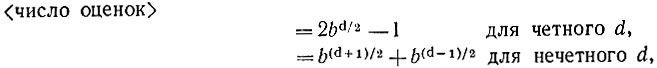
где b - коэффициент ветвления, a d - глубина поиска, выраженная в ходах.

Это выражение может быть проверено прямой индукцией. Необходимо лишь обобщить линию рассуждения, использованную в последнем примере, сконцентрировав внимание на том, что для проверки варианта требуется обследовать лишь каждый второй уровень. Заметим, что приведенная формула безусловно верна для d = 1, поскольку тогда она упрощается до b. Для d = 3 и b = 3 формула дает ответ 11, что, кстати, подтверждает заключение, достигнутое в рассмотренном нами примере.

Будьте внимательны: формула верна лишь для частного случая, когда дерево правильным образом упорядочено. По этой причине данная опенка мало говорит о том, что может быть достигнуто, ибо если бы был какой-то способ упорядочивать дерево так, чтобы лучшие ходы располагались слева, то никакой надобности в альфа- бета-процедуре для усечения дерева не было бы! Но и нельзя сказать, что это наше упражнение было полностью бессмысленным. Формула устанавливает нижнюю границу для числа статических оценок, требуемых в реальной игре. Эта нижняя граница может оказаться близкой к реальному результату, или далекой от него в зависимости от того, насколько хорошо на самом деле упорядочены ходы. Этот реальный результат должен располагаться где-то между худшим случаем, в котором следует оценить b^d терминалов, и лучшим случаем, в котором все же требуется произвести примерно 2b^d/2 оценок терминальных вершин.

В любом случае требуемое число становится невообразимо большим с ростом глубины дерева. Альфа-бета-процедура дает лишь временную отсрочку взрывному, экспоненциальному росту, но не предотвращает его. См. рис. 4.29.

Эвристические приемы также позволяют упростить поиск

Методика ускорения поиска, основанная на альфа-бета-процедуре, гарантирует получение столь же хорошего ответа, как тот, что может быть найден при применении полной, исчерпывающей минимаксной процедуры. Целый ряд других методов такой гарантии не дает, но используется в комбинации с альфа-бета процедурой как дополнительное оружие в борьбе против взрывного характера роста дерева. Широко употребляются следующие методы:

Ограничение ширины. Прямой способ уменьшения эффективного коэффициента ветвления в игровом дереве состоит в том, чтобы опускать менее вероятные возможности. Поскольку тот или иной разумный генератор ходов так или иначе используется в связи с альфа-бета-процедурой, нетрудно выделить лишь наиболее вероятных последователей любого из узлов, которыми следует заняться.

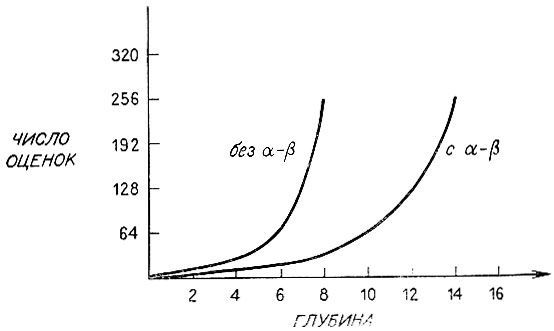
Рис. 4.29. Альфа-бета-процедура уменьшает скорость развития комбинаторного взрыва, но не останавливает его

Несколько обобщая, можно допустить, чтобы ширина варьировалась с глубиной проникновения, возможно смещая усилия в сторону большей перспективности, с помощью формулы типа следующей:

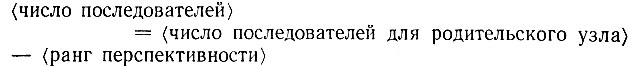
Так, если вершина является сама одной из пяти последователей и по рангу считается второй из наиболее перспективных, то должно быть 5 - 2 = 3 последователя. Полное дерево, построенное на этом привале, принимает суживающуюся форму, как изображено на рис. 4.30.

Нет необходимости говорить, что эвристики тактического ограничения ширины дерева поиска действуют в точности противоположным образом по отношению к тактике, допускающей жертвы фигур для того, чтобы в конечном итоге добиться лучшей позиции.

Поскольку отбрасываются те ходы, которые выглядят на первый взгляд плохими, то маловероятно, что у программ, ограничивающих ширину, будут отмечены какие-то необычайно хорошие ходы, которые в какой-то момент времени представляются явно невыгодными, но впоследствии приводят к компенсации потерь и даже дают преимущество.

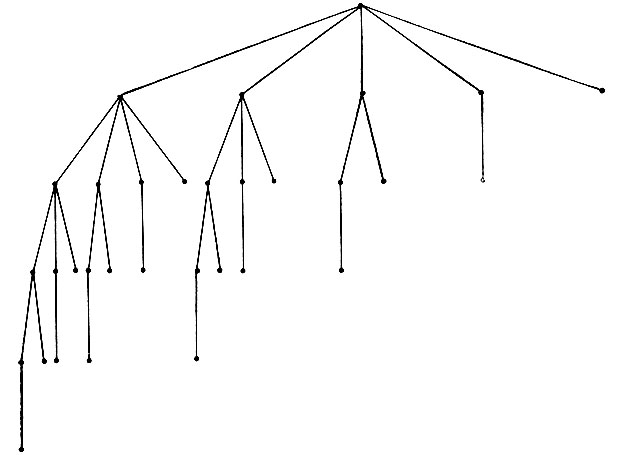
Рис. 4.30. При поиске с уменьшающейся шириной большее внимание уделяется наиболее перспективным ходам. В данном случае такой алгоритм приводит к уменьшению объема поиска по мере возрастания глубины и снижения перспективности

Отбрасывание заведомо неудачных путей. Другая возможность ограничения поиска в направлении плохих ходов базируется не просто на положении хода в смысле ранга его перспективности, а на некоторой аккумулируемой величине перспективности. Благодаря этому размеры и форма дерева становятся зависимыми от конкретной ситуации. Если оправдана лишь какая-то одна линия ведения игры, то лишь ей одной и нужно следовать, а поэтому ее можно просмотреть на большую глубину. С другой стороны, если сразу несколько линий поведения в игре выглядят разумными, то в этом методе обнаруживается тенденция к равному распределению между ними имеющихся ресурсов.

Отбрасывание бесполезных путей. Продление дерева равномерно по ходам с равной перспективностью вполне оправдано. Однако после того, как были получены надежные оценки, может оказаться так, что можно достичь существенного упрощения поиска за счет отказа от частично развитых ходов, которые в самом лучшем случае могут лишь слегка улучшить некоторый полностью изученный ход.

Этот момент иллюстрируется на рис. 4.31. Показанное дерево было уже частично проанализировано. Здесь удобно использовать для обозначения статических оценок не какие-то числа, а величины х и у. Заметим, что у максимизирующего игрока, расположенного в верхней точке, счет заведомо равен x или выше.

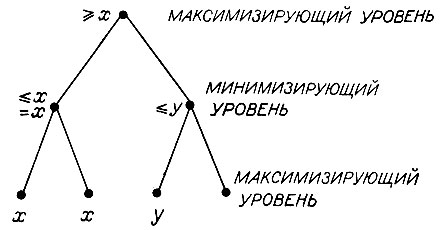
Рис. 4.31. Иногда не имеет смысла заниматься исследованием ветви, которая хотя и может оказаться оптимальной, но приносит потенциально незначительную выгоду. Здесь показан поиск, в котором максимизирующий игрок, придерживаясь левой ветви, получит гарантированную величину, равную х. Неполный анализ правой ветви показывает, что на правой ветви максимизирующий игрок не сможет достигнуть лучшего, чем у. Если у больше, чем х, то процедура альфа-бета не дает усечения, но если указанная разница невелика, то максимизирующий игрок может отказаться от полного анализа, остановившись на удобной для него левой ветви

Предположим теперь, что у больше х, но незначительно. Это главное, о чем нам надо сейчас помнить. Двигаясь в направлении правой ветви от узла, минимизирующий игрок может заставить максимизирующего игрока получить у или меньше, причем меньше в том и только в том случае, если пока не оцененная вершина на самом деле дает счет меньше, чем у.

Теперь, если у больше, чем х, не происходит обычного альфа-бета-усечения, поскольку у минимизирующего игрока нет очевидного основания направить игру в сторону достаточно низкого счета. Но если отличие х от у невелико, то независимо от того, насколько хорошим может оказаться неоцененный узел, потенциальная выгода, достижимая путем такого завершения процесса перебора, оказывается малой. Это верно по той причине, что если этот неоцененный узел очень выгоден, минимизирующий игрок будет его попросту избегать, оставив максимизирующему игроку счет, равный у, имея у - х сверх того, что он, как ему известно, получит, идя по левой ветви. В этом случае вполне естественное решение - двигаться влево, принимая значение* и избегая проведения дополнительной

оценки узла. Кстати, если величина этого неисследованного узла больше, чем х, то полный анализ показал бы, что абсолютно оптимальным путем был бы путь вправо. Но почему же заставлять программу работать, как лошадь, из-за незначительной потенциальной выгоды? Найденный счет, по всей вероятности, будет ниже х, поэтому дополнительная работа будет бесполезной.

Условия для дополнительного наращивания. До сих пор рассматривались методы, ограничивающие рост дерева. Иногда полезно поступить противоположным образом, наращивая дерево, когда этого требует ситуация. Если, например, позиция на шахматной доске очень острая, то имеет смысл продолжать игру, пока не будет достигнуто более спокойное состояние. Имеется целый ряд условий для такого наращивания, которые позволяют рассматривать положение как острое и заслуживающее дальнейшего анализа:

Король в опасности. 
Предвидится размен фигур. 
Пешка проходит в ферзи.

Вторичный поиск. После того как завершен обычный поиск с использованием альфа-бета-процедуры, использованы различные эвристические методы и методы наращивания дерева, часто целесообразно начать строить новое дерево от узла, который завершает вырисовывающийся теперь оптимальный путь. Это позволяет произвести двойную проверку оценки для полученного целевого узла: одно значение дает процедура статической оценки, а другое следует из минимаксного анализа вторичного дерева поиска. При этом мы надеемся, что эти два значения окажутся примерно одинаковыми, подтверждая, что непосредственно за пределами той глубины, с которой велся первичный поиск, никаких сюрпризов не окажется. По-видимому, такая дополнительная глубина практически неприемлема для дерева в общем случае, но допускается в специальном случае, когда необходимо подтверждение оцененного значения для оптимальной линии ведения игры. На рис. 4.32 показано, какую форму может принять дерево, когда используются вместе процедуры дополнительного наращивания и процедура вторичного поиска.

Кстати, сюрпризы, о которых говорилось выше, часто являются следствием ходов, отодвигающих, но не предотвращающих катастрофу. Чтобы показать, как это возникает, предположим, что имеется некоторая комбинация, которая ведет к неизбежному взятию ферзя противника. Предположим теперь, что сторона, теряющая ферзя, может оттянуть момент потери, жертвуя другими, менее важными фигурами. До тех пор пока потеря ферзя неизбежна, задержки, при которых теряются дополнительные фигуры, абсурдны. Однако такие задерживающие ходы могут вывести игру за пределы ограничений на глубину, установленных для дерева поиска. В примере на рис. 4.33 производится очевидный выбор между потерей ферзя или слона. Но на самом деле здесь имеется лишь выбор между потерей ферзя и ферзя вместе со слоном. Ситуацию можно описать так: неизбежная потеря была отодвинута за пределы поля зрения путем менее ценной жертвы. Этот эффект обычно называют эффектом горизонта. Вторичный поиск несколько помогает, но не дает полного решения проблемы.

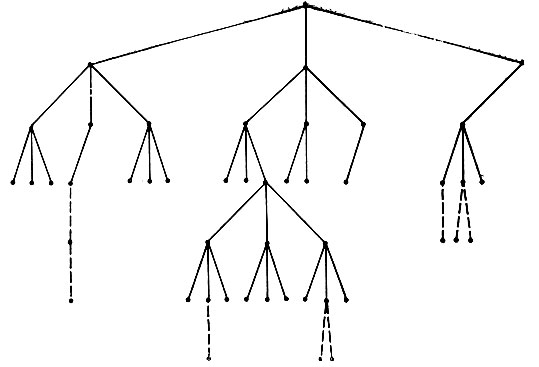
Рис. 4.32. Вторичный поиск и процедуры наращивания дерева могут вывести поиск за обычные пределы. Пунктирными линиями указаны те продолжения, которые при обычном поиске завершаются на особо динамичных ситуациях, таких, как неминуемое взятие фигуры. Небольшое продолжение, отпочковавшееся от основного дерева, проделано для того, чтобы установить статическую оценку выигрышного узла

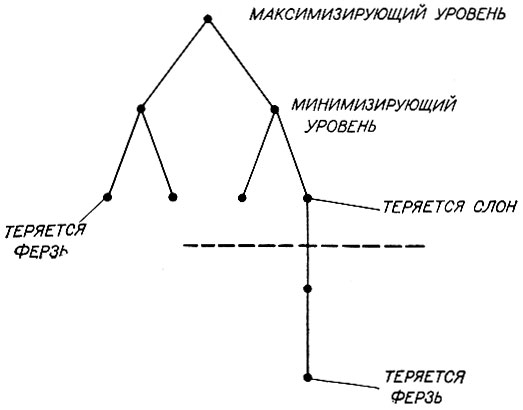
Рис. 4.33. Эффект горизонта ставит непреодолимый барьер перед игровыми процедурами, основывающимися на поиске, в тех случаях, когда катастрофу можно оттянуть, но нельзя предотвратить. Здесь ход, соответствующий левой ветви, ведет непосредственно к потере ферзя, а ход, соответствующий правой ветви, ведет к жертве, за которой следует потеря ферзя