Анализ цели-средства и универсальный решатель задач

Рассмотрим такой подход к управлению, при котором действия целиком зависят от отличия текущей ситуации от желаемой. В более специальных терминах мы представляем совокупность фактов, определяющих задачу, а также в каком положении мы в данный момент находимся, т. е. текущее состояние. Аналогично мы определяем целевое состояние. Оба они являются некоторыми совокупностями фактов, т. е. условий, накладываемых на рассматриваемый мир. Вот некоторые примеры:

• В задачах на "путешествия" текущее и целевое состояния определяются физическим местоположением.
• При решении задачи сборки с помощью робота текущее состояние может быть задано стопкой кирпичей, а целевое - некоторой построенной башней.
• При решении геометрических задач текущее состояние можно определять всем, что известно вообще и в частности для данной задачи. Целевым состоянием может быть такая же совокупность, но включающая также и то, что требовалось показать.

Представление об универсальном решателе задач опирается на некоторую стратегию выбора операторов, позволяющих уменьшить различия между текущим состоянием и целевым. Универсальный решатель задач, разработанный Ньюэллом и Саймоном, часто упоминается в литературе как GPS^* или как "анализ цели - средства".

^* (GPS - сокращение от General Problem Solver (универсальный решатель задач).- Прим. перев)

Ключевая идея состоит в работе над различиями

В случае ситуации с путешественником различие между текущим и целевым состоянием принимает особенно простую форму: это расстояние между местонахождением в данный момент и тем местом, где желательно оказаться. Рассмотрим последовательность операторов O₁,...O₅, вызывающих движение по некоторой цепочке состояний, как показано на рис. 5.1. Каждый из операторов был выбран потому, что он, как казалось, мог уменьшить различия между состоянием, к которому он применяется, и целевым состоянием. На самом деле оператор O₃ уводит нас в сторону от целевого состояния. В нашей версии системы GPS отсутствует какой-либо встроенный механизм, предотвращающий такую возможность. Хорошо, что O₄ и O₅ снова ведут в нужном направлении.

Заметим также, что ничто не препятствует переходу в состояние, у которого кажущееся расстояние до цели мало, но истинное расстояние оказывается весьма большим. Это происходит потому, что используемая мера различия часто бывает грубой, не учитывающей многие факторы, связанные с переходом из одного состояния в другое. Чтобы показать, как это просходит, представим себе альпиниста, движущегося в направлении вершины, изображенной на рис. 5.2. Если он перемещается, ориентируясь лишь на различиях в местоположении, и идет в направлении, минимизирующем это различие, то выработанный им маршрут будет проходить через расположенный на пути перевал и ему придется на него взбираться, хотя путь в обход был бы и короче, и проще.

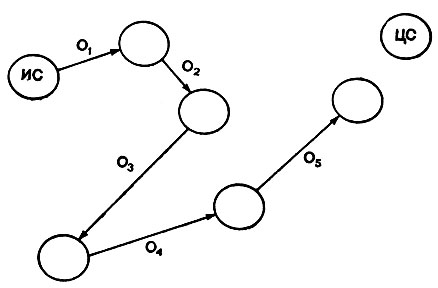
Рис. 5.1. Универсальный решатель задач - это метод, в котором выделяются состояния, различия между состояниями и операторы для уменьшения различий. Наблюдаемое различие определяет, какой оператор следует применить, но дальнейший прогресс не гарантируется

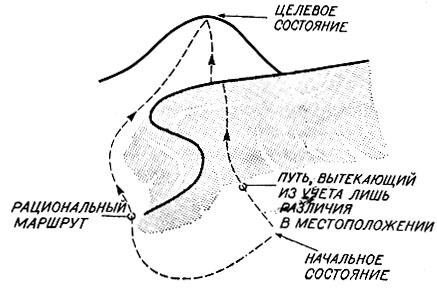
Рис. 5.2. Поскольку мера различия редко включает в себя все существенные аспекты проблемы, то универсальный решатель задач может оказаться обреченным на выбор трудных путей решения

Иногда оператор, который может уменьшить некоторое замеренное различие, не может быть использован по той причине, что для этого требуется наличие определенных характеристик, которые в текущем состоянии отсутствуют. Если этот оператор может быть применен к состоянию, расположенному рядом с текущим состоянием, то, наверное, разумно было бы перейти туда. Это иллюстрируется на рис. 5.3, где показано текущее состояние ТС, целевое состояние ЦС, различие между ними d [ТС, ЦС] и соседнее состояние СС. Соседнее состояние СС близко к текущему состоянию, но обладает тем дополнительным преимуществом, что оператор, работающий с d[ТС, ЦС], является в нем применимым.

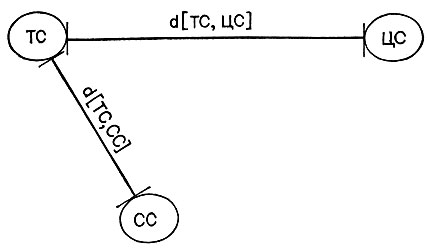
Рис. 5.3. Если различие между текущим состоянием и целевым указывает на оператор, который не может быть непосредственно применен к текущему состоянию, то может оказаться целесообразным поискать близлежащее соседнее состояние, к которому он применим. Переход в соседнее состояние представляет собой новую задачу для процедуры универсального решателя задач

Ясно, что переход к СС ничем не отличается от любой задачи прокладки пути от начального к целевому состоянию. Имеет смысл сформулировать новую задачу и заняться ею, зная, что ее решение поможет в работе над первоначальной задачей достижения ЦС. Конечно, при этом не стоило бы заниматься таким соседним состоянием, которое на самом деле находится еще дальше от целевого состояния. По этой причине оператор не рассматривается, если его условия указывают на такое соседнее состояние, для которого d [ТС, СС] > > [d ТС, ЦС].

Наконец, могут быть такие ситуации, в которых не удается найти ни одного оператора, который мог бы обеспечить движение вперед, т. е. достигается тупиковое состояние. Когда такое случается, то последний оператор отменяется и ищется новый путь, ведущий из предыдущего состояния. Эта автоматическая процедура возврата может привести к пересмотру нескольких шагов. Заметим, что процедура контроля, используемая в GPS, реализует поиск в глубину в пространстве состояний. На примере это видно яснее. Перемещение в горной местности не совсем тут подходит, и мы обратимся к несколько другой задаче, также связанной с путешествиями.

Робби отправляется в Лос-Анжелес, используя методику GPS

Тетя Агата живет в Лос-Анжелесе и приглашает Робби приехать из Бостона и провести несколько дней у нее, отдыхая на близлежащем прудике. Имеется несколько способов проделать это путешествие, и необходим некоторый критерий выбора наиболее подходящего пути в каждой точке маршрута. Расстояние, по-видимому, может служить хорошим критерием. Таблица операторов и различий позволяет связать вид путешествия с наблюдаемым расстоянием, а также сформулировать необходимые предварительные условия. См. рис. 5.4.

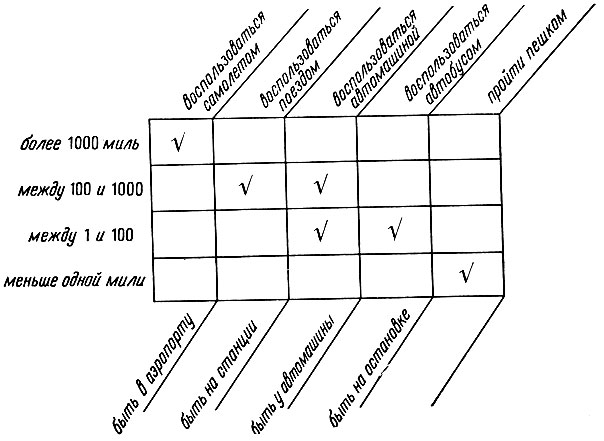
Рис. 5.4. Таблица операторов и различий показывает, какой из операторов имеет отношение к каждому из различий. Здесь изображена связь между различными транспортными возможностями и различными расстояниями,

Исходное расстояние, очевидно, превышает 1000 миль, так что таблица операторов и различий подсказывает воздушный перелет. Но предварительное условие для полета - это попасть в аэропорт, и аэропорт становится соседним состоянием, подходящим для использования оператора перелета. Таким образом, попасть в аэропорт становится промежуточной целью процесса. Расстояние меньше чем 100 миль, но больше одной мили, так что естественно воспользоваться автомобилем. При этом возникает еще одно предварительное условие, а именно оказаться на автомобильной стоянке. Для выполнения этого условия нужно пройтись пешком, что по предположению не связано ни с какими новыми предварительными условиями.

Ниже идет иллюстрация того, что мы достигли к настоящему моменту. Каждая строка смещена вправо пропорционально числу уровней, на которых возникла необходимость в удовлетворении предварительных условий.

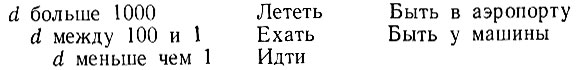
Теперь можно и что-то сделать: Робби идет к машине и едет в аэропорт. Затем перед ним вновь встает задача, как добраться до самолета, но некоторый прогресс налицо. Расстояние меньше мили, и можно пройтись пешком. Заметим, что это действие диктуется на уровне, превосходящем предыдущие.

Он идет к самолету, прилетает в аэропорт Лос-Анжелеса, а затем пытается попасть к тете Агате. Но если он последует указаниям, вытекающим из таблицы операторов и различий, то он встречается с очевидным препятствием:

Трудность, конечно, состоит в том, что первый оператор, найденный по таблице операторов и различий, связан с предварительным условием - быть у машины. Но чтобы быть у машины, необходимо совершить странное путешествие обратно в Бостон. К счастью, оно автоматически исключается договоренностью о том, что не рассматривается движение в такие соседние состояния, которые расположены дальше от цели. Поскольку когда находишься в аэропорту Лос-Анжелеса, до дома тетушки Агаты расстояние меньше, чем до своей машины, оставшейся в Бостоне, то принимается альтернатива - автобус. Остаток пути вполне очевиден:

Обычно система GPS строит цепочку к цели, а не наоборот

Во время работы GPS выбирает каждый оператор потому, что он покрывает некоторое расстояние от текущего состояния в направлении целевого состояния. Поскольку новое местоположение может оказаться все еще весьма далеким от цели, то при работе GPS может выстроиться длинная цепочка операторов, по мере того как разрабатывается дальнейший маршрут, исходя из уже достигнутого.

• Движение из начального состояния в направлении к целевому состоянию называется движением вперед.

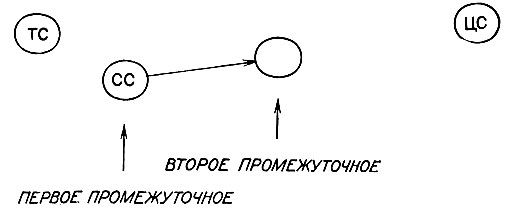
Рис. 5.5. Операторы определяют два промежуточных состояния. При работе в прямом направлении с помощью рекурсии уменьшается расстояние до первого промежуточного, или соседнего, состояния. Затем расстояние между вторым промежуточным состоянием и целью уменьшается путем применения итераций

Небольшие изменения позволяют вместо движения вперед из начального состояния рассматривать движение от целевой вершины назад. При этом, как показано на рис. 5.5, выбранный оператор на самом деле определяет два промежуточных состояния, находящихся между текущим состоянием и целевым. GPS итеративно уменьшает расстояние между вторым промежуточным состоянием и целью, в то время как на другом уровне расстояние между текущим состоянием и первым промежуточным, соседним состоянием также уменьшается. Расстояние между текущим состоянием и первым промежуточным состоянием должно быть малым.

Обращение всей процедуры создает GPS, работающий в обратном направлении, причем делается упор на сохранение малым расстояния между вторым промежуточным состоянием и целью. Итерации дают возможность заполнить пространство между исходным состоянием и первым промежуточным, а использование GPS на другом уровне позволяет заполнить пространство между вторым промежуточным состоянием и целью.

• Движение из целевого состояния в направлении к начальному состоянию называется движением назад.

Решение вопроса о том, какое движение, вперед или назад, предпочтительнее, зависит отчасти от вида пространства. На рис. 5.6 в качестве иллюстрации выступают две симметричные ситуации. Представлены все возможные состояния и операторы, переводящие состояние в соседнее. В первой из изображенных ситуаций движение вперед лучше, поскольку наблюдается определенное сужение по мере перемещения к целевым ситуациям. Трудно всерьез оказаться в тупике. Во второй ситуации предпочтительнее движение назад, так как имеется сужение в обратном направлении.

Рис. 5.6. Форма пространства состояний позволяет определить, что лучше, двигаться в прямом или в обратном направлении. Постепенное сужение говорит в пользу прямого направления, а постепенное расширение - в пользу обратного. В противном случае процедура решения будет обязательно попадать в тупики

Стратегия GPS содержит несколько эффективных идей в отношении управления

Если пойти несколько назад и посмотреть, что же делает GPS, то можно убедиться, что в этой системе использовано несколько идей.

• В GPS операторы отбираются на основе наблюдаемых различий, а не по именам.

Неявно, скорее, чем явно, выбор процедуры является ключевым моментом, тогда как использование таблицы различий и операторов - нет. Имеются и другие пути связывания различий с операторами, позволяющие обойтись без такой таблицы. Это хорошо потому, что в больших системах использование таблицы стало бы затруднительным.

• На данном уровне итерации в GPS осуществляются на основе пробной последовательности до достижения результата.

Здесь также нечто говорится о том, как выбираются процедуры. Пробно исполняемая последовательность является результатом, воплощением несколько туманной идеи обратной связи.

• При встрече с препятствиями итерации разворачиваются как поиск в глубину. Таким образом, GPS проявляет свойства автоматического возврата, представление о котором время от времени становится популярным.
• GPS применяет копии самого себя к подзадачам. Таким образом, в GPS реализуется понятие рекурсии.

Всегда, когда процедура использует копии самой себя, говорят, что она носит рекурсивный характер. На одном уровне выбор всех процедур в GPS производится на основе итерационного механизма, связанного с операторами и различиями. На другом уровне GPS вызывает себя рекурсивно и явным образом, когда встречается подзадача.

Системы редко имеют иерархически упорядоченные структуры контроля. Чаще это некоторая разнородная смесь. Правило состоит в том, чтобы пользоваться тем, что необходимо, избегая чрезмерного усложнения ради самого усложнения.

STRIPS реализация GPS

Стратегия GPS привлекательна потому, что нелегко представить себе процедуру решения задач, не включающую в себя некоторого анализа, позволяющего определить, что следует делать. Но когда используемая стратегия оказывается слишком универсальной, то между принципами и практикой может быть огромная дистанция. Знать о GPS еще не значит располагать практическим руководством. Кто-то должен решить, каким образом достаточно общие операторы, наподобие оператора "перелететь", привязываются в конкретной задаче, такой, как поездка к тетушке Ai 'е, так что при этом Робби садится на самолет, летящий в международный порт в Лос-Анжелесе, а не просто в какой угодно захолустны л аэропорт. Таким образом, кто-то должен вплотную заняться основными вопросами контроля, а именно где следует искать входные величины для процедур и как следует распоряжаться их выходами, поскольку GPS сам по себе об этом ничего не сообщает.

В Стэнфордском исследовательском институте была выполнена весьма эффектная работа на пути разработки так называемой системы STRIPS. К сожалению, для полного понимания подробностей этой системы требуется наличие определенного опыта в области автоматических процедур доказательства в исчислении предикатов. Но два проекта, построенные на основе системы STRIPS, дают важные примеры обучения и планирования. Поэтому имеет смысл заняться сейчас кратким описанием системы, хотя, быть может, подготовка некоторых читателей дала бы возможность углубиться в существо дела.

Каждый оператор в системе STRIPS состоит из трех списков фактов. Первый - список фактов, которые должны быть справедливыми (истинными), для того чтобы можно было применять этот оператор. Второй - это список фактов, которые после применения оператора перестают быть справедливыми. Эти списки называются соответственно: список предварительных условий, список изъятий (вычеркиваний) и список добавлений. Например, оператор перелета мог бы выглядеть так:

СПИСОК ПРЕДВАРИТЕЛЬНЫХ Робби в аэропорту х 
УСЛОВИИ: Имеется рейс из х в у
СПИСОК ИЗЪЯТИЙ: Робби в аэропорту х
СПИСОК ДОБАВЛЕНИЙ: Робби в аэропорту у 

Когда используется этот оператор, то мы должны уметь каким-то образом сравнивать х и у в рамках рассматриваемой задачи. Как только найден такой способ, задача обеспечения входа нашей процедуре оказывается решенной, так же как и задача выхода, поскольку списки изъятий и добавлений дают все, что для этого требуется.

Остается, однако, одна большая проблема. Это проблема учета косвенно связанных фактов. Каким образом, например, Робби узнает, что изъятие "Робби в аэропорту x" означает также изъятие "Робби в аэропорту города х". Это проблема логического вывода, которая в системе STRIPS решается с использованием системы доказательства теорем, основанной на так называемом принципе резолюции. Мы не будем здесь рассматривать эту сторону системы STRIPS по двум причинам: во-первых, для этого требуются сведения из области исчисления предикатов, а во-вторых, многие считают, что на этом принципе нельзя построить адекватную систему доказательства теорем, которая обеспечивала бы вывод, когда известных фактов больше, чем можно пересчитать по пальцам. К счастью, остальную часть системы можно вполне оценить, не обращая внимания на некоторый туман, по вопросу о том, каким образом различные списки операторов оказываются связанными с различиями, вытекающими из особенностей текущего описания мира и формулировки цели.

Запоминание последовательности операторов помогает системе решать более трудные задачи

Предположим, что STRIPS решает некоторую задачу, вырабатывая последовательность операторов О₁, ..., О_п. Рис. 5.7 иллюстрирует один из способов описания того, каким образом сохраняются в результате применения последующих операторов результаты, получаемые при действии какого-то данного оператора. Все факты, добавляемые О₁, перечислены в прямоугольнике, расположенном непосредственно под ним. Во втором прямоугольнике содержатся те же факты за вычетом фактов, которые изымаются при применении второго оператора O₂. Аналогично в третьем прямоугольнике содержатся все факты, добавляемые оператором О₁, за вычетом таких фактов, которые удаляются либо оператором O₂, либо оператором O₃.

Рис. 5.7. Таблица показывает как факты, привносимые некоторым оператором системы STRIPS, вычеркиваются последующими операторами

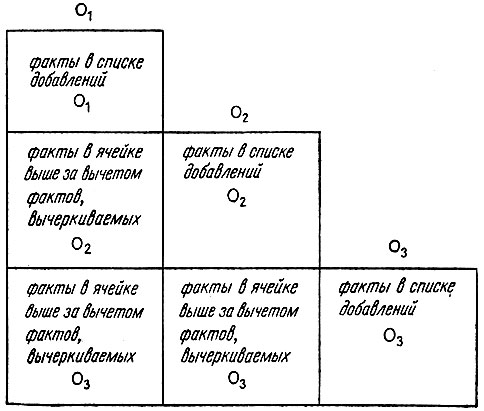
Рис. 5.8. Элементарная треугольная таблица. В каждой ее строке указаны факты, которые были добавлены и не были вычеркнуты операторами из последовательности, примененной до сих пор. Если факты какой-либо строки имеют сходство с фактами, необходимыми для достижения некоторой новой цели, то может быть использован соответствующий отрезок последовательности уже примененных операторов

Таким образом, этот рисунок показывает степень устойчивости первого оператора: остаются ли соответствующие ему добавления, или же они изымаются под действием следующих операторов с помощью треугольной таблицы. Конструкция этой таблицы имеет то свойство, что каждая ее строка содержит совокупность всех выживающих фактов, связанных с операторами, появляющимися выше. Таблица показывает, например, какие факты справедливы в результате совместного действия операторов O₁, O₂ и O₃, идущих в указанном порядке. Поскольку эти новые факты могут походить на факты, определяемые новой целью, то может оказаться разумным использовать всю последовательность О₁, O₂, O₃. Вообще говоря, ясно, что j-я строка таблицы несет некоторую информацию о том, каким образом влияют на окружающий мир первые j операторов. Если j-я строка как-то напоминает описание целевого состояния, то последовательность О₁ ..., О_j может оказаться полезной при достижении этой цели. Таким образом, треугольная таблица, построенная при решении некоторой прежней задачи, может оказаться источником последовательностей операторов, полезных при рассмотрении новых задач. Прежний план, реализующий что-то за n шагов, становится источником последовательностей операторов, применимых к n возможным целям, по одной для каждой строки. Можно было бы сказать, что последовательности операторов, таким образом, становятся супероператорами, списки добавлений которых задаются соответствующими строками треугольной таблицы.

Однако нами проделана лишь половина работы, поскольку анализ строки дает указание только относительно конца подпоследовательности. Остается еще вопрос о том, где эта последовательность начинается. Нет оснований полагать, что О₁ может быть хорошим началом. Может сложиться так, что первые несколько операторов во всей последовательности реализуют лишь то, что и так уже справедливо в рассматриваемой ситуации, поэтому лучше обратиться к последовательности операторов не с самого начала. В конечном счете наилучшей последовательностью может оказаться не O₁ ... ..., О_j, а О_i, ..., О_j.

Обнаружение подходящей начальной точки не столь простая задача, как обнаружение конечной точки. Сопоставление текущего состояния со строками не годится, потому что строки показывают не общее состояние, а лишь то, как это состояние изменилось. Лучше было бы ориентироваться на предварительные условия операторов и двигаться назад от уже найденного конечного оператора О_j к началу, остановившись там, где эти предварительные условия оказываются выполненными для некоторого оператора, который и становится искомым оператором О_i. Эта процедура не вполне совершенна, но она может послужить хорошей отправной точкой для того, чтобы понять описание корректной процедуры, которое следует ниже.

Как уже говорилось, треугольная таблица здесь не помогает, но некоторое ее расширение, изображенное на рис. 5.9, оказывается полезным. Каждый факт этой таблицы несет пометку, является ли он предварительным условием для оператора в конце строки. Всякое предварительное условие для данного оператора, которое не поставляется идущими ранее операторами, записывается в столбец слева от таблицы. Все элементы, вошедшие в этот новый левый столбец, по определению помечаются как важные предварительные условия.

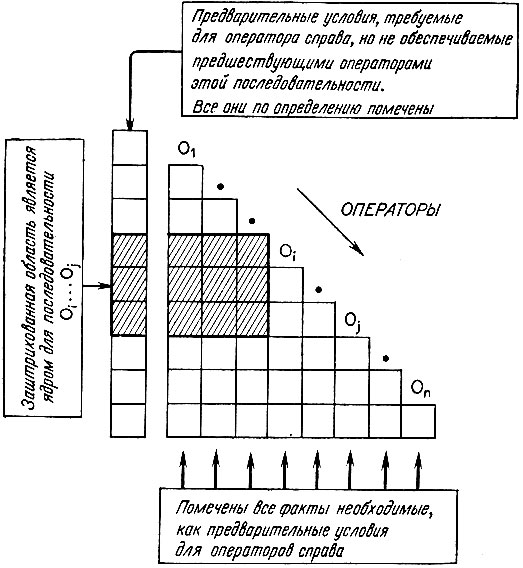
Рис. 5.9. Расширенная треугольная таблица. Все факты, которые используются в качестве предварительных условий для оператора в конце строки помечаются, а все другие предварительные условия вносятся в столбец слева. Тогда ядро последовательности операторов определяется как предварительные условия в таблице, находящиеся в прямоугольнике слева от начального оператора, простирающемся со строки начального оператора вниз до строки конечного оператора. Это ядро дает возможность системе STRIPS определять, где войти в старую последовательность операторов для достижения новой цели в свете текущей ситуации

Теперь на вопрос о том, где может начинаться последовательность операторов, можно дать четкий ответ: последовательность операторов может начаться с О_i если все факты, помеченные как предварительные условия, справедливы в прямоугольнике, расположенном влево и вниз от O_i и простирающемся вниз до заключительного оператора O_j.

Почему это так? Во-первых, ясно, что все предварительные условия для начального оператора O_i удовлетворяются, поскольку они находятся в области истинных фактов. Во-вторых, ясно, что предварительные условия для последующих операторов либо выполнены, либо будут выполнены, поскольку они либо лежат в прямоугольной области истинных фактов, расположенной влево и вниз от начального оператора, либо они будут поставляться самой последовательностью применяемых операторов по мере ее развития.

В целом способ получения подпоследовательности, относящейся к новой ситуации, на основе предыдущего плана, состоит из двух шагов:

• Во-первых, необходимо найти строку в треугольной таблице, в которой содержатся факты, напоминающие те, что характеризуют целевое описание. Оператор, расположенный в конце предыдущей строки, является заключительным в искомой последовательности.
• Затем нужно перемещаться назад по таблице от последнего, заключительного оператора до тех пор, пока не будет найден оператор, для которого все отмеченные факты слева и снизу являются истинными. Это и будет первый оператор в последовательности.

Кстати, помеченные области, соответствующие операторам, называются ядрами. Помимо того что они оказываются полезными при выборе подпоследовательностей, они оказывают существенную помощь при слежении за порядком выполнения операторов в Последовательности. Это происходит по той причине, что помеченные факты во всех ядрах должны стать истинными как раз к моменту применения соответствующих операторов. Если внешний мир неожиданным образом меняется, то некоторые факты в ядрах могут оказаться недействительными, приводя, таким образом, к конфликту с условиями истинности для ядер и заставляя устройство, выполняющее операторы, приостановить работу.

Учет рекурсий придает системе STRIPS возможности планировщика

Иногда решение некоторой задачи может быть связано с глубокой рекурсией и большими затратами, связанными с попыткой удовлетворения предварительных условий. Поэтому следует уделить особое внимание тому, чтобы избегать работы над какими-либо предварительными условиями для следующего шага, если еще до того, как удалось выполнить все предварительные условия, стало ясно, что этот шаг плох.

Сейсердоти развил метод, позволяющий автоматически избегать работы по удовлетворению предварительных условий на некотором шаге в тех случаях, когда этот шаг по прогнозу оказывается неудачным. Основная идея состоит в получении наброска решения до того,

как будут уточнены отдельные детали. Некоторая форма планирования при этом обеспечивается, если временно игнорировать необходимость выполнения предварительных условий. Для иллюстрации предположим, что приближается суббота, Робби находится в Лос-Анжелесе и пора позаботиться о том, как провести свободное время. Целью становится организация свидания, причем следующие предварительные условия имеют к этой цели отношение:

• Мэри увлекается теннисом → следует договориться о корте и запастись новыми мячами.
• Марта любит ходить в роскошные рестораны → необходимо отнести вечерний костюм в срочную химчистку.
• Маргарета помешана на велосипеде → необходимо где-то достать на время второй велосипед.

Здесь ясно, что много усилий будет затрачено впустую, если заниматься предварительными условиями до того, как будет проверена выполнимость основного шага. Было бы глупо заботиться о теннисном корте, если девушка заведомо занята. Все, что нужно, вообще говоря, это позвонить по телефону, чтобы узнать имеет ли смысл заниматься предварительными условиями^*.

^* (Приведенный пример является уместным, только если выполнение предварительных условий в принципе гарантировано. Если же они сами, например, могли составить трудную подзадачу, то Робби с его "широкими взглядами" мог бы, наоборот, поставить выбор девушки в зависимости от того, что ему легче сделать - доставать себе велосипед или отдать костюм в чистку.- Прим. перев.)

В примере, относящемся к тетушке Агате, предварительные условия для самого первого шага, попасть на самолет, связаны с некоторым объемом рекурсивного решения задач, хотя и не очень большим. Все же идею Сейсердоти на этом примере проиллюстрировать можно.

Смысл упомянутой рекурсии может быть пояснен с помощью схемы на рис. 5.10, где по вертикали отложена рекурсивная глубина, а по горизонтали - ход времени. На самом деле это просто некоторое отражение предыдущей диаграммы. В этой новой форме рекурсия видна яснее, так как центр активности перемещается вниз каждый раз, когда предварительные условия заставляют работать над подзадачами, и вверх, когда с некоторой подзадачей покончено. Разумеется, показанное время не соответствует реально затрачиваемому времени.

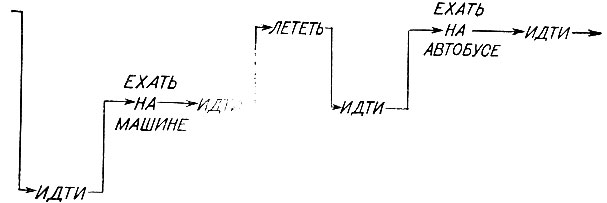
Рис. 5.10. В универсальном решателе задач может быть использована глубокая рекурсия для того, чтобы подготовиться к применению оператора имеющего отношение к главной цели. Здесь один оператор третьего уровня и два оператора второго уровня подготавливают применение оператора первого уровня ЛЕТЕТЬ

При поездке к тетушке Агате используется два уровня планирования. Активность на каждом уровне можно представлять себе в виде некоторого упражнения по планированию, причем детали будут выясняться в результате работы, проделанной на уровень ниже. Сначала задача решается на верхнем уровне лишь главных шагов - вопросом приезда в аэропорт интересоваться не надо, пока не будут изучены последствия такого шага. Как показано на рис. 5.11, промежутки заполняются позже, после того как станет очевидным успех главного предприятия. Но при их заполнении опять никакого внимания не уделяется предварительным условиям. Задача добраться до машины откладывается до третьего цикла.

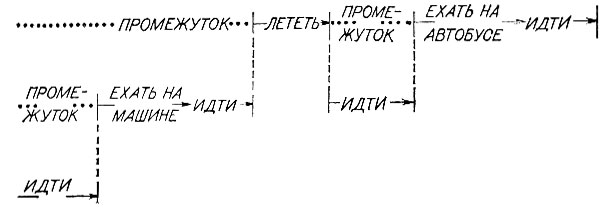
Рис. 5.11. В реализации универсального решателя задач в форме системы STRIPS удается избежать напрасных усилий, связанных с подготовкой к использованию неудачных операторов высших уровней, путем откладывания проведения рекурсий, связанных с необходимыми предварительными условиями. Результатом является нечто, что может быть названо поиском в длину. Здесь первым делом проверяется, достигают ли операторы высшего уровня поставленной цели. Затем исследуются задачи второго уровня, связанные с предварительными условиями, при этом опять откладывается рассмотрение деталей. Наконец, остающиеся промежутки заполняются на третьем проходе

Почему нужны все эти сложности? В приведенном примере этот подход не дает каких-либо преимуществ, поскольку, как только некоторый оператор фиксировался, он оказывался и полезным, и правильным. Но если имеется возможность выбора среди нескольких операторов, каждый из которых имеет хорошие, но не очевидные шансы на успех, то, несомненно, система решения задач должна стараться избегнуть напрасных усилий по удовлетворению предварительных условий для некоторого оператора, если он окажется неудачным.